3.1 The Floating-Point Formats
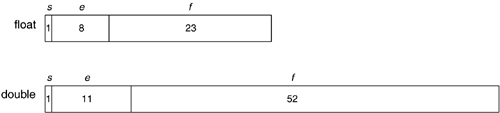
3.1 The Floating-Point Formats Before the IEEE 754 standard was published in 1985, there were many different floating-point formats which the computer manufacturers implemented in hardware and software. It was difficult to port programs that did numerical computations from one machine platform to another the computed results would vary. Most computer hardware manufacturers today adhere to the IEEE 754 standard, and to various degrees software, such as language compilers, supports the standard's features. The standard specifies number formats, operations, conversions, and exceptions. Number formats refer to how the numbers are encoded in memory. Java's two primitive types float and double conform to the standard's 32-bit single-precision format and the standard's 64-bit double-precision format, respectively. Each format breaks a number into three parts : a sign bit, an exponent, and a fraction. The two formats differ in the number of bits allocated to the exponent and fraction parts. Figure 3-1 shows the layouts of the single-precision and double-precision formats, with the bit sizes of each part. In both formats, the most significant bits of the exponent and of the fraction are at their left ends. Figure 3-1. The layouts of the single-precision float and double-precision double number formats. The numbers are the bit sizes of each of the parts. The sign bit represents the sign of the number value: 0 for positive and 1 for negative. The exponent is unsigned, and so it is always positive. To allow it to represent negative exponent values, the standard adds a positive bias. We call this a biased exponent. To get the unbiased (true) value of the exponent, we must subtract off the bias. In the single-precision format, the exponent is 8 bits. It can store the biased values 0 through 255, but 0 and 255 are reserved. The bias is 127, and so the unbiased exponent values are -126 through +127. In the double-precision format, the exponent is 11 bits. It can store the biased values 0 through 2047, but 0 and 2047 are reserved. The bias is 1023, and so the unbiased exponent values are -1022 through +1023. We can use the fraction part to calculate the floating-point number's value v. Let s be the value of the sign bit, e be the biased exponent value, E be the unbiased exponent value, and f be the fraction value. Normalized NumberIf the e is not a reserved value (0 and 255 for float, or 0 and 2047 for double ), then there is an implied 1 bit followed by an implied binary point just to the left of f' s first bit. Move the implied point to the right or left E bit positions (depending on whether E is positive or negative, respectively) to get the number's absolute value, and s determines whether the value is positive or negative (0 for positive, 1 for negative): This is a normalized number. The implied bit, the implied point, and the fraction constitute a number's significand, so a single-precision number has 24 bits in its significand, and a double-precision number has 53 bits in its significand. For a float example, let Then and the significand is binary 1.10000000000000000000000 after we append the implied 1 bit and the implied binary point. If we move the binary point two places left, the value in binary is 0.011, which is The maximum positive float value has Then and the significand is binary 1.11111111111111111111111. The value is If we set s = 1, we get the most negative value, which is approximately -3.4 x 10 38 . Denormalized Number If e = 0 (one of the reserved values) and f and For a float example, let and the significand is binary 0.00101000000000000000000 after we insert the implied 0 bit and the implied binary point. We move the binary point 126 to the left, and we get the value The minimum positive float value has and the significand is binary 0.00000000000000000000001. The value is If s = 1, the minimum negative float value is approximately -1.4 x 10 - 45 . There are several special cases to implement some constant values:
For example, dividing 0 by 0 results in NaN. Table 3-1. Summary of Java's float and double formats.
This is all quite messy, but fortunately, the Java virtual machine takes care of all of it automatically. Table 3-1 summarizes the two formats. |
| |
| Top |
EAN: 2147483647
Pages: 141


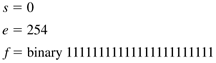
 0, then we have a
0, then we have a 
