14.3 Fluent Linear Temporal Logic (FLTL)

14.3 Fluent Linear Temporal Logic (FLTL)

In the previous section, we saw the use of the always [] operator to express safety properties and the use of the eventually operator <> to express liveness properties. These represent by far the most common use of linear temporal logic in expressing properties. In the following, we complete the description of our fluent linear temporal logic (FLTL) by describing the remaining operators – until U, weak until W and next time X.

14.3.1 Until

The linear temporal logic formula p U q is true if and only if q is true at the current instant or if q is true at some instant in the future and p is true until that instant.

For example, suppose we wish to assert the politeness property of Chapter 7 that we should not enter a room before knocking. We can assert:

 assert POLITE = (!enter U knock)

This asserts both the safety property that we cannot have an enter action before a knock action, and also that a knock action should eventually happen. This can be seen clearly from the Büchi automaton for this property depicted in Figure 14.6. The automaton irretrievably enters the acceptance state 1 if an enter action occurs before a knock action occurs. However, if a knock action never occurs, the property is violated because the automaton remains in state 0 which is also an acceptance state.

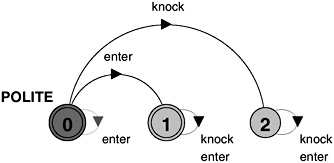
Figure 14.6: POLITE Büchi automaton.

Given the until operator, we can state the mutual exclusion property of section 14.2.1 using only action fluents:

 assert MUTEX_U = []((p[1].enter -> (!p[2].enter U p[1].exit))                   &&(p[2].enter -> (!p[1].enter U p[2].exit)))

This expresses the required mutual exclusion safety property and, in addition, the liveness property that if a process enters the critical section it should eventually exit. However, the property is considerably more complex than that of section 14.2.1 and is difficult to extend to more than two processes.

14.3.2 Weak Until

The linear temporal logic formula p W q is true if and only if either p is true indefinitely or if p U q.

The difference with the previous definition of until is that this definition does not insist that q eventually happens. The formula also holds if p is true indefinitely. This means that if we use weak until for the POLITE property:

 assert POLITE_W = (!enter W knock)

the property becomes a safety property since it no longer requires that knock eventually happens. The safety property is depicted in Figure 14.7.

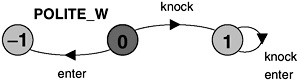
Figure 14.7: POLITE_W safety property process.

In the same way, if we replace until with weak until in the definition of the mutex property, it becomes a safety property which generates exactly the same automaton as that depicted in Figure 14.1.

 assert MUTEX_W = []((p[1].enter -> (!p[2].enter W p[1].exit))                   &&(p[2].enter -> (!p[1].enter W p[2].exit)))

In general, there is no need to distinguish between safety and liveness properties when using FLTL to specify properties. Since the safety check is more efficient than the connected component search used in checking general FLTL properties, the LTSA generates a safety property process if it detects that a property is only a safety property. In fact, determining whether a Büchi automaton can be transformed to a safety property process is non-trivial and the LTSA does not guarantee to perform this transformation for all automata that could be reduced.

It should be noted that we could have specified the liveness property that was included in MUTEX_U in the original MUTEX_N property as follows:

 assert EXIT_N = forall[i:1..N][](p[i].enter -> <>p[i].exit) assert MUTEX_LIVE = (MUTEX_N && EXIT_N)

MUTEX_LIVE expresses the same property for N processes that MUTEX_U does for two. In fact we can parameterize assertions as follows:

 assert MUTEXP(M=2)     = []!(exists [i:1..M-1] (CRITICAL[i] && CRITICAL[i+1..M])) assert EXITP(M=2)     = forall[i:1..M] [](p[i].enter -> <>p[i].exit) assert MUTEX_LIVEP(P=2)     = (MUTEXP(P) && EXITP(P))

Definitions

We can define the temporal operators always [], eventually <> and weak until W in terms of the until U operator as follows:

 <> p ≡ True U p [] p ≡ !<>!p p W q ≡ []p || (p U q) 

In fact, FLTL does not have the explicit constants True and False; instead it permits boolean expressions of constants and parameters. These expressions are termed “rigid”, since, unlike fluent propositions, they do not change truth value with the passage of time as measured by the occurrence of events. Thus we can define:

 assert True  = rigid(1) assert False = rigid(0)

Rigid expressions can be used in conjunction with parameters and ranges and are essentially used to introduce boolean expressions into FLTL formulae, e.g.

 assert Even(V=3) = rigid(V/2 == 0)

14.3.3 Next Time

The linear temporal logic formula X p is true if and only if p is true at the next instant.

By “next instant” in the above definition, we mean when the next action occurs – this includes silent actions. For example, the assertion:

 assert SEQ = (a && X b && X X c)

requires that in the initial instant of system execution the action a occurs followed by the action b, followed by the action c. To check for this sequence, the property process shown in Figure 14.8 is generated:

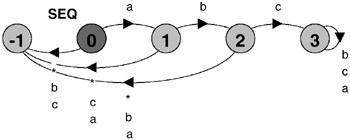
Figure 14.8: SEQ property process.

In fact, this form of property is not very useful. If we were to refine or extend our system (using, say, parallel composition and interleaving) such that actions could occur inbetween a, b or c then the property would no longer hold. This is because next time refers to precisely the time at which the next action occurs, whether silent or not. Consequently, it makes finer distinctions than the observational equivalence that is preserved when we minimize processes. As such, it is rarely used in property specification. In addition, it can prohibit the use of partial order reduction, a technique that can dramatically reduce the time taken to check an FLTL property.