2.6. The (Axis-Parallel BoxAxis-Parallel Box) Windowing Problem

2.6. The (Axis-Parallel Box/ Axis-Parallel Box) Windowing Problem

We consider the problem of answering the following (axis-parallel box/axis-parallel box) windowing query. For a set of rectangular boxes, we want to find all boxes that are intersected by a query box B :

• Input: a set S of rectangular boxes in 2D;

• Query: a rectangular box B in 2D;

• Output: all boxes of S that intersect with B .

Let us assume that a set S of n rectangular boxes B ₁ , B ₂ , , B _n is given. A rectangular box B _i has points inside B in the following three cases (see Figure 2.9):

• The query B is fully contained in B _i ;

• An endpoint of B _i lies inside B ;

• A segment of B _i crosses B , and no endpoint of B _i is inside B .

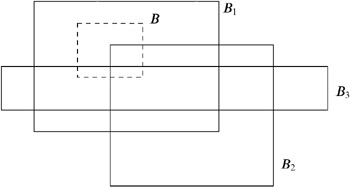
Figure 2.9: The box B _i reported by a (axis-parallel box/axis-parallel box) windowing query for B contains B for i = 1, has a vertex inside B for i = 2, and has a segment that crosses B for i = 3.

For the first case, we can use a 2D segment tree of the boxes of S ; see Section 2.3. We answer (axis-parallel box/point) stabbing queries for the four end-points of B . These operations require O ( k ₁ + log ² n ) time and O ( n + log ² n ) space, where k ₁ denotes the number of boxes in S that fully contain B .

In the second case, we can use a range tree in 2D and answer a rectangular (point/axis-parallel box) windowing query for the endpoints of the B _i s with respect to B ; see Section 2.5. This can be performed in time O ( k ₂ + log ² n ) and O ( n log n ) space, where k ₂ denotes the number boxes B _i with endpoints in B .

The third case cannot be solved directly with the former approaches. We have to answer the following (horizontal line segment/vertical line segment) stabbing query for the vertical line segments of box B and the horizontal line segments of all boxes B _i for i = 1 , , n .

• Input: a set S of horizontal line segments in 2D;

• Query: a vertical line segment s in 2D;

• Output: all segments of S intersected by s .

Of course, we have to answer also a (vertical line segment/horizontal line segment) stabbing query. This is done by a simple rotation of 90 degrees.

A subset of horizontal line segments of S is stabbed by the line passing through the vertical line segment s . Obviously, among these line segments, we must report all line segments whose left endpoints lie in a rectangular range grounded in s and going to ˆ ; see Figure 2.10. If s is given by ( x, y _l ) and ( x, y _u ), the corresponding box is represented by [ ˆ ˆ , x ] — [ y _l , y _u ].

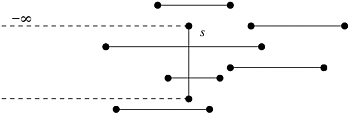
Figure 2.10: A rectangular range query by an infinite box grounded in s will answer the windowing query in the third case.

Now, we have a stabbing query and a range query, and we adapt an interval tree accordingly . The horizontal segments of S are stored in an interval tree for the x -coordinates of the segments. We have to report the horizontal segments h stabbed by the x -coordinate x of s . For the left endpoints of such a segment h , we have to take care that the y -coordinate of h lies also in the interval [ y _l , y _u ]. A node v of a regular interval tree contains the list S _med of the segments hit by x _med ; see Section 2.1. We replace the sorted list M _L and M _R of the left and right endpoints of S _med by two range trees. A 2D range tree M _L for the left endpoints of the segments in S _med and a 2D range tree M _R for the right endpoints of the segments in S _med .

In Algorithm 2.1, we simply replace

with

This gives an additional log factor for the space of the structure. For an interval query and a node v , it suffices to check the corresponding 2D range trees. Note that all segments in S _med are crossed by the line X = x _med . For example, if x < x _med , we use the range tree M _L of the left endpoints of S _med ; see Figure 2.11. We answer the range query for [ y _l , y _u ] — [ ˆ ˆ , x ]. Algorithm 2.2 is extended in a straightforward manner.

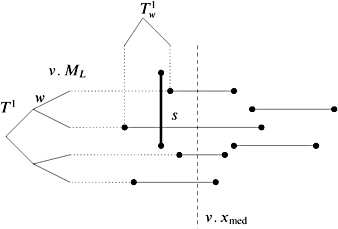
Figure 2.11: At the node v with a median v. x _med in an interval tree, there is also a 2D range tree v. M _L of the left endpoints of the segments in v. S _med . v. M _L answers the query [y _l , y _u ] — [ ˆ ˆ , x] for a segment s = [(x, y _l ), (x, y _u )].

In time O (log n + k _v ), we can report the k _v segments of S _med at node v that hit s and go on with the left children and L _med in the interval tree query. Altogether, we traverse log n nodes and report all k intersecting segments, which gives O ( k + log ² n ) query time.

With the results from the previous section, we can construct the extended interval tree in O ( n log n ) with O ( n log n ) space.

Theorem 2.14. A 2D (axis-parallel box/axis parallel box) windowing query can be answered in O (log ² + k ) time where k denotes the number of reported boxes. The corresponding data structures require O ( n log n ) space and are built up in O ( n log n ) time.

As a subresult, we have shown how to report all horizontal line segments that are crossed by a single vertical line segment.

Theorem 2.15. A (horizontal line segment/vertical line segment) stabbing query can be answered in O (log ² + k ) time, where k denotes the number of reported line segments. The corresponding data structures require O ( n log n ) space and are built up in O ( n log n ) time.

A WeakDelete operation for the combined interval range tree can be done in O (log ² n ) time, since we additionally have to make a WeakDelete in the 2D range tree.

Lemma 2.16. A WeakDelete operation for the combined interval range tree for n boxes in 2D can be performed in O (log ² n ) time.