Introduction to Probability and Statistics for Projects
Lies, damned lies, and statistics!
"Nothing in progression can rest on its original plan."Thomas Monson
There are No Facts about the Future
"There are no facts about the future!" This is a favorite saying of noted risk authority Dr. David T. Hulett that sums it up pretty well for project managers. [1] Uncertainty is present in every project, every project being a unique assembly of resources and scope. Every project has its ending some time hence. Time displaces project outcomes from the initial estimates; time displacement introduces the opportunity for something not to go according to plan. Perhaps such an opportunity would actually have an upside advantage to the project, or perhaps not. Successful project managers are those quick to grasp the need for the means to evaluate uncertainty. Risk management is the process, but probability and statistics provide the mathematical underpinning for the quantitative analysis of project risk. Probability and statistics for project managers are the subjects of this chapter.
[1]The author has had a years-long association with Dr. Hulett, principal at Hulett Associates in Los Angeles, California. Among many accomplishments, Dr. Hulett led the project team that wrote the "Project Risk Management" chapter of the 2000 edition of A Guide to the Project Management Body of Knowledge, published by the Project Management Institute.
Probability What Do We Mean by It?
Everyone is familiar with the coin toss — one side is heads, the other side is tails. Flip it often enough and there will be all but an imperceptible difference in the number of times heads comes up as compared to tails. How can we use the coin toss to run projects? Let us connect some "dots."
Coin Toss 101
As an experiment, toss a coin 100 times. Let heads represent one estimate of the duration of a project task, say writing a specification, of 10 days, and let tails represent an estimate of duration of 15 days for the same task. Both estimates seem reasonable. Let us flip a coin to choose. If the coin were "fair" (that is, not biased in favor of landing on one side or the other), we could reasonably "expect" that there would be 50 heads and 50 tails.
But what of the 101st toss? What will it be? Can we predict the outcome of toss 101 or know with any certainty whether the outcome of toss 101 will be heads or tails, 10 days duration or 15? No, actually, the accumulation of a history of 50 heads and 50 tails provides no information specifically about outcome of the 101st toss except that the range of possible performance is now predictable: toss 101 will be either discretely heads or tails, and the outcome of toss 101 is no more likely to come up heads than tails. So with no other information, and only two choices, it does not matter whether the project manager picks 10 or 15 days. Both are equally likely and within the predicted or forecast range of performance. However, what of the next 100 tosses? We can reasonably expect a repeat of results if no circumstances change.
The phenomenon of random events is an important concept to grasp for applications to projects: the outcome of any single event, whether it be a coin toss or a project, cannot be known with certainty, but the pattern of behavior of an event repeated many times is predictable.
However, projects rarely if ever repeat. Nonrepetitiveness is at the core of their uncertainty. So how is a body of mathematics based on repetition helpful to project managers? The answer lies in how project managers estimate outcomes and forecast project behavior. We will see the many disadvantages of a "single-point" estimate, sometimes called the deterministic estimate, and appreciate the helpfulness of forecasting a reasonable range of possibilities instead. In the coin toss, there is a range of possible outcomes, heads or tails. If we toss the coin many times, or simulate the tossing of many times, we can measure or observe the behavior of the outcomes. We can infer (that is, draw a conclusion from the facts presented) that the next specific toss will have similar behavior and the outcome will lie within the observed space. So it is with projects. From the nondeterministic probabilistic estimates of such elements as cost, schedule, or quality errors, we can simulate the project behavior, drawing an inference that a real project experience would likely lie within the observed behavior.
Calculating Probability
Most people would say that the probability of an outcome of heads or tails in a fair coin toss is 50%; some might say it is half, 0.5, or one chance in two. They all would be correct. There is no chance (that is, 0 probability) that neither heads nor tails will come up; there is 100% probability (that is, 1) that either heads or tails will come up.
What if the outcome was the value showing on a die from a pair of dice that was rolled or tossed? Again most people would say that the probability is 1/6 or one chance in six that a single number like a "5" would come up. If two dice were tossed, what is the chance that the sum of the showing faces will equal "7"? This is a little harder problem, but craps players know the answer. We reason this way: There are 36 combinations of faces that could come up with the repetitive roll of the die, like a "1" on both faces (1,1) or a "1" on one face and a "3" on the other (1,3). There are six combinations that total "7" (1,6; 6,1; 2,5; 5,2; 3,4; 4,3) out of a possible 36, so the chances of a "7" are 6/36 or 1/6.
The probability that no combination of any numbers will show up on a roll of the dice is 0; the probability that any combination of numbers will show up is 36/36, or 1. After all, there are 36 ways that any number could show up. Any specific combination like a (1,6) or a (5,3) will show up with probability of 1/36 since a specific combination can only show up one way. Finally, any specific sum of the dice will show up with probability between 1/36 and 6/36. Table 2-1 illustrates this opportunity space.
|
Combination Number |
Face Value #1 |
Face Value #2 |
Sum of Face Values |
|---|---|---|---|
|
1 |
1 |
1 |
2 |
|
2 |
2 |
1 |
3 |
|
3 |
3 |
1 |
4 |
|
4 |
4 |
1 |
5 |
|
5 |
5 |
1 |
6 |
|
6 |
6 |
1 |
7 |
|
7 |
1 |
2 |
3 |
|
8 |
2 |
2 |
4 |
|
9 |
3 |
2 |
5 |
|
10 |
4 |
2 |
6 |
|
11 |
5 |
2 |
7 |
|
12 |
6 |
2 |
8 |
|
13 |
1 |
3 |
4 |
|
14 |
2 |
3 |
5 |
|
15 |
3 |
3 |
6 |
|
16 |
4 |
3 |
7 |
|
17 |
5 |
3 |
8 |
|
18 |
6 |
3 |
9 |
|
.... |
.... |
.... |
.... |
|
36 |
6 |
6 |
12 |
|
Notes: The number "7" is the most frequent of the "Sum of Face Values," repeating once for each pattern of 6 values of the first die, for a total of 6 appearances in 36 combinations. |
|||
|
Although not apparent from the abridged list of values, the number "5" appearing in the fourth-down position in the first pattern moves up one position each pattern repetition and thus has only 4 total appearances in 36 combinations. |
|||
Relative Frequency Definitions
The exercise of flipping coins or rolling dice illustrates the "relative frequency" view of probability. Any specific result is an "outcome," like rolling the pair (1,6). The six pairs that total seven on the faces are collectively an "event." We see that the probability of the event "7" is 1/6, whereas the probability of the outcome (1,6) is 1/36. All the 36 possible outcomes are a "set," the event being a subset. "Population" is another word for "set." "Opportunity space" or sometimes "space" is used interchangeably with population, set, subset, and event. Context is required to clarify the usage.
The relative frequency interpretation of probability leads to the following equation as the general definition of probability:
p(A) = N(A)/N(M)
where p(A) is probability of outcome (or event) A, N(A) = number of times A occurs in the population, and N(M) = number of members in the population.
AND and OR
Let's begin with OR. Using the relative frequency mathematics already developed, what is the probability of the event "5"? There are only four outcomes, so the event "5" probability is 4/36 or 1/9.
To make it more interesting, let's say that event "5" is the desired result of one of two study teams observing the same project problem in "dice rolling." One team we call study team 5; the other we call study team 7. We need to complete the study in the time to complete 36 rolls. Either team finishing first is okay since both are working on the same problem. The probability that study team 5 will finish its observations on time is 4/36. If any result other than "5" is obtained, more time will be needed.
Now let's expand the event to a "5" or a "7". Event "7" is our second study team, with on-time results if it observes a "7". Recall that there are six event "7" opportunities. There are ten outcomes between the two study teams that fill the bill, giving either a "5" or a "7" as the sum of the two faces. Then, by definition, the probability of the event "5 OR 7" is 10/36. The probability that one or the other team will finish on time is 10/36, which is less risky than depending solely on one team to finish on time. Note that 10/36 is the sum of the probabilities of event "7" plus event "5": 6/36 + 4/36 = 10/36. [2]
It is axiomatic in the mathematics of probability that if two events are mutually exclusive, then when one occurs the other will not:
p(A OR B) = p(A) + p(B)
Now let's discuss AND. Consider the probability of the schedule event "rolling a 6 on one face AND rolling a 1 on the other face." The probability of rolling a "6" on one die is 1/6, as is the probability of rolling a "1" on the other. For the event to be true (that is, both a "6" and a "1" occur), both outcomes have to come up. Rolling the first die gives only a one-in-six chance of a "6"; there is another one-in-six chance that the second die will come up "1", altogether a one-in-six chance times a one-in-six chance, or 1/36. Of course 1/36 is very much less than 1/6. If the outcomes above were about our study teams finishing on time, one observing for a "6" on one die and the other observing for a "1" on the other die, then the probability of both finishing on time is the product of their individual probabilities. Requiring them both to finish on time increases the risk of a joint on-time finish event. We will study this "merge point" event is more detail in the chapter on schedules.
Another axiom we can write down is that if two events are independent, in no way dependent on each other, then:
p(A AND B) = p(A * B) = p(A) * p(B)
AND and OR with Overlap or Collisions
We can now go one step further and consider the situation where events A and B are not mutually exclusive (that is, A and B might occur together sometimes or perhaps overlap in some way). Figure 2-1 illustrates the case. As an example, let's continue to observe pairs of dice, but the experiment will be to toss three die at once. All die remain independent, but the occurrence of the event "7" or "5" is no longer mutually exclusive. The event {3,4,1} might be rolled providing the opportunity for the (3,4) pair of the "7" event and the (4,1) pair of the "5" event. However, we are looking for p(A) or p(B) but not p(A * B); therefore, those tosses like event {3,4,1} where "A and B" occur cannot be counted, thereby reducing the opportunities for either A or B. Throwing out the occurrence of "A and B" reduces the chances for "A or B" alone to happen. From this reasoning comes a more general equation for OR:
p(A OR B) = p(A) + p(B) - p(A * B)

Figure 2-1: Overlapping Events.
Notice that if A and B are mutually exclusive, then p(A * B) = 0, which gives a result consistent with the earlier equation given for the OR situation.
Looking at the above equation, the savvy project manager recognizes that risk has increased for achieving a successful outcome of either A or B since the possibility of their joint occurrence, overlap, or collision of A and B takes away from the sum of p(A) + p(B). Such a situation could come up in the case of two resources providing inputs to the project, but if they are provided together, then they are not useful. Such collisions or race conditions (a term from system engineering referring to probabilistic interference) are common in many technology projects.
Conditional Probabilities
When A and B are not independent, then one becomes a condition on the outcome of the other. For example, the question might be: What is the probability of A given the condition that B has occurred? [3]
Consider the situation where there are 12 marbles in a jar, 4 black and 8 white. Marbles are drawn from the jar one at a time, without replacement. The p(black marble on first draw) = 4/12. Then, a second draw is made. Conditions have changed because of the first draw. There are only 3 black marbles left and only 11 marbles in the jar. The p(black marble on the second draw given a black marble on the first draw) = 3/11, a slightly higher probability than 4/12 on the first draw. The probability of the second draw is conditioned on the results of the first draw.
The probability of a black marble on each of the first two draws is the AND of the probabilities of the first and second draw. We write the equation:
p(B and A) = p(B) * p(A | B)
where B = event "black on the first draw," A = event "black on second draw, given black on first draw," and the notation "|" means "given." Filling in the numbers, we have:
p(B and A) = (4/12) * (3/11) = 1/11
Consider the project situation given in Figure 2-2. There we see two tasks, Task 1 and Task 2, with a finish-to-start precedence between them. [4] The project team estimates that the probability of Task 1 finishing at the latest finish of "on time + 10 days" is 0.45. Task 1 finishing is event A. The project team estimates that the probability of Task 2 finishing on time is 0.8 if Task 1 finishes on time, but diminishes to 0.4 if Task 1 finishes in "on time + 10 days." Task 2 finishing is event B. If event A is late, it overlaps the slack available to B. We calculate the probability of "A * B" as follows:
p(A10 * B0) = p(B0 | A10) * p(A10) = 0.4 * 0.45 = 0.18
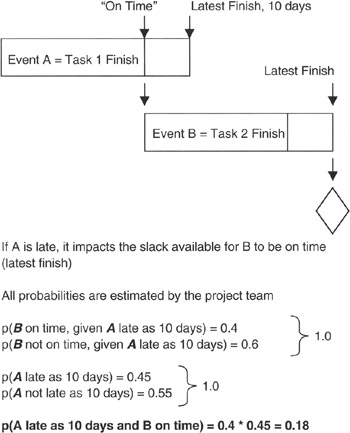
Figure 2-2: Conditions in Task Schedules.
where A10 = event of Task 1 finishing "on time + 10 days" and B0 = event of Task 2 finishing on time if Task 1 finishes "on time + 10 days." Conclusion: there is less than one chance in five that both events A10 and B0 will happen. The project manager's risk management focus is on avoiding the outcome of B finishing late by managing Task 1 to less than "on time + 10 days."
There is a lot more to know about conditional probabilities because they are very useful to the project manager in decision making and planning. We will hold further discussion until Chapter 4, where conditional probabilities will be used in decision trees and tables.
The (1 p) Space
To this point, we have been using a number of conventions adopted for probability analysis:
- All quantitative probabilities lie in the range between the numbers 0 (absolute certainty that an outcome will not occur) and 1 (absolute certainty that an outcome will occur).
- The lower case "p" is the notation for probability; it stands for a number between 0 and 1 inclusively. Typically, "p" is expressed as a decimal.
- If "p" is the probability that project outcome A will happen, then "1-p" is the probability that project outcome A will not occur. We then have the following equation: p + (1-p) = 1 at all times. More rigorously, we write: p(A) + [1-p(A)] = 1, where the notation p(A) means "probability that A will occur."
- "1-p" is the probability that something else, say project outcome B, will happen instead of A. After all, there cannot be a vacuum in the project for lack of outcome A. Sometimes outcome B is most vexing for project managers. B could well be a "known unknown." To wit: Known...A may not happen, but then unknown...what will happen, what is B?
- Sometimes it is said: B is in the (1-p) space of A, or the project manager might ask his or her team: "What is in the (1-p) space of A?"
- Project managers must always account for all the scope and be aware of all the outcomes. Thus: p(A) + p(B) = 1. A common mistake made by the project team is to not define or identify B, focusing exclusively on A.
Of course, there may be more possibilities than just B in the (1-p) space of A. Instead of just B, there might be B, C, D, E, and so forth. In that case, the project manager or risk analyst must be very careful to obey the following equation:
[1-p(A)] = p(B) + p(C) + p(D) + p(E) + ...
The error that often occurs is that the right side sums up too large. That is, we have the condition:
p(A) + p(1-A) > 1
On the right side, there are either too many possibilities identified, their respective probabilities are too large, or on the left side, the probabilities of A are misjudged. It is left to the project team to recognize the error of the situation and take corrective measures.
Subjective Probability
What about statements like "there is a 20% chance of rain or snow today in the higher elevations"? A statement of this type does not express a relative frequency probability. We do not have an idea of the population (number of times it rains or snows in a time period), so there is no way to see the proportionality of the outcome to the total population. Statements of this type, quite commonly made, express a subjective notion of probability. We will see that statements of this type express a "confidence." We arrive at "confidence" by accumulating probabilities over a range. We discuss more about "confidence" later.
[2]In the real world, events "5" and "7" could be the names given to two events in a "tree" or hierarchy of events requiring study. For example, events "5" and "7" could be error conditions that might occur. Rolling the dice is equivalent to simulating operational performance. Dr. David Hulett suggested the fault tree to the author.
[3]A might be one approach in a project and B might be another approach. Such a situation comes up often in projects in the form of "if, then, else" conditional branching.
[4]A finish-to-start precedence is a notation from precedence diagramming methodology. It denotes the situation that the finish of the first task is required before the start of the second (successor) task can ensue. It is often referred to as a "waterfall" relationship because, when drawn on paper, it gives the appearance of a cascade from one task to the other. More on critical path scheduling can be found in Chapter 6 of A Guide to the Project Management Body of Knowledge. [5]
[4]A Guide to the Project Management Body of Knowledge (PMBOK Guide) — 2000 Edition, Project Management Institute, Newtown Square, PA, chap. 6, p. 69.
Random Variables and Their Functions in Projects
Random Variables
So far, we have discussed random events (tails coming up on a coin toss) and probability spaces (a coin toss can only be heads or tails because there is nothing else in the probability space), but we have not formally talked about the numerical value of an event. If the number of heads or tails is counted, then the count per se is a random variable, CH for heads and CT for tails. [6] "Random variables" is the term we apply to numerical outcomes of events when the value cannot be known in advance of the event and where the value is a number within a range of numbers. When a random event is completed, like tossing a coin 100 times, then the random variables will have specific values obtained by counting, measuring, or observing. In the project world, task durations denoted D with values in hours, days, or weeks and cost figures denoted C with values in dollars, pesos, or euros are two among many random variables project managers will encounter.
If a variable is not a random variable, then it is a deterministic or single-point variable. A deterministic variable has no distribution of values but rather has one and only one value, and there is no uncertainty (risk) as to its measure.
As examples of random and deterministic variables, let us say that we measure cost with variable C and that C is a random variable with observed values of $8, $9, $10, $12, and $15. The range of values is therefore from $8 to $15. We do not know C with certainty, but we have an expectation that any value of C would be between $8 and $15. If C were deterministic and equal to $13.50, then $13.50 is the only value C can have. Thus, $13.50 is a risk-free measure of C.
If C were a random variable with values from $8 to $15, we would also be interested in the probability of C taking on a value of $8 or $12 or any of the other values. Thus we associate with C not only the range of values but also the probability that any particular value will occur.
Probability Functions
Random variables do not have deterministic values. In advance of a random outcome, like the uncertain duration or cost of a work package, the project team can only estimate the probable values, but the team will not know for sure what value is taken until the outcome occurs. Of course, we do not know for sure that the event will happen at all. The event itself can only be predicted probabilistically.
In the coin toss, the probability of any specific value of H or T happens to be the same: H = 1 or 0 on any specific toss, 1 if heads, else 0, and similarly for T.
p(H = T = 50 in toss of 100) = 0.5
But equal values may not be the case for all random variables in all situations.
p(D = 7 in one roll of two die) = 1/6 = 0.167
p(D = 5 in one roll of two die) = 1/9 = 0.111
where D = value of the sum of the two faces of the die on a single roll.
The probability function [7] is the mathematical relationship between a random variable's value and the probability of obtaining that value. In effect, the probability function creates a functional relationship between a probability and an event:
f(X | value) = p(X = some condition or value)
f(X | a) = p(X = a), where the "|" is the symbol used to mean "evaluated at" or "given a value of the number "a". Example: f(H | true) = 0.5 from the coin toss.
Discrete Random Variables
So far, our examples of random variables have been discrete random variables. H or T could only take on discrete values on any specific toss: 1 or 0. On any given toss, we have no way of knowing what value H or T will take, but we can estimate or calculate what the probable outcomes are, and we can say for certain, because the random variables are discrete, that they will not take on in-between values. For sure, H cannot take on a value of 0.75 on any specific toss; only values of 1 (true) or 0 (false) are allowed. Sometimes knowing what values cannot happen is as important as knowing what values will happen.
Random variables are quite useful in projects when counting things that have an atomic size. People, for instance, are discrete. There is no such thing as one-half a person. Many physical and tangible objects in projects fit this description. Sometimes actions by others are discrete random variables in projects. We may not know at the outset of a project if a regulation will be passed or a contract option exercised, but we can calculate the probability that an action will occur, yes or no.
Many times there is no limit to the number of values that random variables can take on in the allowed range. There is no limit to how close together one value can be to the next; values can be as arbitrarily close together as required. The only requirement is that for any and all values of the discrete random variable, the sum of all their probabilities of occurrences equals 1:
∑ all fi(X | ai) = 1, for i = 1 to "n"
where fi(X) is one of "n" probability functional values for the random variable, there being one functional value for each of the "n" values that X can take on in the probability space, and "ai" is the ith probable value of X.
In the coin toss experiment, "n" = 2 and "a" could have one of two values: 1 or 0. In the dice roll, "n" = 36; the values are shown in Table 2-1.
Continuous Random Variables
As the number of values of X increases in a given range of values, the spacing between them becomes smaller, so small in the limit that one cannot distinguish between one unique value and another. So also do the value's individual probabilities become arbitrarily small in order not to violate the rule about all probabilities adding up to 1. Such a random variable is called a continuous random variable because there is literally no space between one value and another; one value flows continuously to the next. Curiously, the probability of a specific value is arbitrarily near but not equal to 0. However, over a small range, say from X1 to X1 + dX, the probability of X being in this range is not necessarily small. [8]
As the number of elements in the probability function becomes arbitrarily large, the ∑ morphs smoothly to the integral ∫: ∫a-b all f(X) dX means integrate over all continuous values of X from values of alower to bupper
∫a-b all f(X) dX = 1
There are any number of continuous random variables in projects, or random variables that are so nearly continuous as to be reasonably thought of as continuous. The actual cost range of a work breakdown structure work package, discrete perhaps to the penny but for most practical applications continuous, is one example. Schedule duration range is another if measured to arbitrarily small units of time. Lifetime ranges of tools, facilities, and components are generally thought of as continuous.
Cumulative Probability Functions
It is useful in many project situations to think of the accumulating probability of an event happening. For instance, it might be useful to convey to the project sponsor that "...there is a 0.6 probability that the schedule will be 10 weeks or shorter." Since the maximum cumulative probability is 1, at some point the project manager can declare "...there is certainty, with probability 1, that the schedule will be shorter than x weeks."
We already have the function that will give us this information; we need only apply it. If we sum up the probability functions of X over a continuous range of values, ai, then we have what we want: ∑ all fi(X | ai) = 1, for i = "m" to "n" accumulates the probabilities of values between the limits of "m" and "n".
Table 2-2 provides an example of how a cumulative probability function works for a discrete random variable.
|
A |
B |
C |
|---|---|---|
|
Outcome of Random Variable Di for an Activity Duration |
Probability Density of Outcome Di |
Cumulative Probability of Outcome Di |
|
3 days |
0.1 |
0.1 |
|
5 days |
0.3 |
0.4 |
|
7 days |
0.4 |
0.8 |
|
10 days |
0.15 |
0.95 |
|
20 days |
0.05 |
1.0 |
|
|
||
|
Di is an outcome of an event described by the random variable D for task duration. |
||
|
The probability of a single-valued outcome is given in column B; the accumulating probability that the duration will be equal to or less than the outcome in column A is given in column C. |
||
Of course, for a continuous random variable, it is pretty much the same. We integrate from one limit of value to another to find the probability of the value of X hitting in the range between the limits of integration. For our purposes, integration is nothing more than summation with arbitrarily small separation between values.
[6]Italicized bold capital letters will be used for random variables.
[7]The probability function is often called the "probability density function." This name helps distinguish it from the cumulative probability function and also fits with the idea that the probability function really is a density, giving probability per value.
[8]"dX" is a notation used to mean a small, but not zero, value. Readers familiar with introductory integral calculus will recognize this convention.
Probability Distributions for Project Managers
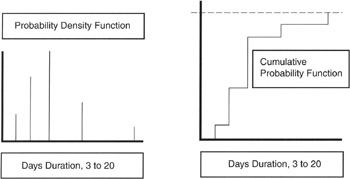
If we plot the probability (density) function (PDF) on a graph with vertical axis as probability and horizontal axis as value of X, then that plot is called a "distribution." The PDF is aptly named because the PDF shows the distribution of value according to the probability that that value will occur, as illustrated in Figure 2-3. [9] Although the exact numerical values may change from one plot to the next, the general patterns of various plots are recognizable and have well-defined attributes. To these patterns we give names: Normal distribution, BETA distribution, Triangular distribution, Uniform distribution, and many others. The attributes also have names, such as mean, variance, standard distribution, etc. These attributes are also known as statistics.
Figure 2-3: Probability Distribution.
Uniform Distribution
The discrete Uniform distribution is illustrated in Figure 2-4. The toss of the coin and the roll of the single die are discrete Uniform distributions. The principal attribute is that each value of the random variable has the same probability. In engineering, it is often useful to have a random number generator to simulate seemingly totally random events, each event being assigned a unique number. It is very much desired that the random numbers generated come from a discrete Uniform distribution so that no number, thus no event, is more likely than another.
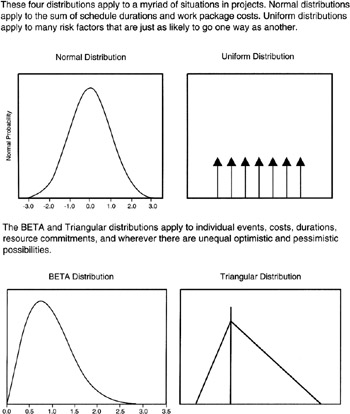
Figure 2-4: Common Distributions in Projects.
If the random variable is continuous, or the values of the discrete random variable are so close together so as to be approximately continuous, then, like all continuous distributions, the vertical axis is scaled such that the "area under the curve" equals 1. Why so? This is just a graphical way of saying that if all probabilities for all values are integrated, then the total will come to 1.
Recall: ∫a-b all f(X) dX = 1
where dX represents an increment on the horizontal axis and f(X) represents a value on the vertical axis. Vertical * horizontal = area. Thus, mathematical integration is an area calculation.
Triangular Distribution
The Triangular distribution is applied to continuous random variables. The Triangular distribution is usually shown with a skew to one side or the other. The Triangular distribution portrays the situation that not all outcomes are equally likely as was the case in the Uniform distribution. The Triangular distribution has finite tails that meet the horizontal value axis at some specific value.
There is little in nature that has a Triangular distribution. However, it is a good graphical and mathematical approximation to many events that occur in projects. Project management, like engineering, relies heavily on approximation for day-to-day practice. For instance, the approximate behavior of both cost work packages and schedule task durations can be modeled quite well with the Triangular distribution. The skew shows the imbalance in pessimism or optimism in the event.
The BETA Distribution
The BETA distribution is a distribution with two parameters, typically denoted "a" and "b" in its PDF, that influence its shape quite dramatically. Depending on the values of "a" and "b", the BETA distribution can be all the way from approximately Uniform to approximately Normal. [10] However, forms of the BETA distribution that are most useful to projects are asymmetrical curves that look something like rounded-off triangles. Indeed, it is not incorrect to think that the Triangular distribution approximates the BETA distribution. But for the rounded-off appearance of the BETA distribution, it appears in many respects the same as the Triangular distribution, each having a skew to one side or the other and each having finite tails that come down to specific values on the horizontal value axis. Events that happen in nature rarely, if ever, have distinct endpoints. Mother Nature tends to smooth things out. Nevertheless, the BETA distribution approximates many natural events quite well.
The Normal Distribution
The Normal distribution is a well-known shape, sometimes referred to as the "bell curve" for its obvious similarity to a bell. In some texts, it will be referred to as the Gaussian distribution after the 19th century mathematician Carl Friedrich Gauss. [11] The Normal distribution is very important generally in the study of probability and statistics and useful to the project manager for its rather accurate portrayal of many natural events and for its relationship to something called the "Central Limit Theorem," which we will address shortly.
Let's return to the coin toss experiment. The values of H and T are uniformly distributed: H or T can each be either value 1 or value 0 with equal probability = 0.5. But consider this: the count of the number of times T comes up heads in 100 tosses is itself a random variable. Let CT stand for this random variable. CT has a distribution, as do all random variables. CT's distribution is Normal, with the value of 50 counts of T at the center. At the tails of the Normal distribution are the counts of T that are not likely to occur if the coin is fair.
Theoretically, the Normal distribution's tails come asymptotically close to the horizontal axis but never touch it. Thus the integration of the PDF must extend to "infinite" values along the horizontal axis in order to fully define the area under the curve that equals 1. As a practical matter, project managers and engineers get along with a good deal less than infinity along the horizontal axis. For most applications, the horizontal axis that defines about 99% of the area does very nicely. In the "Six Sigma" method, as we will discuss, a good deal more of the horizontal axis is used, but still not infinity.
Other Distributions
There are many other distributions that are useful in operations, sales, engineering, etc. They are amply described in the literature, [12] and a brief listing is given in Table 2-3.
|
Distribution |
General Application |
|---|---|
|
Poisson |
|
|
Binomial |
|
|
Rayleigh |
|
|
Student's t |
|
|
Chi-square |
|
[9]The probability function is also known as the "distribution function" or "probability distribution function."
[10]If the sum of "a" and "b" is a large number, then the BETA will be more narrow and peaked than a Normal; the ratio of a/b controls the asymmetry of the BETA.
[11]Carl Friedrich Gauss (1777-1855) in 1801 published his major mathematical work, Disquisitiones Arithmeticae. Gauss was a theorist, an observer, astronomer, mathematician, and physicist.
[12]Downing, Douglas and Clark, Jeffery, Statistics the Easy Way, Barrons Educational Series, Hauppauge, NY, 1997, pp. 90–155.
Key Statistics Used in Projects
Strictly speaking, statistics are data. The data need not be a result of analysis. Statistics are any collection of data. We often hear, "What are the statistics on that event?" In other words, what are the numbers that are meaningful for understanding? Perhaps the most useful definition of statistics is that statistics is the "methods and techniques whereby collections of data are analyzed to obtain understanding and knowledge." [13] Statistical methods are by and large methods of approximation and estimation. As such, statistical methods fit very well with project management since the methods of project management are often approximate and based only on estimates.
Informational data, of course, are quite useful to project managers and to members of the project management team for estimating and forecasting, measuring progress, assessing value earned, quantifying risk, and calculating other numerical phenomena of importance to the project. Statistical methods provide some of the tools for reducing such data to meaningful information which the team uses to make decisions.
Expected Value and Average
The best-known statistic familiar to everyone is "average" (more properly, arithmetic average), which is arithmetically equal to a specific case of expected value. Expected value, E, is the most important statistic for project managers. The idea of expected value is as follows: In the face of uncertainty about a random variable that has values over a range, "expected value" [14] is the "best" single number to represent a range of estimated value of that random variable. "Best" means expected value is an unbiased maximum likelihood estimator for the population mean. [15] We will discuss unbiased maximum likelihood estimators more in subsequent paragraphs. Reducing a range of value to a single number comes into play constantly. When presenting a budget estimate to project sponsors, more often than not, only one number will be acceptable, not a range. The same is true for schedule, resource hours, and a host of other estimated variables.
Mathematically, to obtain expected value we add up all the values that a random variable can take on, weighting or multiplying each by the probability that that value will occur. Sound familiar? Except for "weighting each value by the probability," the process is identical to calculating the arithmetic average. But wait: in the case of the arithmetic average, there actually are weights on each value, but every weight is 1/n. Calculating expected value, E:
- E(X) = [(p1 * X1) + (p2 * X2) + (p3 * X3) + (p4 * X4) + ...]
- E(X) = ∑ (pi * Xi) for all values of "i"
where pi is the probability of specific value Xi occurring. If pi = 1/n, where "n" is the number of values in the summation, then E(X) is mathematically equal to the calculation of arithmetic average.
Consider this example: a work package manager estimates a task might take 2 weeks to complete with a 0.5 probability, optimistically 1.5 weeks with a 0.3 probability, but pessimistically it could take 5 weeks with a 0.2 probability. What is the expected value of the task duration?
- E(task duration D) = 0.3 * 1.5w + 0.5 * 2 + 0.2 * 5w
- E(task duration D) = 2.45w
Check yourself on the "p"s:
p1 + p2 + p3 = 0.3 + 0.5 + 0.2 = 1
There are a couple of key things of which to take note. E(X) is not a random variable. As such, E(X) will have a deterministic value. E(X) does not have a distribution. E(X) can be manipulated mathematically like any other deterministic variable; E(X) can be added, subtracted, multiplied, and divided.[16]
Transforming a space of random variables into a deterministic number is the source of power and influence of the expected value. This concept is very important to the project manager. Very often, the expected value is the number that the project manager carries to the project balance sheet as the estimate for a particular item. The range of values of the distributions that go into the expected value calculation constitutes both an opportunity (optimistic end of the range) and a threat (pessimistic end of the range) to the success of the project. The project manager carries the risk element to the risk portion of the project balance sheet.
If X is a continuous random variable, then the sum of all values of X morphs into integration as we saw before. We know that pi is the shorthand for the probability function f(X | Xi), so the expected value equation morphs to:
E(X) = ∫ X * f(X | Xi) dX, integrated over all values of "X"
Fortunately, as a practical matter, project managers do not really need to deal with integrals and integral calculus. The equations are shown for their contribution to background. Most of the integrals have approximate formulas amenable to solution with arithmetic or tables of values that can be used instead.
Mean or μ
Expected value is also called the "mean" of the distribution. [17] A common notation for mean is the Greek letter "μ,". Strictly speaking, "μ" is the notation for the population mean when all values in the population range are known. If all the values in a population are not known, or cannot be measured, then the expected value of those values that are known becomes an estimate of the true population mean, μ. As such, the expected value calculated from only a sample of the population may be somewhat in error of μ. We will discuss more about this problem later.
Variance and Standard Deviation
Variance and standard deviation are measures of the spread of values around the expected value. As a practical matter for project practitioners, the larger the spread, the less meaningful is the expected value per se.
Variance and standard deviation are related functionally:
SD = sqrt(VAR) = √VAR
where VAR (variance) is always a positive number and so, therefore, is SD (standard deviation). Commonly used notation is σ = SD, σ2 = VAR.
Variance is a measure of distance or spread of a probable outcome from the expected value of the outcome. Whether the distance is "negative" or "positive" in some arbitrary coordinate system is not important for judging the significance of the distance. Thus we first calculate distance from the expected value as follows:
Distance2 = [Xi - E(X)]2
The meaning of the distance equation is as follows: the displacement or distance of a specific value of X, say for example a value of "Xi", from the expected value is calculated as the square of the displacement of Xi from E(X). Figure 2-5 illustrates the idea. Now we must also account for the probability of X taking on the value of "Xi".
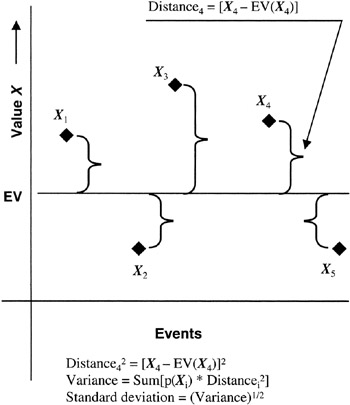
Figure 2-5: Variance and Standard Deviation.
Probabilistic distance = p(Xi) * [Xi - E(X)]2
Now, to obtain variance, we simply add up all the probabilistic distances:
VAR(X) = σ2(X) = ∑ p(X) * [Xi - E(X)]2 for all "i"
which simplifies to:
VAR(X) = σ2(X) = E(X2) - [E(X)]2
To find the standard deviation, σ, we take the square root of the variance.
Let's return to the example of task duration used in the expected value discussion to see about variance. The durations and the probability of each duration are specified. Plugging those figures into the variance equation:
σ2(task duration D) = 0.3 * (1.5 - 2.45)2 + 0.5 * (2 - 2.45)2
+ 0.2 * (5 - 2.45)2
where 2.45 weeks is the expected value of the task duration from prior calculation, σ2(task duration D) = 1.67 weeks-squared, and σ(task duration D) = 1.29 weeks. [18]
It is obvious that variance may not have physical meaning, whereas standard deviation usually does have some physical meaning. [19]
Mode
The mode of a random outcome is the most probable or most likely outcome of any single occurrence of an event. If you look at the distribution of outcome values versus their probabilities, the mode is the value at the peak of the distribution curve. Outcomes tend to cluster around the mode. Many confuse the concept of mode, the most likely outcome of any single event, with expected value, which is the best estimator of outcome considering all possible values and their probabilities. Of course, if the distribution of values is symmetrical about the mode, then the expected value and the mode will be identical.
Median
The median is the value that is half the distance between the absolute value of the most pessimistic value and the most optimistic value.
Median = 1/2 * | (optimistic value - pessimistic value)
[13]Balsley, Howard, Introduction to Statistical Method, Littlefield, Adams & Co., Totowa, NJ, 1964, pp. 3–4.
[14]Schyuler, John R., Decision Analysis in Projects, Project Management Institute, Newtown Square, PA, 1996, chap. 1, p. 11.
[15]"Best" may not be sufficiently conservative for some organizations, depending on risk attitude. Many project managers forecast with a more pessimistic estimate than the expected value.
[16]
| Caution |
Strictly speaking, arithmetic operations on the expected value depend on whether or not only linear equations of probability were involved, like summations of cost or schedule durations. For example, nonlinear effects arise in schedules due to parallel and merging paths. In such cases, arithmetic operations are only approximate, and statistical simulations are best. |
[17]You may also hear the term "moment" or "method of moments." Expected value is a "moment of X"; in fact, it is the "first moment of X." E(Xn) is called the "nth moment of X." An in-depth treatment of moments requires more calculus than is within the scope of this book.
[18]"σ" is the lower case "s" in the Greek alphabet. It is pronounced "sigma."
[19]An exception to the idea that variance has no physical meaning comes from engineering. The variance of voltage is measured in power: VAR(voltage) = watts.
The Arithmetic of Operations on Statistics and Random Variables
When it comes to arithmetic, random variables are not much different than deterministic variables. We can add, subtract, multiply, and divide random variables. For instance, we can define a random variable Z = X + Y, or W = X2. We can transform a random variable into a deterministic variable by calculating its expected value. However, many functional and logical operations on random variables depend on whether or not the variables are mutually exclusive or independent. As examples, the functional operation of expected value does not depend on independence, but the functional operation of variance does.
Similarly, there are operations on statistics that both inherit their properties from deterministic variables and acquire certain properties from the nature of randomness. For instance, the variance of a sum is the sum of variances if the random variables are independent, but the standard deviation of the sum is not the sum of the standard deviations.
Table 2-4 provides a summary of the most important operations for project managers.
|
Item |
All Arithmetic Operations |
All Functional Operations with Random Variables as Arguments |
Limiting Conditions |
|---|---|---|---|
|
Random variables |
Yes |
Yes |
|
|
Probability density functions |
Yes |
Yes |
|
|
Cumulative probability density functions |
Yes |
Yes |
If a random variable is dependent upon another, the functional expression is usually affected. |
|
Expected value, or mean, or sample average, or arithmetic average |
Yes |
Yes |
|
|
Variance |
Yes |
Yes |
If the random variables are not independent, then a covariance must be computed. |
|
Standard deviation |
Cannot add or subtract |
Yes |
To add or subtract standard deviations, first compute the sum of the variances and then take the square root. |
|
Median |
No |
No |
Median is calculated on the population or sample population of the combined random variables. |
|
Mode or most likely |
No |
No |
Most likely is taken from the population statistics of the combined random variables. |
|
Optimistic and pessimistic random variables |
Yes |
Yes |
None |
Probability Distribution Statistics
Most often we do not know every value and its probability. Thus we cannot apply the equations we have discussed to calculate statistics directly. However, if we know the probability distribution of values, or can estimate what the probability function might be, then we can apply the statistics that have been derived for those distributions. And, appropriately so for project management, we can do quite nicely using arithmetic approximations for the statistics rather than constantly referring to a table of values. Of course, electronic spreadsheets have much better approximations, if not exact values, so spreadsheets are a useful and quick tool for statistical analysis.
Three Point Estimate Approximations
Quite useful results for project statistics are obtainable by developing three-point estimates that can be used in equations to calculate expected value, variance, and standard deviation. The three points commonly used are:
- Most pessimistic value that yet has some small probability of happening.
- Most optimistic value that also has some small probability of happening.
- Most likely value for any single instance of the project. The most likely value is the mode of the distribution.
It is not uncommon that the optimistic and most likely values are much closer to each other than is the pessimistic value. Many things can go wrong that are drivers on the pessimistic estimate; usually, there are fewer things that could go right. Table 2-5 provides the equations for the calculation of approximate values of statistics for the most common distributions.
|
Statistic |
Normal [*] |
BETA[**] |
Triangular |
Uniform[***] |
|---|---|---|---|---|
|
Expected value or mean |
O + [(P - O)/2] |
(P + 4 * ML + O)/6 |
(P + ML + O)/3 |
O + [(P - O)/2] |
|
Variance, ϭ2 |
(P - O)2/36 |
(P - O)2/36 |
[(O - P)2 + (ML - O) * (ML - P)]/18 |
(P3 - O3)/ [3 * (P - O)] - (P - O)2/4 |
|
Standard deviation, ϭ |
(P - O)/6 |
(O - P)/6 |
Sqrt(VAR) |
Sqrt(VAR) |
|
Mode or most likely |
O + [(P - 0)/2] |
By observation or estimation, the peak of the curve |
By observation or estimation, the peak of the curve |
Not applicable |
|
Note: O optimistic value, P = pessimistic value, ML = most likely value. |
||||
|
[*]Formulas are approximations only to more complex functions. [**]BETA formulas apply to the curve used in PERT calculations. PERT is discussed in Chapter 7. In general, a BETA distribution has four parameters, two of which are fixed to ensure the area under the curve integrates to 1, and two, α and β, determine the shape of the curve. Normally, fixing or estimating α and β then provides the means to calculate mean and variance. However, for the BETA used in PERT, the mean and variance formulas have been worked out such that α and β become the calculated parameters. Since in most project situations the exact shape of the BETA curve does not need to be known, the calculation for α and β is not usually performed. If α and β are equal, then the BETA curve is symmetrical. If the range of values of the BETA distributed random variable is normalized to a range of 0 to 1, then for means less than 0.5 the BETA curve will be skewed to the right; the curve will be symmetrical for mean = 0.5 and skewed left if the mean is greater than 0.5. [***]In general, variance is calculated as Var(X) = E(X2) - [E(X)]2. This formula is used to derive the variance of the Triangular and Uniform distributions. The variance for the Uniform reduces to (P - O)2/12 if the optimistic value is 0; similarly, the standard deviation reduces to (P - O)/3.45. |
||||
It is useful to compare the more common distributions under the conditions of identical estimates. Figure 2-6 provides the illustration. Rules of thumb can be inferred from this illustration:
- As between the Normal, BETA, and Triangular distributions for the same estimates of optimism and pessimism (and the same mode for the BETA and Triangular), the expected value becomes more pessimistic moving from BETA to Triangular to Normal distribution.
- The variance and standard deviation of the Normal and BETA distributions are about the same when the pessimistic and optimistic values are taken at the 3σ point. However, since the BETA distribution is not symmetrical, the significance of the standard deviation as a measure of spread around the mean is not as great as in the case of the symmetrical Normal distribution.
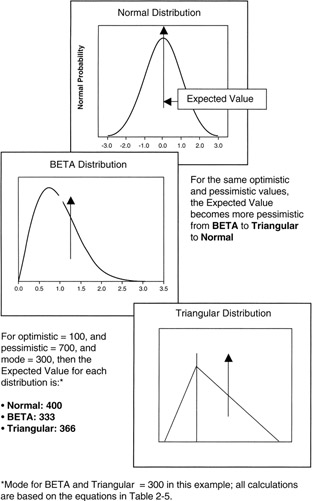
Figure 2-6: Statistical Comparison of Distributions.
In addition to the estimates given above, there are a couple of exact statistics about the Normal distribution that are handy to keep in mind:
- 68.3% of the values of a Normal distribution fall within 1σ of the mean value.
- 95.4% of the values of a Normal distribution fall within 2σ of the mean value, and this figure goes up to 99.7% for 3σ of the mean value.
- A process quality interpretation of 99.7% is that there are three errors per thousand events. If software coding were the object of the error measurement, then "three errors per thousand lines of code" probably would not be acceptable. At 6σ, the error rate is so small, 99.9998%, it is more easily spoken of in terms of "two errors per million events," about 1,000 times better than "3σ". [20]
[20]The Six Sigma literature commonly speaks of 3.4 errors per million events, not 2.0 errors per million. The difference arises from the fact that in the original program developed at Motorola, the mean of the distribution was allowed to "wander" 1.5σ from the expected mean of the distribution. This "wandering" increases the error rate from 2.0 to 3.4 errors per million events. An older shorthand way of referring to this error rate is "five nines and an eight" or perhaps "about six nines."
The Central Limit Theorem and Law of Large Numbers
Two very important concepts for the project practitioner are the Law of Large Numbers and the Central Limit Theorem because they integrate much of what we have discussed and provide very useful and easily applied heuristics for managing the quantitative aspects of projects. Let's take them one at a time.
The Law of Large Numbers and Sample Average
The Law of Large Numbers deals with estimating expected value from a large number of observations of values of events from the same population. The Law of Large Numbers will be very valuable in the process of rolling wave planning, which we will address in the chapter on scheduling.
To proceed we need to define what is meant by the "sample average":
α(x) = (1/n) * (X1 + X2 + X3 + X4 + X5 + X6 + ...)
where α(x) is the "arithmetic average of a sample of observations of random variable X," using the lower case alpha from the Greek alphabet. α(x) is a random variable with a distribution of possible values; α(x) will probably be a different value for each set of Xis that are observed.
We call α(x) a "sample average" because we cannot be sure that the Xi that we observe is the complete population; some outcomes may not be in the sample. Perhaps there are other values that we do not have the opportunity to observe. Thus, the Xi in the α(x) is but a sample of the total population. α(x) is not the expected value of X since the probability weighting for each Xi is not in the calculation; that is, α(x) is an arithmetic average, and a random variable, whereas E(X) is a probability weighted average and a deterministic nonrandom variable.
Now here is where the Law of Large Numbers comes in. It can be proved, using a couple of functions (specifically Chebyshev's Inequality and Markov's Inequality [21]), that as the number of observations in the sample gets very large, then:
α(x) ≈ E(X) = μ
This means that the sample average is approximately equal to the expected value or mean of the distribution of the population of X. Since Xi are observations from the same distribution for the population X, E(Xi) = E(X). That is, all values of X share the same population parameters or expected value and standard deviation.
Maximum Likelihood and Unbiased Estimators
Hopefully, you can see that the Law of Large Numbers simplifies matters greatly when it comes to estimating an expected value or the mean of a distribution. Without knowledge of the distribution, or knowledge of the probabilities of the individual observations, we can nevertheless approximate the expected value and estimate the mean by calculating the average of a "large" sample from the population. In fact, we call the sample average the "maximum likelihood" estimator of the mean of the population. If it turns out that the expected value of the estimator is in fact equal to the parameter being estimated, then the estimator is said to be "unbiased." The sample average is an unbiased estimator of μ since the expected value of the sample average is also μ:
E[α(x)] = E(X) = μ
The practical effect of being unbiased is that as more and more observations are added to the sample, the expected value of the estimator becomes ever increasingly identical with the parameter being estimated. If there were a bias, the expected value might "wander off" with additional observations. [22]
Working the problem the other way, if the project manager knows expected value from a calculation using distributions and three-point estimates, then the project manager can deduce that a sample might contain the Xi. In fact, using Chebyshev's Inequality we find that the probability of an Xi straying very far from the mean, μ, goes down by the square of the distance from the mean. The probability that the absolute distance of sample value Xi from the population mean is greater than some distance, y, varies by 1/y2:
p(|Xi - μ | ≥ y) ≤ σ2/y2
Sample Variance and Root Mean Square Deviation
There is one other consequence of the Law of Large Numbers that is very important in both risk management and rolling wave planning: the variance of the sample average is 1/n smaller than the variance of the population variance:
σ2[α(x)] = (1/n) * σ2(X)
σ2[α(x)] = (1/n) * [X - α(x)]2
Notice that even though the expected value of the sample average is approximately the same as the expected value of the population, the variance of the sample average is improved by 1/n, and of course the standard deviation of the sample average is improved by √(1/n). The standard deviation of the sample variance is often called the root-mean-square (RMS) deviation because of the fact that the standard deviation is the square root of the mean of the "squared distance."
In effect, the sample average is less risky than the general population represented by the random variable X, and therefore α(x) is less risky than a single outcome, Xi, of the general population.
For all practical purposes, we have just made the case for diversification of risk: a portfolio is less risky than any single element, whether it is a financial stock portfolio, a project portfolio, or a work breakdown structure (WBS) of tasks.
Central Limit Theorem
Every bit as important as the Law of Large Numbers is to sampling or diversification, the Central Limit Theorem helps to simplify matters regarding probability distributions to the point of heuristics in many cases. Here is what it is all about. Regardless of the distribution of the random variables in a sum or sample — for instance, (X1 + X2 + X3 + X4 + X5 + X6 + ...) with BETA or Triangular distributions — as long as their distributions are all the same, the distribution of the sum will be Normal with a mean "n times" the mean of the unknown population distribution!
∑ (X1 + X2 + X3 + X4 + X5 + X6 + ...) = S
S will have a Normal distribution regardless of the distribution of X:
E(X1 + X2 + X3 + X4 + X5 + X6 + ...) = E(S) = n * E(Xi) = n * μ
For n = ∑ i
"Distribution of the sum will be Normal" means that the distribution of the sample average, as an example, is Normal with mean = μ, regardless of the distribution of the Xi. We do not have to have any knowledge whatsoever about the population distribution to say that a "large" sample average of the population is Normal. What luck! Now we can add up costs or schedule durations, or a host of other things in the project, and have full confidence that their sum. or their average is Normal regardless of how the cost packages or schedule tasks are distributed.
As a practical matter, even if a few of the distributions in a sum are not all the same, as they might not be in the sum of cost packages in a WBS, the distribution of the sum is so close to Normal that it really does not matter too much that it is not exactly Normal.
Once we are working with the Normal distribution, then all the other rules of thumb and tables of numbers associated with the Normal distribution come into play. We can estimate standard deviation from the observed or simulated pessimistic and optimistic values without calculating sample variance, we can work with confidence limits and intervals conveniently, and we can relate matters to others who have a working knowledge of the "bell curve."
[21]Chebyshev's Inequality: probability that the absolute distance of sample value Xi from the population mean is greater than some distance, y, varies by 1/y2: p(Xi - μ | ≥ y) ≤ σ2/y2. Markov's Inequality applies to positive values of y, so the absolute distance is not a factor. It says that the probability of an observation being greater than y, regardless of the distance to the mean, is proportional to 1/y: p(X ≥ y) ≤ E(X) * (1/y).
[22]Unlike the sample average, the sample variance, (1/n) ∑ [Xi - α(x)]2, is not an unbiased estimator of the population variance because it can be shown that its expected value is not the variance of the population. To unbias the sample variance, it must be multiplied by the factor [n/(n-1)]. As "n" gets large, you can see that this factor approaches 1. Thus, for large "n", the bias in the sample variance vanishes and it becomes a practical estimator of the population variance.
Confidence Intervals and Limits for Projects
The whole point of studying statistics in the context of projects is to make it easier to forecast outcomes and put plans in place to affect those outcomes if they are not acceptable or reinforce outcomes if they present a good opportunity for the project. It often comes down to "confidence" rather than a specific number. Confidence in a statistical sense means "with what probability will the outcome be within a range of values?" Estimating confidence stretches the project-forecasting problem from estimating the probability of a specific value for an outcome to the problem of forecasting an outcome within certain limits of value.
Mathematically, we shift our focus from the PDF to the cumulative probability function. Summing up or integrating the probability distribution over a range of values produces the cumulative probability function. The cumulative probability equals the sum (or integral) of the probability distribution over all possible outcomes.
The S Curve
Recall that the cumulative probability accumulates from 0 to 1 regardless of the actual distribution being summed or integrated. We can easily equate the accumulating value as accumulating from 0 to 100%. For example, if we accumulate all the values in a Normal distribution between 1σ of the mean, we will find 68.3% of the total value of the cumulative total. We can say with 68.3% "confidence" that an outcome from a Normal distribution will fall in the range of 1σ of the mean; the corollary is that with 31.7% confidence, an outcome will lie outside this range, either more pessimistic or more optimistic.
Integrating the Normal curve produces an "S" curve. In general, integrating the BETA and Triangular curves will also produce a curve of roughly an "S" shape. [23] Figure 2-7 shows the "S" curve.
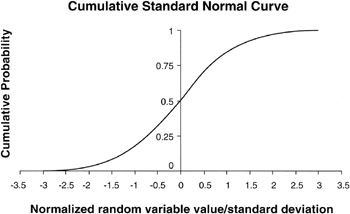
Figure 2-7: Confidence Curve for the Normal Distribution.
Confidence Tables
A common way to calculate confidence limits is with a table of cumulative values for a "standard" Normal distribution. A standard Normal distribution has a mean of 0 and a standard deviation of 1. Most statistics books or books of numerical values will have a table of standard Normal figures. It is important to work with either a "two-tailed" table or double your answers from a "one-tail" table. The "tail" refers to the curve going in both directions from the mean in the center.
A portion of a two-tailed standard Normal table is given in Table 2-6. Look in this table for the "y" value. This is the displacement from the mean along the horizontal axis. Look at y = 1, one standard deviation from the mean. You will see an entry in the cumulative column of 0.6826. This means that the "area under the curve" from 1σ is 0.6826 of all the area. The confidence of a value falling around the mean, 1σ, is 0.6826, commonly truncated to 68.3%.
|
"y" Value |
Probability |
|---|---|
|
0.1 |
0.0796 |
|
0.2 |
0.1586 |
|
0.3 |
0.2358 |
|
0.4 |
0.3108 |
|
0.5 |
0.4514 |
|
0.6 |
0.5160 |
|
0.7 |
0.5762 |
|
0.8 |
0.6318 |
|
1.0 |
0.6826 |
|
1.1 |
0.7286 |
|
1.2 |
0.7698 |
|
1.3 |
0.8064 |
|
1.4 |
0.8384 |
|
1.5 |
0.8664 |
|
1.6 |
0.8904 |
|
1.7 |
0.9108 |
|
1.8 |
0.9282 |
|
1.9 |
0.9426 |
|
2.0 |
0.9544 |
|
2.1 |
0.9643 |
|
2.2 |
0.9722 |
|
2.3 |
0.9786 |
|
2.4 |
0.9836 |
|
2.5 |
0.9876 |
|
2.6 |
0.9907 |
|
2.7 |
0.9931 |
|
2.8 |
0.9949 |
|
2.9 |
0.9963 |
|
3.0 |
0.9974 |
|
For p(-y < Xi < y) where Xi is a standard normal random variable of mean 0 and standard deviation of 1. |
|
|
For nonstandard Normal distributions, look up y = a/σ, where "a" is the value from a nonstandard distribution with mean = 0 and σ is the standard deviation of that nonstandard Normal distribution. |
|
|
If the mean of the nonstandard Normal distribution is not equal to 0, then "a" is adjusted to "a = b - μ," where "b" is the value from the nonstandard Normal distribution with mean μ: y = (b - μ)/σ. |
|
[23]For a normal curve, the slope changes such that the curvature goes from concave to convex at exactly 1σ from the mean. This curvature change will show up as an inflection on the cumulative probability curve.
Covariance and Correlation in Projects
It often arises in the course of executing projects that one or more random variables, or events, appear to bear on the same project problem. For instance, fixed costs that accumulate period by period and the overall project schedule duration are two random variables with obvious dependencies. Two statistical terms come into play when two or more variables are in the same project space: covariance and correlation.
Coveriance
Covariance is a measure of how much one random variable depends on another. Typically, we think in terms of "if X gets larger, does Y also get larger or does Y get smaller?" The covariance will be negative for the latter and positive for the former. The value of the covariance is not particularly meaningful since it will be large or small depending on whether X and Y are large or small. Covariance is defined simply as:
Cov(X,Y) = E(X * Y) - E(X) * E(Y)
If X and Y are independent, then E(X * Y) = E(X) * E(Y), and COV(X,Y) = 0.
Table 2-7 provides a project situation of covariance involving the interaction of cost and schedule duration on a WBS work package. The example requires an estimate of cost given various schedule possibilities. Once these estimates are made, then an analysis can be done of the expected value and variance of each random variable, the cost variable, and schedule duration variable. These calculations provide all that is needed to calculate the covariance.
Table 2-7: Covariance and Correlation Example
|
Table 2-7-A Cost * Duration Calculations |
||||
|---|---|---|---|---|
|
Work Package Duration, D Value |
Work Package Cost, $C |
p(D * C) of a Joint Outcome |
Joint Outcome, D * C |
E(D * C) |
|
2 months |
$10 |
0.1 |
20 |
2 |
|
$20 |
0.15 |
40 |
6 |
|
|
$60 |
0.05 |
120 |
6 |
|
|
3 months |
$10 |
0.2 |
30 |
6 |
|
$20 |
0.3 |
60 |
18 |
|
|
$60 |
0.08 |
180 |
14.4 |
|
|
4 months |
$10 |
0.02 |
40 |
0.8 |
|
$20 |
0.05 |
80 |
4 |
|
|
$60 |
0.05 |
240 |
12 |
|
|
Totals: |
1 |
69.2 |
||
|
Table 2-7-B Cost Calculations |
|||
|---|---|---|---|
|
Work Package Cost, $C |
p(C) of a Cost Outcome, Given All Schedule Possibilities |
E(C), $ |
σ2 Variance |
|
$10 |
0.32 |
$3.2 |
62.7 = 0.32(10 - 24)2 |
|
$20 |
0.5 |
$10 |
8 = 0.5(20 - 24)2 |
|
$60 |
0.18 |
$10.8 |
233.2 = 0.18(60 - 24)2 |
|
1 |
$24.00 |
σC2 = 304 σC2 = $17.44 |
|
|
Table 2-7-C Duration Calculations |
|||
|---|---|---|---|
|
Work Package Duration, D Value |
p(D) of a Schedule Outcome, Given All Cost Possibilities |
E(D), months |
σ2 Variance and Standard Deviation |
|
2 months |
0.3 |
0.6 |
0.2 = 0.3(2 - 2.82)2 |
|
3 months |
0.58 |
1.74 |
0.018 = 0.58(3 - 2.82)2 |
|
4 months |
0.12 |
0.48 |
0.17 = 0.12(4 - 2.82)2 |
|
1 |
2.82 |
σD2 = 0.39 σD = 0.62 month |
|
|
COV(D,C) = E(DC) - E(D) * E(C) |
|||
|
COV(D,C) = 69.2 - 2.82 * 24 = 1.52 |
|||
|
Meaning: Because of the positive covariance, cost and schedule move in the same way; if one goes up, so does the other. |
|||
|
r(DC) = COV(D,C)/(σD * σC) = 1.52/(0.62 * $17.44) = 0.14 |
|||
|
Meaning: Judging by a scale of -1 to +1, the "sensitivity" of cost to schedule is weak. |
|||
If the covariance of two random variables is not 0, then the variance of the sum of X and Y becomes:
VAR(X + Y) = VAR(X) + VAR(Y) + 2 * COV(X,Y)
The covariance of a sum becomes a governing equation for the project management problem of shared resources, particularly people. If the random variable X describes the availability need for a resource and Y for another resource, then the total variance of the availability need of the combined resources is given by the equation above. If resources are not substitutes for one another, then the covariance will be positive in many cases, thereby broadening the availability need (that is, increasing the variance) and lengthening the schedule accordingly. This broadening phenomenon is the underlying principle behind the lengthening of schedules when they are "resource leveled." [24]
Correlation
Covariance does not directly measure the strength of the "sensitivity" of X on Y; judging the strength is the job of correlation. Sensitivity will tell us how much the cost changes if the schedule is extended a month or compressed a month. In other words, sensitivity is always a ratio, also called a density, as in this example: $cost change/month change. But if cost and time are random variables, what does the ratio of any single outcome among all the possible outcomes forecast for the future? Correlation is a statistical estimate of the effects of sensitivity, measured on a scale of -1 to +1.
The Greek letter rho, ρ, used on populations of data, and "r", used with samples of data, stand for the correlation between two random variables: r(X,Y). The usual way of referring to "r" or "ρ" is as the "correlation coefficient." As such, their values can range from -1 to +1. "0" value means no correlation, whereas -1 means highly correlated but moving in opposite directions, and +1 means highly correlated moving in the same direction.
The correlation function is defined as the covariance normalized by the product of the standard deviations:
r(X,Y) = COV(X,Y)/(σX * σY)
We can now rewrite the variance equation:
VAR(X + Y) = VAR(X) + VAR(Y) + 2 * ρ(σX + σY)
Table 2-7 provides a project example of correlation.
[24]A Guide to the Project Management Body of Knowledge (PMBOK Guide) — 2000 Edition, Project Management Institute, Newtown Square, PA, chap. 6, p. 76.
Summary of Important Points
Table 2-8 provides the highlights of this chapter.
|
Point of Discussion |
Summary of Ideas Presented |
|---|---|
|
No facts about the future |
|
|
Probability and projects |
|
|
Random variables |
|
|
Probability distributions for projects |
|
|
|
|
Useful statistics for project managers |
|
|
Statistics of distributions |
|
|
The Law of Large Numbers and the Central Limit Theorem |
|
|
Confidence limits |
|
|
Covariance and correlation |
|
References
1. A Guide to the Project Management Body of Knowledge (PMBOK Guide) — 2000 Edition, Project Management Institute, Newtown Square, PA, chap. 6, p. 69.
2. Downing, Douglas and Clark, Jeffery, Statistics the Easy Way, Barrons Educational Series, Hauppauge, NY, 1997, pp. 90–155.
3. Balsley, Howard, Introduction to Statistical Method, Littlefield, Adams & Co., Totowa, NJ, 1964, pp. 3–4.
4. Schyuler, John R., Decision Analysis in Projects, Project Management Institute, Newtown Square, PA, 1996, chap. 1, p. 11.
5. A Guide to the Project Management Body of Knowledge (PMBOK Guide) — 2000 Edition, Project Management Institute, Newtown Square, PA, chap. 6, p. 76.
Preface
- Project Value: The Source of all Quantitative Measures
- Introduction to Probability and Statistics for Projects
- Organizing and Estimating the Work
- Making Quantitative Decisions
- Risk-Adjusted Financial Management
- Expense Accounting and Earned Value
- Quantitative Time Management
- Special Topics in Quantitative Management
- Quantitative Methods in Project Contracts
EAN: 2147483647
Pages: 97