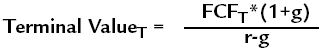Methods for Discounting Cash Flows and Residual Income

Principles

Perhaps the most common valuation technique is the free cash flow method. The starting point is based on forecasting the company's free cash flows available for shareholders or to its entire set of capital providers. These include earnings, adjusted for expenses and income that are not in cash (for example, depreciation), and adjusted for required investments and changes in working capital. The series of forecast free cash flows is then brought to current values by discounting it using the company's cost of equity or overall cost of capital.

A conceptually equivalent method, the residual income method, is based on forecasting the company's excess earnings (essentially, net income after charging for the cost of the capital employed to achieve it). Similar to the free cash flow method, the series of forecasted excess earnings is then brought to current values by discounting it using the company's cost of equity. Here, investors use the intuition that a company is creating wealth only if it provides earnings that more than compensate capital providers for the risks they take. The method, which we can trace back to its origins a century ago, is widely used in academia as well as in business circles and appears, with different flavors, under names such as Economic Value Added (EVA), Super Profits, and Abnormal Earnings.

A full valuation model would require a forecast made of every income flow and balance sheet item in perpetuity. Clearly this is impractical, so the valuation process is split into two components. The first component reflects the value of the company over the forecasting period. For that period, we derive the stream of annual residual income, or free cash flows, based on detailed forecasting of revenue and expense items, as well as the balance sheet items.

The second component is analyzed by assuming some permanent (or decaying) growth rate of the forecast item (that is, residual income or free cash flow) in the last detailed forecast year and capitalizing this item. Alternatively, an expected multiple is assumed for the main estimated parameter. For example, a P/E multiple may be applied to the forecasted net income at that period. This would be based on the anticipated prevailing multiple at that point for similar companies, taking account of the company's expected ability to grow and maintain its competitive position over the long term. Note that while it is normal to have positive growth rates for other forecast parameters such as earnings, it is rare for firms to retain an ability to obtain positive residual income for long periods of time. Therefore, investors should be very careful when determining these growth rates beyond the forecasting horizon.

Naturally, the more value beyond that detailed forecasting period, the more the forecast is subject to estimation error. However, as the raw data for this second component (typically labeled as the "Terminal Value") relies on detailed analysis of earlier periods, the longer and finer the forecasts are in these periods, the better the estimate will be for the second component and therefore for the entire valuation.

Estimating the Value Component during the Projected Period

The quality of the valuation according to the DCF method basically depends on the quality of the projections of the company's future cash flows. In startups in particular, changes in the assumptions used in the financial model with respect to the company's first years of activity which seem negligible, may have a critical effect on the company's value. For instance, if you conducted a valuation of Cisco in the year 1995, a change of 1% in its projected growth rate for the next 5 years would have resulted in a difference of hundreds of percents in the company's value. Since most of the value in the valuation of companies in their early phases of development lies beyond the projected period, small changes in each of the early years (which affect the periodic cash flows after the projected period), as well as small changes in the assumptions made about the growth rates after the projected period, could have an immense effect on the outcome. Because the terminal value is based on the forecasted period, the thorough analysis of the forecasting is very important.

When forecasting the company's cash flows, it is important to examine the logic underlying the model. Arbitrary assumptions with respect to growth rates, which are dissociated from the expected growth rates in the industry in which the company operates, may sometimes lead to scenarios in which the company's share in the target market is assumed increase to a disproportionate size.

To bring the series of free cash flows (or residual income) to current value, we need to determine the proper interest rate for discounting them. This cost is the rate of return investors require for investment in a project with similar risk characteristics. That should be the cost of equity (if we forecast the series of streams for equity holders) or the weighted average cost of capital (if we forecast the series for the entire capital base).

There are many ways of estimating the cost of equity. However, it is typically derived using a combination of methods, taking into account the stage of development of the company, the industry in which it operates, and the stage of development of the industry as a whole.

Perhaps the most commonly used method for estimating the cost of equity is the Capital Asset Pricing Model (CAPM). Under this model, the cost of equity of the company (r_e) is the sum of the risk-free interest rate (r_f) and the risk premium for the market portfolio, which is then multiplied by the company's "beta" (b), which reflects the relative sensitivity of the company stock return volatility to the market returns variability. The risk premium is the required additional return for holding equity the market stock portfolio (r_m), rather than risk-free assets such as government bonds.

r_e = r_f + (r_m r_f)b

If the company is financed by equity (E) and debt (D), with corresponding interest rates of r_e and r_d, then the Weighted Average Cost of Capital (WACC) is:

WACC = [D / (D + E)] * r_d(1 t) + [E / (D + E)] * r_e

The cost of capital of the company's debt is the rate of interest on the company's debt (r_d) after tax (the rate of which is signified by the letter t).

The cost of capital is weighted according to the market value of the company's equity and debt. In the case of private companies, the calculation is made according to the financing composition by the company. However, in most cases, the entire financing of startups is based on equity. Given their high risk profile, even debt for startups could be handled as equity in most situations for valuation purposes, as it carries similar risk characteristics (and hence required return) of equity.

• Risk-free interest rate (r_f) This is the rate of interest paid on risk-free investments such as treasury bonds. This rate of interest is composed of the projected inflation and of the return that compensates investors for the long-term use of their capital. In practice, the risk-free interest rate that is customarily used for the valuation of long-term projects is the rate of return on government bonds with maturities of 10 years.

• Equity risk premium (r_m r_f) This premium indemnifies investors for the systematic risk of equity holdings. That is, this is the risk which cannot be diversified away by holding a diversified investment portfolio. In practice, the term refers to the difference between the expected returns on the equity market portfolio and on risk-free bonds. Although this parameter is supposed to be objective, different investors assume different premiums, usually between 6% and 8%, according to the perspective which one takes on the historic return differences, and the expected ones.

The difficulty of estimating the equity risk premium has been debated at length. To illustrate the divergence of opinions, the average historic (in the last 60 years) equity risk premium in the United States has been about 6%. However, some analyses suggest that the correct measure should be based on the expected risk premium as measured at each point in time, rather than on the actual, realized risk premium. Using the former method yields a value of about 3%. Assuming a risk-free rate of 6%, this means a difference of 50% in the estimated cost of equity for the average company in the United States.

In deriving the beta for the valued company, we need to consider that the capital structure of such companies is different from that of the measured company, and we must therefore adjust beta to the company's equity without debt, since beta changes in accordance with the company's capital structure. We would therefore examine the capital structure of all comparable companies and calculate their beta without financial leverage by adjusting the leveraged beta observed in the market (b_L) to the company's capital structure:

b = b_L * E / (E + D)

Deriving beta requires the firm to be publicly traded. In the case of private companies, it is therefore customary to assume a beta of similar public companies in addition to a premium due to the illiquidity of an investment in a private company.

When a startup is being valuated, it is often difficult to find a public company which resembles it. In such cases, we would use various simplifying assumptions with respect to beta and examine the sensitivity of the results to changes in beta values.

In addition to issues of estimating the equity risk premium, the actual validity of the CAPM model has been debated, and under other models, such as the Arbitrage Pricing Theory (APT), the cost of equity also considers the exposure of the company's stock returns to additional macro-economic or companies' characteristic factors.

Another delicate issue is the time-varying discount rate of companies, in particular in their early years of development or in the early stage of development of their industry. The sensitivity of companies to market conditions may change over the years, not only because of changes in the environment, but also due to the age of the company and its size in its industry. Altering the discount rate could have a dramatic effect, in particular for companies where most of their valuation stems from the far future. Simulation tools can help here.

Estimating the Value Component after the Projected Period

Even after the cash flows projected during the period of assessment are understood, the valuator must make many assumptions about the pattern of such cash flows in subsequent periods. The value is usually calculated for the end point of the projected period, based on assumptions about a fixed future growth rate (or a formula with some other pattern of growth or decline rates).

As we mentioned above, a careful derivation of this "Terminal Value" is crucial, as it is typically responsible for a large portion of the overall value of the company. It is also important to reiterate the fact that the parameters for the "Terminal Value" are based on the detailed forecasting period. The more refined the detailed forecasting period is, the better the "Terminal Value" forecasting will become, and the better the overall valuation.

Following is a simple formula for estimating such terminal value, based on the company's projected data in the last year of the projection (FCF_T), and assuming fixed future growth:

where FCF is the free cash flow, g is the company's projected fixed future growth rate, and r is the discount rate.

In practice, this formula like other similar formulas applies a multiple to the free cash flow in the last year of the projected period. This value often constitutes a material component of the company's value, at times even 80 90% of the value of a startup, which lacks almost any positive free cash flow during the projected period. Nevertheless, often little attention is paid to the calculation of this value.

The terminal value of the company may also be calculated by another method based on the company's projected earnings multiple at T, the end point of the detailed forecasting period. This multiple may be assumed based on multiples which currently exist in the market for companies in similar phases of development as those in which the company is expected to be at the end of the projected period.

Example

CellBill Ltd. is planning to manufacture revolutionary equipment which will substantially streamline the billing methods of cellular companies. The required initial and only investment is $150 million. After a detailed analysis, the entrepreneurs prepare a projection of their revenues and expenses over the next five years. They expect the expenses (as a percentage of revenue) will decrease over time, reflecting improvements in production efficiencies. The company will be liable for income tax at the rate of 40%. In addition, the company's depreciation expenses will be the same as the investment required to maintain the company's production capacity (capital expenditures), and are described in Table 9-1. For simplicity, we are ignoring tax deductibility of depreciation. The entrepreneurs forecast that their required working capital will increase every year by 15% of the increase in sales. The entrepreneurs therefore calculate the company's free cash flows for each of the coming years. They then forecast the terminal value beyond five years, and predict that the company will continue generating a free cash flow at a growth rate of 8% per year. Note that this is a high expected growth rate, and a careful selection of the growth rate should be conducted after a thorough analysis of the growth opportunities of the firm over the long run. In the example, we also assume only expenses in the aggregate, but naturally a full analysis should be conducted one line item at a time.

The risk-free interest in the market is 6%, the risk premium for investments in stock (see the discussion on the discount rate used by VCs) is 7%, and the company's beta is 2. Therefore, the company's cost of capital (the company is financed entirely by equity) is 7%*2+6%=20%.

As can be seen in Table 9-1 below, the free cash flow in the fifth year is $50 million, and therefore the free cash flow for the first period beyond that year is assumed to be $54 million = 50 x (1 + 8%), and the terminal value is therefore 54 / (20% - 8%)=$452M. The discounted value of the terminal value is 452 * (1/(1 + 20%)⁶) = 151M. Note that we are assuming here that the beta of the company will not decline although the firm is expected to grow over time, and hence is likely to converge to its industry beta, which is typically lower than 2.

Discounting the free cash flow series and the terminal value using the annual discount rate of 20% results in a present value of $200 million. Note that the terminal value reflects more than 76% of the total discounted FCF (154/200), even though the company is profitable during most of the detailed forecasting period. After taking into account the required investment of $150 million, the value of CellBill (assuming the described activities represent all of CellBill's activities, and the firm had no other assets), is $50 million.

Table 9-1. An Example of the Valuation of a Company by the DCF Method

CellBill Ltd. Sample Valuation (figures are in $ millions)	Year 1	Year 2	Year 3	Year 4	Year 5
Revenue	100	130	145	155	180
Assumed expenses (as % of sales)	90%	85%	70%	60%	50%
Expenses	90	110	101	93	90
EBIT	10	20	44	62	90
Tax rate	40%	40%	40%	40%	40%
Operating profit	6	12	26	37	54
Depreciation	10	12	15	17	20
Capital expenditures	10	12	15	17	20
Changes in net working capital	15	5	2	2	4
Free cash flow (FCF)	-9	7	24	35	50
Discounted FCF	-8	5	14	17	20
Total Detailed Period FCF:	$49
Terminal Value (TV):
Representative FCF: Terminal Value (TV): Discounted TV:		$50*(1+8%)=$54 $54/(20%-8%)=$452 $452/(1+20%)6=$151
Total Value:
Detailed Period Value: Terminal Value: Required Investment Pre-Investment Value:		$49 $151 ($150) $50
Assumptions:
Beta Equity Risk Premium Risk Free Rate		2 7% 6%
Discount Rate:		6%+2*7%=20%
Growth beyond 5th year: Working Capital Requirements (as % of sales):		8% 15%

Valuation According to Discounted Residual Income

As mentioned above, residual income is another alternative which might offer a better solution for the valuation of early-stage companies. As discussed above, it is common to find that within the forecasted period, a company's free cash flow is negative or low because the firm is still in the investment phase and most of the value lies in the terminal value.

The Residual Income model works well in most situations and with certain adjustments can help with technology-related companies in particular, as well as with other companies that have significant components of intangible assets. It incorporates available information reported by the company and market participants, as well as the characteristics of companies in their earlier years of development. The amount of income, after a charge for the cost of capital, reflects the net value created for shareholders during the period (if the measurement is based on adjusted income available to shareholders), or the value created for all capital providers (when the measure is based on adjusted operating income).

The intuition of this method is simple a company creates value if it earns more than the cost of the capital invested in it. For the purpose of the calculation, we have to examine the earnings generated, the cost of capital, and the capital invested in the company. The capital invested every year is the equity, plus changes due to investments made in the company, minus any dividends distributed, plus capitalized expenses (namely, items deducted from the income statement and added to the balance sheet as an asset). Ostensibly, the company could have operated in another field with the same financial resources, and the company's shareholders could have invested their capital in a different investment alternative bearing the same risk but yielding an appropriate return. Therefore, the real profit generated by the company is that part of the profit that exceeds the cost of the capital.

The Adjusted Residual Income (ARI) method is a refined version of the traditional residual income method. The method, described in Fuerst and Melumad (2001a, 2001b), adds important adjustments to all of the measurements of net income and invested capital. These changes turn the general model, which was conceived primarily for companies operating in traditional industries, into a model that works particularly well for knowledge-based industries and companies.

The starting point for this calculation is adjusted net income. The adjustments are mainly related to items which were included in the financial reports (or excluded from them) in a manner inconsistent with their underlying economics. For companies that rely on intellectual property, one of the main components is the adjustment for research and development investments. Under current accounting rules, this item is typically charged as an expense in the year incurred. The ARI approach is that because R&D investments greatly affect future profitability, they should be treated for valuation purposes as assets whose value depreciates over time, based on analysis of the company and the characteristics of its industry. The valuator should therefore determine the expected life of these assets by measuring the effectiveness (in short, productivity and profitability changes) of R&D in that industry or similar industries (in many industries, R&D assets tend to have a life of three to five years). Naturally, the process impacts the income figures as well as the balance sheet.

The next step in deriving the ARI is to charge for the use of capital, based on the company's cost of equity, multiplied by the adjusted equity or the weighted cost of capital, if the measures are based on net operating income and correspondingly, the total adjusted asset base. This measure gives a series of forecasts that can be discounted to current values. The sum is then added to the current equity (or total asset) base to yield the valuation.

The result of the adjustments is that a fast-growing company, which every startup aims to be, whose R&D expenses are consequently also fast-growing, will reveal its real condition, i.e., the creation of long-term value for its shareholders. For instance, assuming a capitalization of the R&D and marketing expenses of the company Real Networks from the mid-1990s forth and depreciating them over 3 5 years, reveals that the company had already then created a residual income for its shareholders, although it reported profits only about 5 years later. However, if we use a sufficiently long projection period (such as 10 years), we will often find that a valuation using the ARI method with or without the adjustments mentioned above does not materially affect the valuation. This results from the mechanism of the model, which neutralizes the effect of the timing at which the company's business actions are recorded. For example, according to the same principle, recording a revenue earlier will increase the capital basis, since it will increase the profit which is a component of the capital for the next period, and hence indirectly the annual charge of capital in future periods.

The adjusted residual income measure can also be used for several analyses, for example, by comparing the ratios of market value to adjusted residual income or adjusted capital, as in the above example.

The terminal value derivation is made in a similar fashion to the DCF method, except for the reliance on the residual income of the last year for the projected period. Economically, over time, it is hard to find companies which earn more than the cost of their capital indefinitely. Intuitively, the more profits a company accumulates above the cost of its capital, the more companies will enter its field and reduce the profitability of the industry. On the other hand, high tech provides broad possibilities for creating niches which may be protected over time, such as Microsoft, which has been earning more than its cost of capital for years (even after capitalization of its R&D and marketing expenses). However, this is a rare case, and it is customary to assume that the growth rate of the residual income will be negative, i.e., that the adjusted residual income will be reduced to zero several years after the projected period.

Is ARI different from methods involving free cash flows? Not conceptually. Both approaches come from the same formula that states that a company's value equals the sum of its discounted expected dividends and should yield the same results. However, in practice, often there would be significant differences in valuation between the results of these models. These differences have to do with the implementation effects of the models: the information requirement for estimation, the forecasting period chosen, and the company's managerial discretion over the forecasted items.