9.9. Fast Fourier Transform
9.9. Fast Fourier Transform
The program described in this section uses Scheme's complex arithmetic to compute the discrete Fourier transform (DFT) of a sequence of values [2]. Discrete Fourier transforms are used to analyze and process sampled signal sequences in a wide variety of digital electronics applications such as pattern recognition, bandwidth compression, radar target detection, and weather surveillance.
The DFT of a sequence of N input values,
![]()
is the sequence of N output values,
![]()
each defined by the equation
![]()
It is convenient to abstract away the constant amount (for given N)
![]()
in order to obtain the more concise but equivalent equation
![]()
A straightforward computation of the N output values, each as a sum of N intermediate values, requires on the order of N2 operations. A fast Fourier transform (FFT), applicable when N is a power of 2, requires only on the order of N log2 N operations. Although usually presented as a rather complicated iterative algorithm, the fast Fourier transform is most concisely and elegantly expressed as a recursive algorithm.
The recursive algorithm, which is due to Sam Daniel [4], can be derived by manipulating the preceding summation as follows. We first split the summation into two summations and recombine them into one summation from 0 to N/2 − 1.

We then pull out the common factor WmnN.
![]()
We can reduce Wm(N/2)N to 1 when m is even and −1 when m is odd, since
![]()
This allows us to specialize the summation for the even and odd cases of m = 2k
and m = 2k + 1, 0 ≤ k ≤ N/2 − 1.

The resulting summations are DFTs of the N/2-element sequences
![]()
and
![]()
Thus, the DFT of an N-element sequence can be computed recursively by interlacing the DFTs of two N/2-element sequences. If we select a base case of two elements, we can describe a recursive fast Fourier transformation (RFFT) algorithm as follows. For N = 2,

since W02 = e0 = 1. For N > 2,

with the attendant interlacing of even and odd components.
The diagram which follows is adapted from one by Sam Daniel [4] and shows the computational structure of the RFFT algorithm. The first stage computes pairwise sums and differences of the first and second halves of the input; this stage is labeled the buttery stage. The second stage recurs on the resulting subsequences. The third stage interlaces the output of the two recursive calls to RFFT, thus yielding the properly ordered sequence {X(m)}N−1m=0.
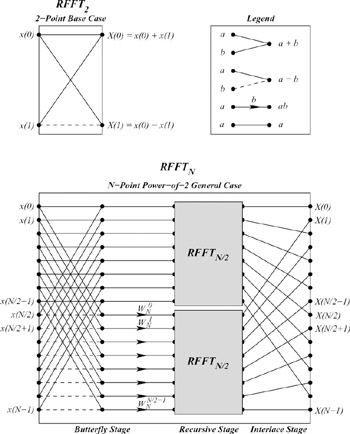
The procedure dft accepts a sequence (list) of values, x, the length of which is assumed to be a power of 2. dft precomputes a sequence of powers of WN, {WnN}N/2−1n=0, and calls rfft to initiate the recursion. rfft follows the algorithm outlined above.
(define (dft x) (define (w-powers n) (let ((pi (* (acos 0.0) 2))) (let ((delta (/ (* -2.0i pi) n))) (let f ((n n) (x 0.0)) (if (= n 0) '() (cons (exp x) (f (- n 2) (+ x delta)))))))) (define (evens w) (if (null? w) '() (cons (car w) (evens (cddr w))))) (define (interlace x y) (if (null? x) '() (cons (car x) (cons (car y) (interlace (cdr x) (cdr y)))))) (define (split ls) (let split ((fast ls) (slow ls)) (if (null? fast) (values '() slow) (call-with-values (lambda () (split (cddr fast) (cdr slow))) (lambda (front back) (values (cons (car slow) front) back)))))) (define (butterfly x w) (call-with-values (lambda () (split x)) (lambda (front back) (values (map + front back) (map * (map - front back) w))))) (define (rfft x w) (if (null? (cddr x)) (let ((x0 (car x)) (x1 (cadr x))) (list (+ x0 x1) (- x0 x1))) (call-with-values (lambda () (butterfly x w)) (lambda (front back) (let ((w (evens w))) (interlace (rfft front w) (rfft back w))))))) (rfft x (w-powers (length x))))
Exercise 9.9.1.
Alter the algorithm to employ a base case of four points. What simplifications can be made to avoid multiplying any of the base case outputs by elements of w?
Exercise 9.9.2.
Recode dft to accept a vector rather than a list as input, and have it produce a vector as output. Use lists internally if necessary, but do not simply convert the input to a list on entry and the output to a vector on exit.
Exercise 9.9.3.
Rather than recomputing the powers of w on each step for a new number of points, the code simply uses the even numbered elements of the preceding list of powers. Show that doing so yields the proper list of powers. That is, show that (evens (w-powers n)) is equal to (w-powers (/ n 2)).
Exercise 9.9.4.
The recursion step creates several intermediate lists that are immediately discarded. Recode the recursion step to avoid any unnecessary allocation.
Exercise 9.9.5.
Each element of a sequence of input values may be regenerated from the discrete Fourier transform of the sequence via the equation
![]()
Noting the similarity between this equation and the original equation defining X(m), create a modified version of dft, inverse-dft, that performs the inverse transformation. Verify that (inverse-dft (dft seq)) returns seq for several input sequences seq.
EAN: 2147483647
Pages: 98