Chapter 27. Terrain Generation with Terragen

Placing Objects in the Scene

Knowing where to place something in the scene at scene creation time is a question of knowing the height of the ground at a particular (x, z) location. This is problematic because most ground positions will have been extrapolated by Java 3D from the corner points of quads. Picking is useless in this case since we want to position objects before the complete scene is made live.

If a quad is coplanar (i.e., positioned in a single plane), then calculating interior points is straightforward. Unfortunately, most quads are not coplanar. Furthermore, because the underlying graphics hardware works with triangles, the geometry in a Shape3D will have been triangulated, and the shape of those triangles is hard to predict when their vertices are highly noncoplanar.

Java 3D uses a subset of the FIST triangulation algorithm (see http://www.cosy.sbg.ac.at/~held/projects/triang/triang.html for a nontechnical discussion of the algorithm). Each polygon is projected onto a plane, and the 2D projected points are considered using a range of heuristics. One aim is to avoid long, skinny triangles by maximizing the angles within the triangles. The presence of heuristics means that it's sometimes difficult to know how a polygon will be divided.

The example is Figure 26-11, which shows a single quad with two equally likely triangulations. A division along PR will give point pt a height of 0, but if the SQ line is used then the same point will have a height of 5 units.

Figure 26-11. A triangulation problem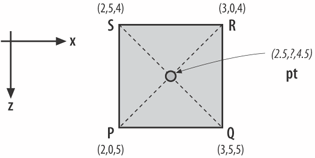

One way of dealing with this issue is to move away from quadrilaterals and use triangles as the tiling units for the terrain. An equation for the surface delineated by a triangle's three vertices (the plane equation) is easily obtained. Consider the points P, Q, and R in the triangle of Figure 26-12.

Figure 26-12. A triangle with vectors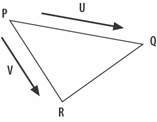

The plane equation is defined as:

Ax + By + Cz = D

where A, B, C, and D are constants.

The normal vector N is calculated with the cross product of the vectors U and V:

N = UxV

U and V are obtained by subtracting P from Q and R, respectively.

When is N is normalized (made to have unit length), then A, B, and C are its coefficients.

The distance from the origin to the point on the plane nearest to the origin is equivalent to the plane equation's D constant. D can be calculated as the dot product of the normal and any point on the triangle (e.g., the point P):

D = N . P

Once we have the plane equation coefficients, the height of any point lying on the triangle is:

y = (D - Ax - Cz )/B

where (x, z) is the known XZ position of the point.

Here is the Java 3D code for doing this:

     private void vecsToHeight(Vector3d u, Vector3d v, Vector3d pt)     {       Vector3d normal = new Vector3d(  );       normal.cross(u, v);       normal.normalize(  );       double dist = normal.dot(pt);           System.out.println("A: "+ df.format(normal.x) + ", B: " +                        df.format(normal.y) + ", C: " + df.format(normal.z) +                        ", D: " + df.format(dist) );    // Ax + By + Cz = D           double height = (dist - (normal.x * pt.x) - (normal.z * pt.z)) / normal.y;       System.out.println("Height for pt: " + df.format(height) );     } 

A drawback with working with triangles is the distortion apparent in textures laid over the triangles.