9.3 Belief Revision
|
9.3 Belief Revision
The most common approach to studying belief change in the literature has been the axiomatic approach. This has typically involved starting with a collection of postulates, arguing that they are reasonable, and proving some consequences of these postulates. Perhaps the most-studied postulates are the AGM postulates, named after the researchers who introduced them: Alchourr n, G rdenfors, and Makinson. These axioms are intended to characterize a particular type of belief change, called belief revision.
As I have suggested, in this approach, the agent's beliefs are represented by a set of formulas and what the agent observes is represented by a formula. More precisely, the AGM approach assumes that an agent's epistemic state is represented by a belief set, that is, a set K of formulas in a logical language ![]() , describing the subject matter about which the agent holds beliefs. For simplicity here, I assume that
, describing the subject matter about which the agent holds beliefs. For simplicity here, I assume that ![]() is propositional (which is consistent with most of the discussions of the postulates). In the background, there are also assumed to be some axioms AX
is propositional (which is consistent with most of the discussions of the postulates). In the background, there are also assumed to be some axioms AX![]() characterizing the situation. For example, for the circuit-diagnosis example of Figure 9.1,
characterizing the situation. For example, for the circuit-diagnosis example of Figure 9.1, ![]() could be
could be ![]() Prop(Φdiag). There would then be an axiom in AX
Prop(Φdiag). There would then be an axiom in AX![]() saying that if A1 is not faulty, then l5 is 1 iff both l1 and l2 are:
saying that if A1 is not faulty, then l5 is 1 iff both l1 and l2 are:
![]()
Similar axioms would be used to characterize all the other components.
Let ⊢![]() denote the consequence relation that characterizes provability from AX
denote the consequence relation that characterizes provability from AX![]() ; Σ ⊢
; Σ ⊢![]() φ holds iff φ is provable from Σ and the axioms in AX
φ holds iff φ is provable from Σ and the axioms in AX![]() , using propositional reasoning (Prop and MP). Cl(Σ) denotes the logical closure of the set Σ under AX
, using propositional reasoning (Prop and MP). Cl(Σ) denotes the logical closure of the set Σ under AX![]() ; that is, C1(Σ) = {φ : Σ ⊢
; that is, C1(Σ) = {φ : Σ ⊢![]() φ}. I assume, in keeping with most of the literature on belief change, that belief sets are closed under logical consequence, so that if K is a belief set, then Cl(K) = K. This assumption can be viewed as saying that agents are being treated as perfect reasoners who can compute all logical consequences of their beliefs. But even if agents are perfect reasoners, there may be good reason to separate the core of an agent's beliefs from those beliefs that are derived from the core. Consider the second example discussed at the beginning of the chapter, where the agent initially believes φ1 and thus also believes φ1 ∨ p. If he later learns that φ1 is false, it may be useful to somehow encode that the only reason he originally believed φ1 ∨ p is because of his belief in φ1. This information may certainly affect how his beliefs change. Although I do not pursue this issue further here, it is currently an active area of research.
φ}. I assume, in keeping with most of the literature on belief change, that belief sets are closed under logical consequence, so that if K is a belief set, then Cl(K) = K. This assumption can be viewed as saying that agents are being treated as perfect reasoners who can compute all logical consequences of their beliefs. But even if agents are perfect reasoners, there may be good reason to separate the core of an agent's beliefs from those beliefs that are derived from the core. Consider the second example discussed at the beginning of the chapter, where the agent initially believes φ1 and thus also believes φ1 ∨ p. If he later learns that φ1 is false, it may be useful to somehow encode that the only reason he originally believed φ1 ∨ p is because of his belief in φ1. This information may certainly affect how his beliefs change. Although I do not pursue this issue further here, it is currently an active area of research.
What the agent learns is assumed to be characterized by some formula φ, also in ![]() ; K ◦ φ describes the belief set of an agent who starts with belief set K and learns φ. Two subtle but important assumptions are implicit in this notation:
; K ◦ φ describes the belief set of an agent who starts with belief set K and learns φ. Two subtle but important assumptions are implicit in this notation:
-
The functional form of ◦ suggests that all that matters regarding how an agent revises her beliefs is the belief set and what is learned. In any two situations where the agent has the same beliefs, she will revise her beliefs in the same way.
-
The notation also suggests that the second argument of ◦ can be an arbitrary formula in
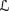 and the first can be an arbitrary belief set.
and the first can be an arbitrary belief set.
These are nontrivial assumptions. With regard to the first one, it is quite possible for two different plausibility measures to result in the same belief sets and yet behave differently under conditioning, leading to different belief sets after revision. With regard to the second one, at a minimum, it is not clear what it would mean to observe false. (It is perfectly reasonable to observe something inconsistent with one's current beliefs, but that is quite different from observing false, which is a contradictory formula.) Similarly, it is not clear how reasonable it is to consider an agent whose belief set is Cl(false), the trivial belief set consisting of all formulas. But even putting this issue aside, it may not be desirable to allow every consistent formula to be observed in every circumstance. For example, in the circuit-diagnosis problem, the agent does not observe the behavior of a component directly; she can only infer it by setting the values of some lines and observing the values of others. While some observations are essentially equivalent to observing that a particular component is faulty (e.g., if setting l1 to 1 and l2 to 1 results in l5 being 0 in the circuit of Figure 9.1, then A1 must be faulty), no observations can definitively rule out a component being faulty (the faulty behavior may display itself only sporadically).
Indeed, in general, what is observable may depend on the belief set itself. Consider a situation where an agent can reliably observe colors. After observing that a coat is blue (and thus, having this fact in her belief set), it may not be possible for her to observe that the same coat is red.
The impact of these assumptions will be apparent shortly. For now, I simply state the eight postulates used by Alchourr n, G rdenfors, and Makinson to characterize belief revision.
-
R1. K ◦ φ is a belief set.
-
R2. φ ∈ K ◦ φ.
-
R3. K ◦ φ ⊆ Cl(K ∪{φ}).
-
R4. If φ ∉ K, then Cl(K ∪{φ}) ⊆ K ◦ φ.
-
R5. K ◦ φ = Cl(false) iff ⊨
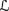 φ.
φ. -
R6. If ⊨
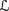 φ ⇔ ψ, then K ◦ φ = K ◦ ψ.
φ ⇔ ψ, then K ◦ φ = K ◦ ψ. -
R7. K ◦ (φ ∧ ψ) ⊆ Cl(K ◦ φ ∪{ψ}).
-
R8. If ψ ∉ K ◦ φ, then Cl(K ◦ φ ∪{ψ}) ⊆ K ◦ (φ ∧ ψ).
Where do these postulates come from and why are they reasonable? It is hard to do them justice in just a few paragraphs, but the following comments may help:
-
R1 says that ◦ maps a belief set and a formula to a belief set. As I said earlier, it implicitly assumes that the first argument of ◦ can be an arbitrary belief set and the second argument can be an arbitrary formula.
-
R2 says that the belief set that results after revising by φ includes φ. Now it is certainly not true in general that when an agent observes φ she necessarily believes φ. After all, if φ represents a somewhat surprising observation, then she may think that her observation was unreliable. This certainly happens in science; experiments are often repeated to confirm the results. This suggests that perhaps these postulates are appropriate only when revising by formulas that have been accepted in some sense, that is, formulas that the agent surely wants to include in her belief set. Under this interpretation, R2 should certainly hold.
-
R3 and R4 together say that if φ is consistent with the agent's current beliefs, then the revision should not remove any of the old beliefs or add any new beliefs except these implied by the combination of the old beliefs with the new belief. This property certainly holds for the simple notion of conditioning knowledge by intersecting the old set of possible worlds with the set of worlds characterizing the formula observed, along the lines discussed in Section 3.1. It also is easily seen to hold if belief is interpreted as "holds with probability 1" and revision proceeds by conditioning. The formulas that hold with probability 1 after conditioning on φ are precisely those that follow from φ together with the formulas that held before. Should this hold for all notions of belief? As the later discussion shows, not necessarily. Note that R3 and R4 are vacuous if φ ∈ K (in the case of R3, this is because, in that case, Cl(K ∪{φ}) consists of all formulas). Moreover, note that in the presence of R1 and R2, R4 can be simplified to just K ⊆ K ◦ φ, since R2 already guarantees that φ ∈ K ◦ φ, and R1 guarantees that K ◦ φ is a belief set, hence a closed set of beliefs.
-
Postulate R5 discusses situations that I believe, in fact, should not even be considered. As I hinted at earlier, I am not sure that it is even appropriate to consider the trivial belief set Cl(false), nor is it appropriate to revise by false (or any formula logically equivalent to it; i.e., a formula φ such that ⊨
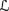 φ). If the trivial belief and revising by contradictory formulas were disallowed, then R5 would really be saying nothing more than R1. If revising by contradictory formulas is allowed, then taking K ◦ φ = Cl(false) does seem reasonable if φ is contradictory, but it is less clear what Cl(false) ◦ φ should be if φ is not contradictory. R5 requires that it be a consistent belief set, but why should this be so? It seems just as reasonable that, if an agent ever has incoherent beliefs, then she should continue to have them no matter what she observes.
φ). If the trivial belief and revising by contradictory formulas were disallowed, then R5 would really be saying nothing more than R1. If revising by contradictory formulas is allowed, then taking K ◦ φ = Cl(false) does seem reasonable if φ is contradictory, but it is less clear what Cl(false) ◦ φ should be if φ is not contradictory. R5 requires that it be a consistent belief set, but why should this be so? It seems just as reasonable that, if an agent ever has incoherent beliefs, then she should continue to have them no matter what she observes. -
R6 states that the syntactic form of the new belief does not affect the revision process; it is much in the spirit of the rule LLE in system P from Section 8.3. Although this property holds for all the notions of belief change I consider here, it is worth stressing that this postulate is surely not descriptively accurate. People do react differently to equivalent formulas (especially since it is hard for them to tell that they are equivalent; this is a problem that is, in general, co-NP complete).
-
Postulates R7 and R8 can be viewed as analogues of R3 and R4 for iterated revision. Note that, by R3 and R4, if ψ is consistent with K ◦ φ (i.e., if ψ ∉ K ◦ φ), then (K ◦ φ) ◦ ψ = Cl(K ◦ φ ∪{ψ}). Thus, R7 and R8 are saying that if ψ is consistent with K ◦ φ, then K ◦ (φ ∧ ψ) = (K ◦ φ) ◦ ψ. As we have seen, this is a property satisfied by probabilistic conditioning: if μ(U1 ∩ U2) ≠ 0, then (μ| U1)|U2 = (μ|U2)|U1 = μ|(U1 ∩ U2).
As the following example shows, conditional probability measures provide a model for the AGM postulates:
Example 9.3.1
Fix a finite set Φ of primitive propositions. Let ⊨![]() be a consequence relation for the language
be a consequence relation for the language ![]() Prop(Φ). Since Φ is finite, ⊨
Prop(Φ). Since Φ is finite, ⊨![]() can be characterized by a single formula σ ∈
can be characterized by a single formula σ ∈ ![]() Prop(Φ); that is, ⊨
Prop(Φ); that is, ⊨![]() iff σ ⇒ φ is a propositional tautology (Exercise 9.7(a)). Let M = (W, 2W, 2W − ∅, μ, π) be a simple conditional probability structure, where π is such that (a) (M, w) ⊨ σ for all w ∈ W and (b) if σ ∧ ψ is satisfiable, then there is some world w ∈ W such that (M, w) ⊨ ψ. Let K consist of all the formulas to which the agent assigns unconditional probability 1; that is, K ={ψ : μ([[ψ]]M) = 1}. If [[φ]]M ≠ ∅, define K ◦ φ ={ψ : μ([[ψ]]M | [[φ]]M) = 1}. That is, the belief set obtained after revising by φ consists of just those formulas whose conditional probability is 1; if [[φ]]M = ∅, define K ◦ φ = Cl(false). It can be checked that this definition of revision satisfies R1–8 (Exercise 9.7(b)). Moreover, disregarding the case where K = Cl(false) (a case I would argue should never arise, since an agent should also have consistent beliefs), then every belief revision operator can in a precise sense be captured this way (Exercise 9.7(c)).
iff σ ⇒ φ is a propositional tautology (Exercise 9.7(a)). Let M = (W, 2W, 2W − ∅, μ, π) be a simple conditional probability structure, where π is such that (a) (M, w) ⊨ σ for all w ∈ W and (b) if σ ∧ ψ is satisfiable, then there is some world w ∈ W such that (M, w) ⊨ ψ. Let K consist of all the formulas to which the agent assigns unconditional probability 1; that is, K ={ψ : μ([[ψ]]M) = 1}. If [[φ]]M ≠ ∅, define K ◦ φ ={ψ : μ([[ψ]]M | [[φ]]M) = 1}. That is, the belief set obtained after revising by φ consists of just those formulas whose conditional probability is 1; if [[φ]]M = ∅, define K ◦ φ = Cl(false). It can be checked that this definition of revision satisfies R1–8 (Exercise 9.7(b)). Moreover, disregarding the case where K = Cl(false) (a case I would argue should never arise, since an agent should also have consistent beliefs), then every belief revision operator can in a precise sense be captured this way (Exercise 9.7(c)).
The fact that the AGM postulates can be captured by using conditional probability, treating revision as conditioning, lends support to the general view of revision as conditioning. However, conditional probability is just one of the methods considered in Section 8.3 for giving semantics to defaults as conditional beliefs. Can all the other approaches considered in that section also serve as models for the AGM postulates? It turns out that ranking functions and possibility measures can, but arbitrary preferential orders cannot. My goal now is to understand what properties of conditional probability make it an appropriate model for the AGM postulates. As a first step, I relate AGM revision to BCSs. More precisely, the plan is to find some additional conditions (REV1–3) on BCSs that ensure that belief change in a BCS satisfies R1–8. Doing this will help bring out the assumptions implicit in the AGM approach.
The first assumption is that, although the agent's beliefs may change, the propositions about which the agent has beliefs do not change during the revision process. The original motivation for belief revision came from the study of scientists' beliefs about laws of nature. These laws were taken to be unvarying, although experimental evidence might cause scientists to change their beliefs about the laws.
This assumption underlies R3 and R4. If φ is consistent with K, then according to R3 and R4, observing φ should result in the agent adding φ to her stock of beliefs and then closing off under implication. In particular, this means that all her old beliefs are retained. But if the world can change, then there is no reason for the agent to retain her old beliefs. Consider the systems 퓙1 and 퓙2 used to model the diagnosis problem. In these systems, the values on the line could change at each step. If l1 = 1 before observing l2 = 1, then why should l1 = 1 after the observation, even if it is consistent with the observation that l2 = 1? Perhaps if l1 is not set to 1, its value goes to 0.
In any case, it is easy to capture the assumption that the propositions observed do not change their truth value. That is the role of REV1.
REV1. π (r, m) (p) = π (r, 0)(p) for all p ∊ Φe and points (r, m).
Note that REV1 does not say that all propositions are time invariant, nor that the environment state does not change over time. It simply says that the propositions in Φe do not change their truth value over time. Since the formulas being observed are, by assumption, in ![]() e, and so are Boolean combinations of the primitive propositions in Φe, their truth values also do not change over time. In the model in Example 9.3.1, there is no need to state REV1 explicitly, since there is only one time step. Considering only one time step simplifies things, but the simplification sometimes disguises the subtleties.
e, and so are Boolean combinations of the primitive propositions in Φe, their truth values also do not change over time. In the model in Example 9.3.1, there is no need to state REV1 explicitly, since there is only one time step. Considering only one time step simplifies things, but the simplification sometimes disguises the subtleties.
In the BCSs 퓙1 and 퓙2, propositions of the form faulty(c) do not change their truth value over time, by assumption; however, propositions of the form hi(l) do. There is a slight modification of these systems that does satisfy REV1. The idea is to take ![]() e to consist only of Boolean combinations of formulas of the form faulty(c) and then convert the agent's observations to formulas in
e to consist only of Boolean combinations of formulas of the form faulty(c) and then convert the agent's observations to formulas in ![]() e. Note that to every observation o made by the agent regarding the value of the lines, there corresponds a formula in
e. Note that to every observation o made by the agent regarding the value of the lines, there corresponds a formula in ![]() e that characterizes all the fault sets that are consistent with o. For example, the observation hi(l1) ∧ hi(l2) ∧ hi(l4) corresponds to the conjunction of the formulas characterizing all fault sets that include X1 (which is equivalent to the formula faulty(X1)). For every observation φ about the value of lines, let φ† ∈
e that characterizes all the fault sets that are consistent with o. For example, the observation hi(l1) ∧ hi(l2) ∧ hi(l4) corresponds to the conjunction of the formulas characterizing all fault sets that include X1 (which is equivalent to the formula faulty(X1)). For every observation φ about the value of lines, let φ† ∈ ![]() e be the corresponding observation regarding fault sets. Given a run r ∈ 퓙i, i = 1, 2, let r† be the run where each observation φ is replaced by φ†. Let 퓙†i be the BCS consisting of all the runs r† corresponding to the runs in 퓙i. The plausibility assignments in 퓙i† and 퓙i correspond in the obvious way. That means that the agent has the same beliefs about formulas in
e be the corresponding observation regarding fault sets. Given a run r ∈ 퓙i, i = 1, 2, let r† be the run where each observation φ is replaced by φ†. Let 퓙†i be the BCS consisting of all the runs r† corresponding to the runs in 퓙i. The plausibility assignments in 퓙i† and 퓙i correspond in the obvious way. That means that the agent has the same beliefs about formulas in ![]() e at corresponding points in the two systems. More precisely, if φ ∈
e at corresponding points in the two systems. More precisely, if φ ∈ ![]() e, then (퓙i†, r†, m) ⊨ φ if and only if (퓙i, r, m) ⊨ φ for all points (r, m) in 퓙i. Hence, (퓙i†, r†, m) ⊨ Bφ if and only if (퓙i, r, m) ⊨ Bφ. By construction, 퓙†i, i = 1, 2, are BCSs that satisfy REV1.
e, then (퓙i†, r†, m) ⊨ φ if and only if (퓙i, r, m) ⊨ φ for all points (r, m) in 퓙i. Hence, (퓙i†, r†, m) ⊨ Bφ if and only if (퓙i, r, m) ⊨ Bφ. By construction, 퓙†i, i = 1, 2, are BCSs that satisfy REV1.
Belief change in 퓙†1 can be shown to satisfy all of R1–8 in a precise sense (see Theorem 9.3.5 and Exercise 9.11); however, 퓙†2 does not satisfy either R4 or R8, as the following example shows:
Example 9.3.2
Consider Example 9.1.4 again. Initially (before making any observations) that agent believes that no components are faulty. Recall that the agent sets l1 = l and l2 = l3 = 0, then observes that l8 is 1. That is, the agent observes φ = hi(l1) ∧ hi(l2) ∧ hi(l3). It is easy to see that φ† is faulty(X1) ∨ faulty(A1) ∨ faulty(A2) ∨ faulty(O1). Since the agent prefers minimal explanations, Bel(퓙†2, 〈φ†〉) includes the belief that exactly one of X1, A1, A2, or O1 is faulty. Let K = Bel(퓙†2, 〈〉). Think of Bel(퓙†2, 〈φ†〉) as K ◦ φ†. Suppose that the agent then observes l7 is 0, that is, the agent observes ψ = hi(l7)). Now ψ† says that the fault set contains X1 or contains both X2 and one of A1, A2, or O1. Notice that ψ† implies φ†. Thus, Bel(퓙†2, 〈φ†, ψ†〉) = Bel(퓙†2, 〈φ† ∧ ψ†〉) = Bel(퓙†2, 〈ψ†〉). That means that (K ◦ φ†) ◦ ψ† = ![]() ◦ (φ† ∧ ψ†), and this belief set consists of the belief that the fault set is exactly one of X1, {X2, A1}, {X2, A2}, and {X2, O1}, and all of the consequences of this belief. On the other hand, it is a consequence of K ◦ φ†∪{ψ†} that X1 is the only fault. Thus,
◦ (φ† ∧ ψ†), and this belief set consists of the belief that the fault set is exactly one of X1, {X2, A1}, {X2, A2}, and {X2, O1}, and all of the consequences of this belief. On the other hand, it is a consequence of K ◦ φ†∪{ψ†} that X1 is the only fault. Thus,
![]()
showing that neither R4 nor R8 holds in 퓙†2
Why do R4 and R8 hold in 퓙†1 and not in 퓙†2? It turns out that the key reason is that the plausibility measure in 퓙†1 is totally ordered; in 퓙†2 it is only partially ordered. In fact, I show shortly that R4 and R8 are just Rational Monotonicity in disguise. (Recall that Rational Monotonicity is axiom C5 in Section 8.6, the axiom that essentially captures the fact that the plausibility measure is totally ordered.) REV2 strengthens BCS2 to ensure that Rational Monotonicity holds for →.
-
REV2. The conditional plausibility measure Pla on runs that is guaranteed to exist by BCS2 satisfies Pl6 (or, equivalently, Pl7 and Pl8; see Section 8.6); more precisely, Pl( | U) satisfies Pl6 for all sets U of runs in
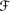 ′.
′.
Another condition on BCSs required to make belief change satisfy R1–8 makes precise the intuition that observing φ does not give any information beyond φ. As Example 3.1.2 and the discussion in Section 6.8 show, without this assumption, conditioning is not appropriate. To see the need for this assumption in the context of belief revision, consider the following example:
Example 9.3.3
Suppose that 퓙 is a BCS such that Bel(퓙, 〈〉) = C1(p). Moreover, in 퓙, the agent observes q at time 0 only if p is false and both p′ and q are true. It is easy to construct a BCS satisfying REV1 and REV2 that also satisfies this requirement (Exercise 9.8). Thus, after observing q, the agent believes p ∧ p′ ∧ q. It follows that neither R3 nor R4 hold in 퓙. Indeed, taking K = Cl(p), the fact that p′ ∈ K ◦ q means that K ◦ q ⊈ Cl(K ∪{q}), violating R3, and the fact that p ∈ K ◦ q means that K ⊈ K ◦ q (for otherwise K ◦ q would be inconsistent, and all belief sets in a BCS are consistent), violating R4. With a little more effort, it is possible to construct a BCS that satisfies REV1 and REV2 and violates R7 and R8 (Exercise 9.8)
The assumption that observations do not give additional information is captured by REV3 in much the same way as was done in the probabilistic case in Section 6.8.
-
REV3. If sa φ is a local state in 퓙 and ∈
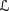 Prop(Φe), then
Prop(Φe), then 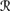 [sa] ∩
[sa] ∩ 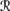 [φ] ∈
[φ] ∈  ′ and P1a(
′ and P1a( [ψ]|
[ψ]|  [sa φ] = P1a(
[sa φ] = P1a( [ψ] |
[ψ] |  [sa] ∩
[sa] ∩  [φ]).
[φ]).
(The requirement that ![]() [sa] ∩
[sa] ∩ ![]() [φ] ∈
[φ] ∈ ![]() ′ in fact follows from BCS1–3; see Exercise 9.9.) The need for REV3 is obscured if no distinction is made between φ being true and the agent observing φ. This distinction is quite explicit in the BCS framework. Note that REV3 does not require that Pla( |
′ in fact follows from BCS1–3; see Exercise 9.9.) The need for REV3 is obscured if no distinction is made between φ being true and the agent observing φ. This distinction is quite explicit in the BCS framework. Note that REV3 does not require that Pla( | ![]() [sa φ]) = Pla( |
[sa φ]) = Pla( | ![]() [sa] ∩
[sa] ∩ ![]() [φ]). It makes the somewhat weaker requirement that Pla(
[φ]). It makes the somewhat weaker requirement that Pla(![]() ′ |
′ | ![]() [sa φ]) = Pla(
[sa φ]) = Pla(![]() ′ |
′ | ![]() [sa] ∩
[sa] ∩ ![]() [φ]) only if
[φ]) only if ![]() ′ is a set of runs of the form
′ is a set of runs of the form ![]() [ψ] for some formula ψ ∈
[ψ] for some formula ψ ∈ ![]() Prop(Φe).
Prop(Φe).
It is not hard to see that REV3 fails in the BCS 퓙 constructed in Example 9.3.3. For suppose that Pla is the prior plausibility in 퓙. By assumption, in 퓙, after observing p1, the agent believes p2 and q, but after observing p1 ∧ p2, the agent believes q. Thus,
![]()
and
![]()
If REV3 held, then (9.1) and (9.2) would imply
![]()
and
![]()
From (9.3), it follows that Pla[![]() [p2] |
[p2] | ![]() [p1]) > Pla[
[p1]) > Pla[![]() [p2 ∧ q] |
[p2 ∧ q] | ![]() [p1]) > ⊥, so by CPl5 (which holds in 퓙 by BCS2) applied to (9.4), it follows that
[p1]) > ⊥, so by CPl5 (which holds in 퓙 by BCS2) applied to (9.4), it follows that
![]()
Since ![]() [ (p2 ∧ q)]
[ (p2 ∧ q)] ![]() [ q ∧ p2], it follows from CPl3 and (9.3) that
[ q ∧ p2], it follows from CPl3 and (9.3) that
![]()
contradicting (9.5). Thus, REV3 does not hold in 퓙.
Among other things, REV3 says that the syntactic form of the observation does not matter. That is, suppose that φ and φ′ are equivalent formulas, and the agent observes φ. It is possible that the observation is encoded as φ′. Should this matter? A priori, it could. REV3 says that it does not, as the following lemma shows:
Lemma 9.3.4
If φ and φ′ are equivalent formulas (i.e., ⊨![]() φ ⇔ φ′), and sa φ and sa φ′ are both states in 퓙, then Pla[
φ ⇔ φ′), and sa φ and sa φ′ are both states in 퓙, then Pla[![]() [ψ] |
[ψ] | ![]() [sa φ]) = Pla[
[sa φ]) = Pla[![]() [ψ] |
[ψ] | ![]() [sa φ′]).
[sa φ′]).
Proof See Exercise 9.10.
Let ![]()
![]()
![]() consist of all reliable BCSs satisfying REV1–3. It is easy to see that 퓙†1 ε
consist of all reliable BCSs satisfying REV1–3. It is easy to see that 퓙†1 ε![]()
![]()
![]() (Exercise 9.11). The next result shows that, in a precise sense, every BCS in
(Exercise 9.11). The next result shows that, in a precise sense, every BCS in ![]()
![]()
![]() satisfies R1–8.
satisfies R1–8.
Theorem 9.3.5
Suppose that 퓙 ∈ ![]()
![]()
![]() and sa is a local state of the agent at some point in 퓙. Then there is a belief revision operator ◦sa satisfying R1–8 such that for all φ ∈
and sa is a local state of the agent at some point in 퓙. Then there is a belief revision operator ◦sa satisfying R1–8 such that for all φ ∈ ![]() e such that the observation φ can be made in sa (i.e., for all φ such that sa φ is a local state at some point in 퓙) Bel(퓙, sa) οsa φ = Bel(퓙, sa φ).
e such that the observation φ can be made in sa (i.e., for all φ such that sa φ is a local state at some point in 퓙) Bel(퓙, sa) οsa φ = Bel(퓙, sa φ).
Proof Fix sa. If K = Bel(퓙, sa) and sa φ is a local state in 퓙, then define K ◦s, a φ = Bel(I, sa φ). (This is clearly the only definition that will satisfy the theorem.) Recall for future reference that this means that
![]()
There is also a straightforward definition for K′ ◦s, a φ if K′ ≽ = K that suffices for the theorem. If φ ∉ K′, then K′ ◦s, a φ = Cl(K ∪{φ}); if φ ∈ K′, then K′ ◦s, a φ = Cl({φ}).
The hard part is to define K ◦s, a φ if sa φ is not a local state in 퓙. The idea is to use (9.6) as much as possible. The definition splits into a number of cases:
-
There exists some formula φ′ such that sa φ′ is a local state in 퓙 and ⊨
 φ′ ⇒ φ. By REV3,
φ′ ⇒ φ. By REV3,  [sa] ∩
[sa] ∩  [φ′] ∈
[φ′] ∈  ′. Since
′. Since  ′ is closed under supersets, it follows that
′ is closed under supersets, it follows that  [sa] ∩
[sa] ∩  [φ] ∈
[φ] ∈  ′. Define
′. Define
By REV3, this would be equivalent to (9.6) if sa φ were a state. Note that the definition is independent of φ′; the fact that there exists φ′ such that ⊨
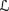 φ′ ⇒ φ is used only to ensure that
φ′ ⇒ φ is used only to ensure that  [sa] ∩
[sa] ∩  [φ] ∈
[φ] ∈  ′.
′. -
There exists some formula φ′ such that sa φ′ is a local state in 퓙, ⊨
 φ ⇒ φ′, and φ ∉ Bel(퓙, sa φ′). Since φ ∉ Bel(퓙, sa φ′), it follows that Pla(
φ ⇒ φ′, and φ ∉ Bel(퓙, sa φ′). Since φ ∉ Bel(퓙, sa φ′), it follows that Pla( [φ] |
[φ] |  [sa φ′]) > ⊥. By REV3,
[sa φ′]) > ⊥. By REV3,  [sa] ∩
[sa] ∩  [φ′] ∈
[φ′] ∈  ′ and P1a(
′ and P1a( [φ] |
[φ] |  [sa φ′]) = P1a(
[sa φ′]) = P1a( [φ] |
[φ] |  [sa] ∩
[sa] ∩  [φ′]) > ⊥. By BCS2,
[φ′]) > ⊥. By BCS2,  [sa] ∩
[sa] ∩  [φ] =
[φ] = 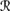 [sa] ∩
[sa] ∩ 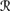 [φ] ∈
[φ] ∈ 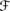 ′. That means K ◦s, a φ can again be defined using (9.7).
′. That means K ◦s, a φ can again be defined using (9.7). -
If sa φ′ is not a state in 퓙 for any formula φ′ such that ⊨
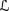 φ′ ⇒ φ or ⊨
φ′ ⇒ φ or ⊨ φ ⇒ φ′, then define K ◦s, a φ in the same way as K′ ◦s, a φ for K′ ≠ K. If φ ∉ K, then K ◦s, a φ = Cl(K ∩{φ}); if φ ∈ K, the K ◦s, a φ = Cl({φ}).
φ ⇒ φ′, then define K ◦s, a φ in the same way as K′ ◦s, a φ for K′ ≠ K. If φ ∉ K, then K ◦s, a φ = Cl(K ∩{φ}); if φ ∈ K, the K ◦s, a φ = Cl({φ}).
It remains to show that this definition satisfies R1–8. I leave it to the reader to check that this is the case if K ≢ Bel(퓙, sa) or sa φ is not a local state in 퓙 (Exercise 9.12), and I focus here on the case that K = Bel(퓙, sa), just to make it clear why REV1–3, BCS2, and BCS3 are needed for the argument.
-
R1 is immediate from the definition.
-
R2 follows from BCS3.
-
For R3, it suffices to show that if ψ ∈ Bel(퓙, sa φ) then ψ φ ∈ Bel(퓙, sa), for then ψ ∈ C1(K ∩ {φ}), by simple propositional reasoning. If ψ ∈ Bel(퓙, sa φ), then P1a(
 [ψ] |
[ψ] |  [sa φ]) > P1a(
[sa φ]) > P1a( [ ψ] |
[ ψ] |  [sa φ]). It follows from REV3 that P1a(
[sa φ]). It follows from REV3 that P1a( [ψ] |
[ψ] |  [sa] ∩
[sa] ∩  [φ]) > P1a(
[φ]) > P1a(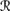 [ ψ] |
[ ψ] | 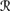 [sa] ∩
[sa] ∩ 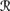 [φ]). Now there are two cases. If P1a(퓙[φ] |
[φ]). Now there are two cases. If P1a(퓙[φ] | 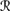 [sa]) > ⊥, then by CPl5, it immediately follows that
[sa]) > ⊥, then by CPl5, it immediately follows that
Now CPl3 gives
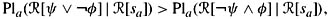
and it follows that ψ ∨ φ ∈ K. On the other hand, if P1(
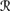 [φ] |
[φ] | 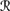 [sa]) = ⊥, then by Pl5 (which holds in 퓙, by BCS2) and CPl2, it follows that P1(
[sa]) = ⊥, then by Pl5 (which holds in 퓙, by BCS2) and CPl2, it follows that P1(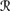 [ φ] |
[ φ] | 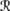 [sa]) = ⊥. (For if P1(
[sa]) = ⊥. (For if P1(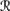 [ φ] |
[ φ] | 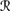 [sa]) = ⊥, then Pl5 implies that P1(
[sa]) = ⊥, then Pl5 implies that P1(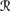 [ φ] ∪
[ φ] ∪  [φ] |
[φ] |  [sa]) = P1(
[sa]) = P1( |
|  [sa]) = ⊥, contradicting CPl2.) Thus,
[sa]) = ⊥, contradicting CPl2.) Thus,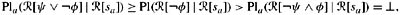
so again, ψ ∨ φ ∈ K.
-
For R4, REV2 comes into play. Suppose that φ ∉ K. To show that Cl(K ∪ {φ}) ⊆ K ◦s, a φ, it clearly suffices to show that K ⊆ K ◦s, a φ, since by R2, φ ∈◦s, a φ, and by R1, K ◦s, a φ is closed. Thus, suppose that ψ ∈ K = Bel(퓙, sa). Thus, P1a(
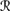 [ψ] |
[ψ] | 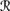 [sa]) > P1a(
[sa]) > P1a(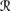 [ ψ] |
[ ψ] |  [sa]). By Pl6, P1a(
[sa]). By Pl6, P1a( [ψ ∧ φ] |
[ψ ∧ φ] |  [sa]) > P1a(
[sa]) > P1a( [ψ ∧ φ] |
[ψ ∧ φ] | 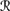 [sa]). Since φ ∈ K, it must be the case that P1a(
[sa]). Since φ ∈ K, it must be the case that P1a(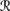 [φ] |
[φ] | 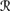 [sa]) > ⊥, so by CPl5, it follows that P1a(
[sa]) > ⊥, so by CPl5, it follows that P1a(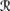 [ψ] |
[ψ] | 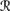 [sa]) ∩
[sa]) ∩ 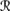 [φ]) > P1a (
[φ]) > P1a (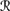 [ ψ] |
[ ψ] | 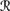 [sa] ∩
[sa] ∩ 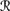 [φ]). Now REV3 gives
[φ]). Now REV3 gives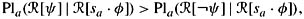
so ψ ∈ K ◦s, a φ, as desired.
-
For R5, note that if sa φ is a local state in 퓙, by BCS3, φ is consistent (i.e., it cannot be the case that ⊨
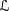 φ), and so is K ◦s, a φ.
φ), and so is K ◦s, a φ. -
R6 is immediate from the definition and Lemma 9.3.4.
-
The arguments for R7 and R8 are similar in spirit to those for R3 and R4; I leave the details to the reader (Exercise 9.12). Note that there is a subtlety here, since it is possible that s φ is a local state in 퓙 while s (φ ∧ ψ) is not, or vice versa. Nevertheless, the definitions still ensure that everything works out.
Theorem 9.3.5 is interesting not just for what it shows, but for what it does not show. Theorem 9.3.5 considers a fixed local state sa in 퓙 and shows that there is a belief revision operator ◦sa characterizing belief change from sa. It does not show that there is a single belief revision operator characterizing belief change in all of 퓙. That is, it does not say that there is a belief revision operator ο퓙 such that Bel(퓙, sa) ο퓙 φ = Bel(퓙, sa φ), for all local states sa in 퓙. This stronger result is, in general, false. That is because there is more to a local state than the beliefs that are true at that state. The following example illustrates this point:
Example 9.3.6
Consider a BCS 퓙 = (![]() ,
, ![]()
![]() , π) such that the following hold:
, π) such that the following hold:
-
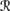 = {r1, r2, r3, r4}.
= {r1, r2, r3, r4}. -
π is such that p1 ∧ p2 is true throughout r1, p1 ∧ p2 is true throughout r2; and p1 ∧ p2 is true throughout r3 and r4.
-
In r1, the agent observes p1 and then p2; in r2, the agent observes p2 and then p1; in r3, agent observes p1 and then p2; and in r4, the agent observes p2 and then p1.
-
 is determined by a prior Pla on runs, where
is determined by a prior Pla on runs, where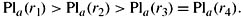
It is easy to check that 퓙 ∈ ![]()
![]()
![]() (Exercise 9.13). Note that Bel(퓙, 〈〉) = Bel(퓙 〈p1〉) = Cl(p1 ∧ p2), since p1 ∧ p2 is true in the unique most plausible run, r1, and in r1, the agent initially observes p1. Similarly, Bel(퓙, 〈 p2〉) = C1( p1 ∧ p2), since r2 is the unique most plausible run where the agent observes p2 first, and Bel(퓙, 〈p1, p2〉) = C1( p1 ∧ p2). Suppose that there were a revision operator ◦ such that Bel(퓙, sa) ο φ = Bel(퓙, sa φ) for all local states sa. It would then follow that Bel(퓙, 〈p2〉) = Bel(퓙, 〈p1, p2〉). But this is clearly false, since p1 ∈ Bel(퓙, 〈p2〉) and p1 ∉ Bel(퓙, 〈p1, p2〉).
(Exercise 9.13). Note that Bel(퓙, 〈〉) = Bel(퓙 〈p1〉) = Cl(p1 ∧ p2), since p1 ∧ p2 is true in the unique most plausible run, r1, and in r1, the agent initially observes p1. Similarly, Bel(퓙, 〈 p2〉) = C1( p1 ∧ p2), since r2 is the unique most plausible run where the agent observes p2 first, and Bel(퓙, 〈p1, p2〉) = C1( p1 ∧ p2). Suppose that there were a revision operator ◦ such that Bel(퓙, sa) ο φ = Bel(퓙, sa φ) for all local states sa. It would then follow that Bel(퓙, 〈p2〉) = Bel(퓙, 〈p1, p2〉). But this is clearly false, since p1 ∈ Bel(퓙, 〈p2〉) and p1 ∉ Bel(퓙, 〈p1, p2〉).
Example 9.3.6 illustrates a problem with the assumption implicit in AGM belief revision, that all that matters regarding how an agent revises her beliefs is her belief set and what is learned. I return to this problem in the next section.
Theorem 9.3.5 shows that for every BCS 퓙 ∊ ![]() ε
ε![]() and local state sa, there is a revision operator characterizing belief change at sa. The next result is essentially a converse.
and local state sa, there is a revision operator characterizing belief change at sa. The next result is essentially a converse.
Theorem 9.3.7
Let ◦ be a belief revision operator satisfying R1–8 and let K ⊆ ![]() e be a consistent belief set. Then there is a BCS 퓙K in
e be a consistent belief set. Then there is a BCS 퓙K in ![]() ∊
∊![]() such that Bel(퓙K, 〈〉) = K and
such that Bel(퓙K, 〈〉) = K and
K ◦ φ =Bel(퓙K, 〈φ〉)
for all φ ∊ ![]() e.
e.
Proof See Exercise 9.14.
Notice that Theorem 9.3.7 considers only consistent belief sets K. The requirement that K be consistent is necessary in Theorem 9.3.7. The AGM postulates allow the agent to "escape" from an inconsistent belief set, so that K ◦ φ may be consistent even if K is inconsistent. Indeed, R5 requires that it be possible to escape from an inconsistent belief set. On the other hand, if false ∊ Bel(퓙K, sa for some state sa and ra(m) = sa, then Pl(r, m)(W(r, m)) = ⊥. Since updating is done by conditioning, Pl(r, m+1)(W(r, m+1)) = ⊥, so the agent's belief set will remain inconsistent no matter what she learns. Thus, BCSs do not allow an agent to escape from an inconsistent belief set. This is a consequence of the use of conditioning to update.
Although it would be possible to modify the definition of BCSs to handle updates of inconsistent belief sets differently (and thus to allow the agent to escape from an inconsistent belief set), this does not seem so reasonable to me. Once an agent has learned false, why should learning something else suddenly make everything consistent again? Part of the issue here is exactly what it would mean for an agent to learn or discover false. (Note that this is very different from, say, learning p and then learning p.) Rather than modifying BCSs, I believe that it would in fact be more appropriate to reformulate R5 so that it does not require escape from an inconsistent belief set. Consider the following postulate:
R5*. K ◦ φ = Cl(false) iff ![]() φ or false ∊ K
φ or false ∊ K
If R5 is replaced by R5*, then Theorem 9.3.7 holds even if K is inconsistent (for trivial reasons, since in that case K ◦ φ = K for all φ). Alternatively, as I suggested earlier, it might also be reasonable to restrict belief sets to being consistent, in which case R5 is totally unnecessary.
|
EAN: 2147483647
Pages: 140