7.4 Reasoning about Other Quantitative Representations of Likelihood

The language ^QU_n is appropriate not just for reasoning about probability, but also for reasoning about lower probability, inner measure, belief, and possibility. That is, formulas in this language can be interpreted perfectly well in a number of different types of structures. All that changes is the class of structures considered and the interpretation of ℓ. Again, at the risk of boring the reader, I summarize the details here.

Much like the case of probability, lower probability structures, belief structures, and possibility structures have the form (W, X₁, …, X_n, π), where X_i(w) = (W_w,i_w,i, X_w,i). As expected, for lower probability, X_w_{, i} is a set of probability measures on _w,i; for belief structures, X_w_{, i} is a belief function on all subsets of w_w_{, i}; and for possibility structures, X_w_{, i} is a possibility measure on all subsets of w_w_{, i}. (Recall that for belief functions and possibility measures, I assumed that all sets were measurable.) Let ^lp_n, ^bel_n, and ^poss_n denote the denote the class of all lower probability structures, belief structures, and possibility structures, respectively, for n agents.

It is straightforward to define a notion of satisfaction for formulas in ^QU_n for all these structures as well as for ^prob_n, the set of arbitrary probability structures (where not all sets are necessarily measurable). In the latter case, ℓ_i is interpreted as "inner measure," rather than "probability."

In a lower probability structure M = (W, 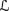풫₁,…, 풫_n, π),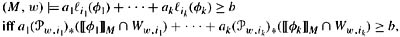

where 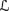풫_i(w) = (W_w,i, 풫_w,i) for i = 1, …, n. Thus, ℓ is now being interpreted as a lower probability. It could equally well have been interpreted as an upper probability; since lower probability is definable from upper probability, and vice versa (Equation 2.11), the choice is essentially a matter of taste.
In a belief structure M = (W, BE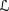₁, …, BE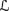_n, π),

where BE_i (w = (W_w,i, Bel_w,i) for i = 1, …, n.
In a probability structure M = (W, 풫₁,…, 풫_n) where not all sets are necessarily measurable, ℓ is interpreted as an inner measure, so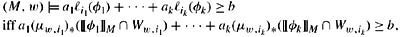

where 풫_i(w) = (W_w,i, _w,i, μ_w,i) for i = 1, …, n. This is a generalization of the measurable case; if all sets are in fact measurable, then the inner measure agrees with the measure. Again, it is possible to use outer measure here instead of inner measure; no new difficulties arise.
Finally, in a possibility structure M = (W, 풫OSS₁, …, 풫 OSS_n, π), ℓ is interpreted as a possibility measure, so

where 풫OSS_i(w) =(W_w,i, Poss_w,i) for i = 1, …, n.

Can these notions of uncertainty be characterized axiomatically? Clearly all the axioms and inference rules other than QU3 (finite additivity) are still valid in ^lp_n, ^bel_n, and ^prob_n In the case of ^bel_n, there is an obvious replacement for QU3: the analogues of B1 and B3.

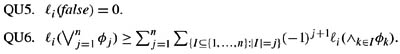
It turns out that QU1, QU2, QU5, QU6, together with Prop, MP, QUGen, and Ineq, give a sound and complete axiomatization for reasoning about belief functions. This is not so surprising, since the key axioms just capture the properties of belief functions in an obvious way. What is perhaps more surprising is that these axioms also capture reasoning about inner measures. As I observed in Section 2.4, every inner measure is a belief function, but not every belief function is an inner measure. This suggests that, although inner measures satisfy the analogue of B3 (namely, (2.8)), they may satisfy additional properties. In a precise sense, the following theorem shows they do not. Let AX^bel_n consist of QU1, QU2, QU5, QU6, QUGen, Prop, MP, and Ineq.

Theorem 7.4.1

AX^bel_n is a sound and complete axiomatization with respect to both ^bel_n and ^prob_n for the language ^QU_n

Proof Soundness is again straightforward (Exercise 7.9), and completeness is beyond the scope of this book. However, Exercises 7.10 and 7.11 explain why the same axioms characterize belief structures and probability structures, even though not every belief function is an inner measure. Roughly speaking, these exercises show that a formula is satisfiable in a belief structure if and only if it is satisfiable in a probability structure. Since every probability measure is a belief function, one direction is almost immediate. For the opposite direction, the key step is to show that, given a belief function Bel on W, it is possible to embed W in a larger space W′ and to define a measure μ on W′ such that μ* and Bel agree on the sets definable by formulas; see Exercise 7.11 for details.

For possibility structures, QU6 must be replaced by the key axiom that characterizes possibility, namely, that the possibility of a union of two disjoint sets is the max of their individual possibilities. The following axiom does the job:

QU7. (ℓ_i(Φ ∧ ψ) ≥ ℓ_i(Φ ∧ ψ)) ⇒ ℓ_i(Φ) = ℓ_i(Φ ∧ ψ).
Let AX^poss_n consist of QU1, QU2, QU5, QU7, QUGen, Prop, MP, and Ineq.

Theorem 7.4.2

AX^poss_n is a sound and complete axiomatization with respect to ^poss_n for the language ^QU_n.

What about lower probability? As was observed earlier (Exercise 2.14), lower probabilities do not satisfy the analogue of B3. It follows that QU6 is not valid in ^lp_n All the other axioms in AX^bel_n are valid though (Exercise 7.12). Since lower probabilities are superadditive (Exercise 2.14), the following axiom is also valid in ^lp_n:

However, this does not give a complete axiomatization. Recall from Section 2.3 that the following property holds for inner and outer measures:

Moreover (Exercise 2.15), this property does not follow from the superadditivity of lower probabilities. Thus, the axiom corresponding to this property is valid in ^lp_n and does not follow from the other axioms. There is a property given by (2.13) in Chapter 2 that characterizes lower probabilities. Consider the following axiom:

Note that if φ ⇔ ∨_{J⊆{1, …, k,}} _|J⊨m+n ∧_j∊Jφ_j and φ ⇔ ∨_{J⊆{1, …, k}}, _{|J ⊨m} ∧_j∊J φ^j are propositional tautologies, then in any structure M = (W, 풫₁,…,풫_n), the sets [[φ₁]]_M, …, [[φ_m]]_M must cover [[φ]]_M exactly m + n times and must cover [[ φ]]_M exactly m times. The soundness of QU8 in ^lp_n now easily follows from (2.13) (Exercise 7.13). Moreover, QU8 is just what is needed to get completeness. Let AX^lp_n consist of QU1, QU2, QU5, QU8, QUGen, Prop, MP, and Ineq. (That is, AX^lp_n is the result of replacing QU7 in AX^poss_n by QU8.)

Theorem 7.4.3

AX^lp_n is a sound and complete axiomatization with respect to ^lp_n for the language ^QU_n.