6.1 Epistemic Frames

Before dealing with many agents, consider the single-agent case again. Starting with Section 2.1, an agent's uncertainty has been represented by a single set W of possible worlds. In general, however, the set of worlds an agent considers possible depends on the actual world. To take a trivial example, the set of worlds the agent considers possible when it is raining is clearly different from the set of worlds the agent considers possible when it is sunny.

The dependence of the set of possible worlds on the actual world can be modeled using (epistemic) frames. ("Epistemic" means "of or pertaining to knowledge or the conditions for acquiring it.") An epistemic frame F is a pair (W, ), where, as before, W is a set of possible worlds. The new feature here is the . is a binary relation on W (sometimes called a possibility relation or accessibility relation), that is, a subset of W W. Intuitively, (w, w′) ∈ if the agent considers w′ a possible world in world w. Define (w) = {w′:(w, w′) ∈ }; (w) is the set of worlds that the agent considers possible in world w. Although taking to be a binary relation is more standard in the literature, viewing as a function from worlds to sets of worlds will often turn out to be more convenient.

Now the question of whether an agent considers an event possible or knows an event depends on the world. An agent considers U possible at world w (in an epistemic frame F) if U ∩ (w) ≠ (∅); the agent knows U at world w if (w) ⊆ U. Put another way, the agent knows U if every world she considers possible is in U.

There are various natural constraints that can be placed on the relation; these constraints capture some standard assumptions about the agent's possibility relation. For example, if the agent always considers the actual world possible, then (w, w) ∈ for all w ∈ W, that is, is reflexive. Similarly, it may be appropriate to assume that if (u, v) and (v, w) are both in (so that w is considered possible in world v, and w is considered possible in v) then (u, w) ∈ (so that w is considered possible in u). This just says that is transitive. There are many other constraints that could be placed on . I mention some other standard ones here.

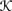is Euclidean if (u, v), (u, w) ∈ 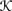implies (v, w) ∈ 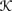, for all u, v, w ∈ W.
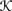is symmetric if (u, v) ∈ 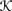implies that (v, u) ∈ 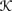for all u, v, ∈ W.
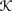is serial if for all w ∈ W, there is some w′ ∈ W such that (w, w′) ∈ 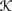. This just says that the agent always considers some world possible.
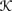is an equivalence relation if it is reflexive, symmetric, and transitive. It is easy to see that this is equivalent to being reflexive, Euclidean, and transitive (Exercise 6.1).

Note that these constraints have natural interpretations if is viewed as a function from worlds to sets of worlds. In particular, is reflexive iff w ∈ (w) for all worlds w; is transitive iff, for all worlds w and w′, if w′ ∈ (w) then (w′) ⊆ (w); and is Euclidean iff, for all worlds w, w′, if w′ ∈ (w), then (w′) ⊇ (w) (Exercise 6.2). It follows that if is Euclidean and transitive, then (w′) = (w) for all w′ ∈ (w); the set of worlds that the agent considers possible is then the same in all worlds that she considers possible (and thus can be viewed as being independent of the actual world). Reflexivity is the property taken to distinguish knowledge from belief; I discuss belief in Section 8.1 and Chapter 9. In many applications, the relation is naturally viewed as being an equivalence relation, which makes it reflexive, Euclidean, and transitive.

Epistemic frames can easily be generalized to accommodate many agents. There is then one possibility relation for each agent. Formally, an epistemic frame F for n agents is a tuple (W, ₁, …, _n), where each _i is a binary relation on W. _i(w) should be thought of as the set of worlds that agent i considers possible at world w. In general, _i(w) will be different from _j(w) if i ≠ j. Different agents will consider different worlds possible.

One of the advantages of an epistemic frame is that it can be viewed as a labeled graph, that is, a set of labeled nodes connected by directed, labeled edges. The nodes are the worlds in W, and there is an edge from w to w′ labeled i exactly if (w, w′) ∈ _i. The graphical viewpoint makes it easier to see the connection between worlds. Consider the following example:

Example 6.1.1

Suppose that a deck consists of three cards labeled A, B, and C. Agents 1 and 2 each get one of these cards; the third card is left face down. A possible world is characterized by describing the cards held by each agent. For example, in the world (A, B), agent 1 holds card A and agent 2 holds card B (while card C is face down). There are clearly six possible worlds: (A, B), (A, C), (B, A), (B, C), (C, A), and (C, B). In the world (A, B), agent 1 thinks two worlds are possible: (A, B) itself and (A, C). Agent 1 knows that he has card A but considers it possible that agent 2 could hold either card B or card C. Similarly, in world (A, B), agent 2 also considers two worlds: (A, B) and (C, B). In general, in a world (x, y), agent 1 considers (x, y) and (x, z) possible, while agent 2 considers (x, y) and (z, y) possible, where z is different from both x and y.

From this description, the ₁ and ₂ relations can easily be constructed. It is easy to check that they are equivalence relations. This is because an agent's knowledge is determined by the information he has, namely, the card he is holding. (Considerations similar to these lead to the use of equivalence relations in many examples involving knowledge.) The frame is described in Figure 6.1, where, since the relations are equivalence relations, I omit the self loops and the arrows on edges for simplicity (if there is an edge labeled i from state w to state w′, there has to be an edge labeled i from w′ to w as well by symmetry).

Notice how important it is to include in the frame worlds that both agents know to be impossible. For example, in the world (A, B), both agents know perfectly well that the world (B, A) cannot be the case (after all, agent 1 knows that his own card is A, not B, and agent 2 knows that her card is B, not A). Nevertheless, because agent 1 considers it possible that agent 2 considers it possible that agent 1 considers it possible that (B, A) is the case, (B, A) must be included in the frame. The fact that both agents consider (B, A) impossible in situation (A, B) is captured in the frame by the fact that there is no edge from (A, B) to (B, A); the fact that agent 1 considers it possible that agent 2 considers it possible that agent 1 considers it possible that (B, A) is the case is captured by the path from (A, B) to (B, A) consisting of three edges, labeled 1, 2, and 1, respectively.

Notice that, in this frame, in the world (A, B), agent 1 knows that agent 2 holds either the B or C (since agent 1 considers two worlds possible, (A, B) and (A, C), and in both of them, agent 2 holds either the B or the C). At world (A, B), agent 1 also knows that agent 2 does not know that agent 1 has card A. That is because in each of the two worlds that agent 1 considers possible, agent 2 does not know that agent 1 has card A. In world (A, B), agent 2 considers it possible that agent 1 has card C (since agent 2 considers world (C, B) possible), and in world (A, C), agent 2 considers it possible that agent 1 has card B.

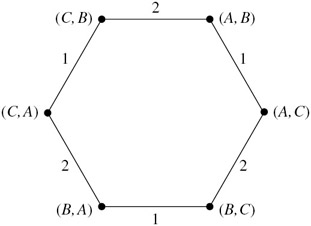
click to expand
Figure 6.1: An epistemic frame describing a simple card game.

At least in this simple setting, the formal definition of knowledge seems to capture some of the intuitions usually associated with the word "knowledge." The examples in the rest of this chapter provide further justification, as does the axiomatic characterization of knowledge given in Section 7.2.3.