Exercises

• 3.1 Show that both CP4 and CP5 follow from CP3 (and CP1 in the case of CP4); in addition, CP3 follows immediately from CP4 and CP5.

• 3.2 Show that μ^s as defined in Section 3.2 satisfies CP1–3.

• 3.3 Fill in the missing details in the proof of Theorem 3.2.5.

• * 3.4 Prove Theorem 3.2.6.

• 3.5 Show that (aα² + (1 − a)β²)/(aα + (1 − a)β) ≥ aα + (1 − a)β, with equality holding iff α = β, a = 1, or a = 1. (Hint: This amounts to showing that (aα (1 − a)β²) ≥ (aα + (1 − a)β)². Let f(a) = aα² + (1 − a)β²) − (aα + (1 − a)β)². Clearly, f(0) = f(1) = 0. Show, using calculus, that f(a) > 0 for 0 < a < 1.)

• 3.6 In Example 3.4.1, prove that μ(C_α | H¹) > a, using the fact that α > β.

• 3.7 Prove Proposition 3.4.3.

• 3.8 Prove Proposition 3.4.4.

• 3.9 Show that Bel_o is a belief function and it has the property that Plaus_o(h) = cμ_h(o) for some constant c > 0.

• * 3.10 Prove Theorem 3.4.5.

• * 3.11 Prove Theorem 3.4.6.

• * 3.12 Prove the converse of Theorem 3.4.5. That is, show that if Bel captures the evidence o, then Plaus(h) = cμ_h(o) for some constant c > 0 and all h ∊ .

• 3.13 Fill in the following missing details in the proof of Theorem 3.5.1.

  1. Show that if x + y > 0, y ≥ 0, and x ≤ x′, then x/(x + y) ≤ x′/(x′ + y).

  2. Show that there exists an extension μ₁ of μ such that

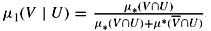
  3. Do the argument for μ*(V | U).

• 3.14 Show that if U is measurable, then

  

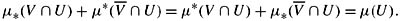
• 3.15 Prove Theorem 3.6.2. You may use results from previous exercises.

• 3.16 Show that Plaus(V | U) = 1 − Bel(V |U).

• 3.17 Construct a belief function Bel on W = {a, b, c} and a set ≠ _Bel of probability measures such that Bel = _* and Plaus = * (as in Exercise 2.24) but Bel|{a, b} ≠ (|{a, b}_*).

• 3.18 Prove Proposition 3.6.5.

• 3.19 Show that if Bel is a probability measure μ, then Bel(V | U) = Bel(V ||U) = μ(V | U); that is, both notions of conditioning belief functions agree with conditioning for probability.

• * 3.20 Show that Plaus(U) ≥ Plaus(V ∩ U) + Bel(V ∩ U). (Hint: Use Theorem 2.4.1 and observe that μ′(U) ≥ μ′(V ∩ U) + Bel(V ∩ U) if μ′ ∊ _Bel.)

• 3.21 If Poss(U) > 0, show that Poss( ||U) is a possibility measure.

• 3.22 Show that if Poss is a possibility measure on W = {w₁, w₂, w₃} such that Poss(w₁) = 2/3, Poss(w₂) = 1/2, and Poss(w₃) = 1, U = {w₁, w₂}, and V = {w₁}, then, for all α ∈ [2/3, 1], there is a conditional possibility measure Poss_α on W that is an extension of Poss (i.e., Poss_α|W = Poss) and satisfies CPoss1–4 such that Poss(V | U) = α.

• 3.23 Given an unconditional possibility measure Poss, show that the conditional possibility measure defined by (3.6) satisfies CPoss1–4. Moreover, show that among conditional possibility measures defined on 2^W ′, where 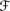′ = {U : Poss(U) > 0}, it is the largest standard conditional possibility measure extending Poss that satisfies CPoss1–4. That is, show that if Poss′ is another conditional possibility measure defined on 2^W 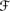′ that satisfies CPoss1–4, and Poss′( |W) = Poss, then Poss(V | U) ≥ Poss′(V | U) for all sets V.

• 3.24 Show that Poss(V | U) is not determined by Poss(U | V), Poss(U), and Poss(V). That is, show that there are two possibility measures Poss and Poss′ on a space W such that Poss(U | V) = Poss′(U | V), Poss(U) = Poss′(U), Poss(V) = Poss′(V), but Poss(V | U) ≠ Poss′(V | U).

• 3.25 Show that the unique conditional ranking function extending an unconditional ranking function κ defined on 2^W 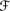′, where 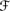′ = {U : κ (U) ≠ ∞}, and satisfying CRk1–4 is given by (3.7).

• 3.26 Show that if (W, 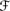, 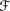′, Pl) is such that (a)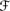 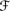′ is a Popper algebra of subsets of W W, (b) Pl: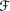 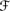′ → D for some partially ordered D of values and satisfies CPl1, CPl2, CPl3, and CPl5, and (c) U ∊ 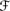′ and Pl(V | U) > ⊥ implies that V ∩ U ∊ 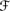, then Pl satisfies CPl4.

• 3.27 Show that all conditional probability measures satisfy CPl5, as do the conditional possibility measures (both Poss( |U) and Poss( ||U)) and conditional ranking functions obtained by the constructions in Section 3.7 and Section 3.8, respectively. However, show that _*(.|U), Bel(.|U), and Bel( ||U) do not in general satisfy CPl5.

• 3.28 Given a set of probability measures defined on an algebra , let ′ = {U : μ (U) ≠ 0 for all μ ∊ }. Extend Pl to ′ by defining Pl (V | U) = f_V|U where f_V|U(μ) = μ(V | U). Show that Pl so defined gives a cps satisfying CPl5, but one that is not in general acceptable.

• 3.29 Show that the construction of a conditional plausibility measure starting from the unconditional plausibility measure Pl representing a set of probability measures results in an acceptable cps satisfying CPl5 that is an extension of Pl.

• 3.30 Show that the construction of a conditional plausibility measure starting from an unconditional plausibility measure Pl results in an acceptable cps satisfying CPl5 that is an extension of Pl.

• 3.31 Show that Alg1–4 hold for probability (with + and for ⊕ and ⊗), as well as for Poss(V ||U), with max and for ⊕ and ⊗, and κ(V | U), with min and + for ⊕ and ⊗.

• 3.32 Show that Alg1–3 hold for Poss(V | U).

• 3.33 Show that the cps defined from Pl 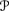satisfies Alg1–4.

• 3.34 Prove Lemma 3.9.3.

• 3.35 Prove Lemma 3.9.4.

• 3.36 Prove Lemma 3.9.5.

• 3.37 Given an algebraic cps, say that ⊗ is monotonic if d ≤ d′ and e ≤ e′ implies d ⊗ e ≤ d′ ⊗ e′.

  1. Show that all the constructions that give algebraic cps's discussed in Section 3.9 actually give monotonic cps's.

  2. Show that a cps that is standard, algebraic, and monotonic satisfies CPl5.

• 3.38 Prove Lemma 3.9.6.

• 3.39 Show that property J2 of Jeffrey conditioning is a consequence of property J.

• 3.40 Show that μ|(α₁U₁;…; α_nU_n) is defined as long as μ(U_j) > 0 if α_j > 0 and is the unique probability measure satisfying property J if it is defined.

• 3.41 Show that if μ(U₁ ∩ U₂) ≠ 0, then

  

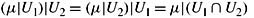
• 3.42 Show that Bel|(α₁U₁;…; α_nU_n) and Bel||(α₁U₁;…; α_nU_n) are belief functions (provided that Plaus(U_j) > 0 if α_j > 0). Show, however, that neither gives the same result as Dempster's Rule of Combination, in general. More precisely, given a belief function Bel and an observation α₁U₁;…; α_nU_n, let Bel_{α1U1;…;αnUn} be the belief function whose mass function puts mass α_j on the set U_j (and puts mass 0 on any set V ′∈{U₁, …, U_n}). Show by means of a counterexample that, in general, Bel ⊕ Bel_{α1U1;…;αnUn} is different from both Bel|(α₁U₁;…; α_nU_n) and Bel||(α₁U₁;…; α_nU_n).

• 3.43 Show that 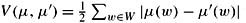. (Hint: Consider the set U = {w : μ(w) ≥ μ′(w)} and show that ∑_w∈U μ(w) − μ′(w) = ∑_w∈U μ′(w) − μ(w).)

• * 3.44 Suppose that U₁, …, U_n is a partition of W and α₁ + … + α_n = 1. Let C = {μ′ : μ′(U_i) = α_i, i = 1, …, n}. Suppose that μ′′ is a probability measure such that

  • μ′′ ∈ C,

  • if μ′′(U_i) < μ(U_i) then μ′′(w) < μ(w) for all w ∈ U_i, i = 1, …, n,

  • if μ′′(U_i) = μ(U_i) then μ′′(w) = μ(w) for all w ∈ U_i, i = 1, …, n,

  • if μ′′(U_i) > μ (U_i) then μ′′(w) > μ(w) for all w ∈ U_i, i = 1, …, n.

  Show that V(μ, μ′′) = inf{V(μ, μ′) : μ′ ∈ C}.

  Since μ|(α₁U₁;…; α_nU_n) clearly satisfies these four conditions, it has the minimum variation distance to μ among all the measures in C. However, it is clearly not the unique measure with this property.

• * 3.45 (This exercise requires calculus.) Show that D(μ′, μ) ≥ 0 (if it is defined), with equality coming only if μ′ = μ. (Hint: First show that x log(x) − x/ log_e(2) + 1/ log_e(2) ≥ 0 if x ≥ 0, with equality iff x = 1. Then note that

  

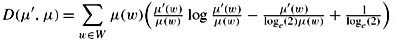
  The result easily follows.)

• 3.46 Show by means of a counterexample that D(μ, μ′) ≠ D(μ′, μ) in general.

• * 3.47 (This exercise requires calculus.) Show that of all probability measures on a finite space W, the one that has the highest entropy is the uniform probability measure. (Hint: Prove by induction on k the stronger result that for all c > 0, if x_i ≥ 0 for i = 1, …, k and ∑^k_{i = 1} x_i = c, then − ∑₌₁ x_i log(x_i) is maximized if x_i = c/k.)

• 3.48 (This exercise requires calculus.) Show that if C consists of the constraints μ′({blue, green}) = .8 and μ′({red, yellow}) = .2, then the measure μ^me that maximizes entropy is the one such that μ^me(blue) = μ^me(green) = .4 and μ^me(red) = μ^me(yellow) = .1.

• 3.49 Formulate an analogue of variation distance for possibility measures, and then prove an analogue of Proposition 3.11.1. Repeat this for ranking functions.

• * 3.50 Yet another representation of uncertainty is a lexicographic probability space (LPS). An LPS 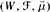consists of a set of worlds W, an algebra 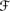over W, and a tuple 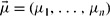of probability measures all defined on 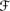, for some n ≥ 1. (For the purposes of this exercise, assume that n is finite, although the definition makes sense even if the length of the LPS is infinite.) Define 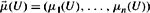. An LPS acts much like a set 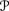of probability measures with one difference. Consider the lexicographic order on tuples in [0, 1]ⁿ defined by taking (a₁, …, a_n)<_LPS (b₁, …, b_n) iff there is some j ≤ n such that a_i = b_i for i < j and a_j < b_j. Define (μ₁, …, μ_n)(U) <_{LP S} (μ₁, …, μ_n)(V) if (μ₁(U), …, μ_n(U)) <_LPS (μ₁(V), …, μ_n(V)). Thus, the relative likelihood of U and V according to (μ₁, …, μ_n) is determined by looking at the first probability measure in the sequence that gives U and V different probabilities. The measures in the sequence (μ₁, …, μ_n) can be viewed as listed lexicographically, with μ₁ more significant than μ₂, μ₂ more significant than μ₃, and so on.

  Conditioning in LPSs is defined as follows. Given 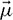and U ∊ 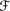such that μ_i(U) > 0 for some index i, let 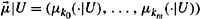where (k₀, …, k_m) is the subsequence of all indices j such that μ_j (U) > 0. Notice that the length of the LPS 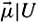depends on U.

  1. Find a set D and an ordering on D such that if 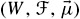is an LPS, then 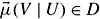for all U such that 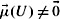. Moreover, show that with this choice of 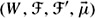is a cps that satisfies CPl1–5.

  2. Show that 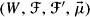is actually an algebraic cps, by defining appropriate notions of ⊕ and ⊗.

• 3.51 This exercise further examines lexicographic probability systems. The definition of conditioning in an LPS given in the previous exercise does not result in a cps in general, since (μ₁, …, μ_n)(W |W) is not equal to (μ₁, …, μ_n)(U | U) if, for example, μ₁(U) = 0 and μ₂(U) ≠ 0. Show how to modify this definition, along that lines used for PI, so as to give an algebraic cps. Carefully define Dom(⊗) and Dom(⊕).