5.1. Statistical Process Control
This chapter's example is a check processing
operation. The number of checks varies by day of the week as does
the amount of money deposited. These are measures of quantity and
can be forecasted and
monitored
using techniques in Chapter 3. But
quality is as important as quantity. If something is going wrong in
the operation (e.g., if payments are being misapplied, or check
numbers
are being recorded incorrectly), we need to know.
5.1.1. Choosing Metrics
When monitoring a manufacturing process we can
measure the diameter of a bolt, the weight of a
bottle
of shampoo,
or the percent of electrical
components
failing a test. These are
things that do not vary by day of the week, and a significant
change in any of them can mean trouble. In our check processing
operation we need to use metrics that behave this way.
First, we consider potential problem areas.
Checks received for payment need to be
processed
quickly, so we
measure the average age of the checks. Customers are supposed to
send a remittance slip with their check, and we will measure the
percentage of payments received that contain only a check and the
average number of pages of remittance information per check. Money
is important, so we measure both the average check amount and the
average amount per remittance page. Finally, we need to monitor the
accuracy of our data capture process. For this we look at the
percentage of checks that have a valid invoice number, the average
number of digits in the check number, and the average number of
digits in the check amount.
If any of these metrics shows a significant
change we need to find the reason. Avoiding metrics based on volume
or day of the week keeps the focus on quality.
This concept can be applied to almost any
operation. In a call center you might look at average talk time,
percentage of calls
abandoned
, and percentage of calls transferred.
In an
invoicing
area it could be average value, average lines, and
product mix.
5.1.2. X and S
Charts
The process, like forecasting, is simply
predicting what each metric should be, knowing how accurate the
prediction is, and using this to set control limits for each
metric. The prediction is the recent average. We don't consider lag
since these metrics are not cyclic. We don't correct for the trend.
If there is a trend, we want to know. We are looking for
trends.
We use two kinds of metrics. First is the
average. In the example we look at the average number of pages per
check. Second is the standard deviation. For some metrics we need
to know if the amount of variation is changing. With number of
pages per check, the average could be steady, yet we could be
getting more really high and low page counts.
Results are displayed on a chart like the one in
Figure 5-1.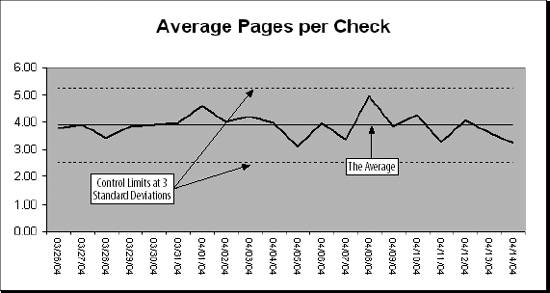
Charts dealing with averages are called
X
charts
. Those dealing with standard deviation are called
S
charts
. Years ago there were also charts that
looked
at the
range (the difference between the highest and
lowest
measurement).
They were called
R charts
, and were used because the
calculations are simpler. Finding standard deviations by hand for
hours every day is not as much fun as you might think.
Today the distinction between X and S charts
doesn't mean much. The terminology evolved before PCs and Excel.
Statistical Process Control was a complex and labor
intensive
proposition. The metrics had to be manually collected and the
calculations done by hand. Today you can probably collect all your
metrics from automated sources and Excel takes care of the
calculations.
The control limits are usually set three
standard deviations from the average. This means that 99.7 percent
of the time the metric will be within the control limits if there
is not a problem. This also means that three times in every
thousand tests there is a false positive.
Of course, you don't have to use three standard
deviations. Three is commonly used because it gives good results
and because that's what everyone else uses. But you can use a
different number. The number of standard deviations used to set the
control limits is called the sigma . It is a trade off. A low sigma
is good at detecting problems, but it is also good at producing
false positives. A high sigma means less work tracking down false
alarms but a better chance of missing something important.
We assume the metrics are normally distributed.
In the real world few things really are, but it is easier to assume
that they are normal than it is to figure out what is actually
going on. There are times, however, when a different distribution
gives better results.
The application will let the
user
choose to use
either a normal or
log normal
distribution
. In a log normal distribution, the measures
are skewed to the high end of the range. Using a log normal
distribution to set the limits makes the application more sensitive
to
drops
in the metric. It
improves
detection of
skipped
digit
problems. This can be helpful in monitoring keying or OCR
operations, for example.
|
