63.
5.2 Networks for Binary Addition
In this section, we review the half adder and full adder circuits and show how these can be cascaded to form adder circuits over multiple bits. These circuits have no difficulty working with the twos complement number scheme we described in the previous section.5.2.1 Half Adder/Full Adder
In this subsection, we reexamine the adder structures first introduced in Chapter 1.Half Adder The half adder is the most primitive of the arithmetic circuits. It has two inputs-the bits to be added-and two outputs-the sum and a carry-out.
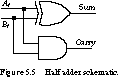
Figure 5.5 shows the schematic for the half adder.
Full Adder If we want to do multibit additions, a half adder isn't enough. When we do addition with pencil and paper, the carry from one column of digits is added to the sum of the column to its left. The same works for binary addition. We form the ith sum from the addition of the ith bits and the carry-out of the (i - 1)st sum.
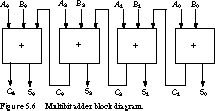
The idea is shown in Figure 5.6 for a 4-bit adder. The rightmost "adder slice" can be a half adder, but each of the adders to the left has three inputs: Ai, Bi, and the carry-out of the preceding stage. The best way to construct this multibit adder is to use a single building block that can be cascaded to form an adder of any number of bits: the full adder.
The full adder has three inputs-A, B, and CI (carry-in)-and two outputs-S (sum) and CO (carry-out). S is written as
while CO can be expressed in two-level and multilevel forms as
The implementation of the full adder suggested by the multilevel expressions is shown in Figure 5.7.
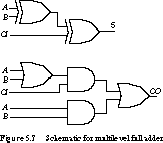
This implementation requires six gates.
In Chapter 1, we saw how to implement a full adder in terms of cascaded half adders. In this scheme, we need only five gates for this implementation of the full adder: two for each of the two half adders and one OR gate for the carry-out. This is one fewer than in Figure 5.7. However, with cascaded half adders, the carry output passes through three gate levels: an XOR (first-stage sum), an AND gate (second-stage carry), and a final stage OR gate (final carry). This compares with an OR, AND, OR path in Figure 5.7. Since an OR gate is considerably faster than an XOR gate in most technologies, the multiple half adder implementation is probably slower.
Adder/Subtractor
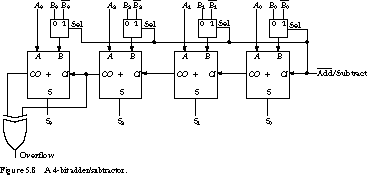
Figure 5.8 shows the circuit for a 4-bit adder/subtractor constructed from full adder building blocks. Besides the Ai and Bi inputs, we have introduced a control input 
. When this signal is 0, the circuit performs addition. When it is 1, the circuit becomes a subtractor.
The 
input feeds the low-order carry-in and the selection input of four 2:1 multiplexers. When it is asserted, the multiplexers deliver the complements of the Bi inputs to the full adders and set the low-order carry-in to 1. This is exactly the way to form 
, the sum of A and the twos complement negation of B.
The circuit includes an XOR gate whose inputs are the carry-in and carry-out of the highest-order (leftmost) adder stage. When these bits differ, an overflow has occurred. We use the XOR to signal that an overflow has taken place.
5.2.2 Carry Look-ahead Circuits
Carry look-ahead circuits are special logic circuits that can dramatically reduce the time to perform addition. We study them next.Critical Delay Paths in Adder Circuits The adder of Figure 5.8 sums the Ai and Bi bits in parallel. But for the Si outputs to be correct, the adder requires serial propagation of the carry outputs from the rightmost, lowest-order stage to the leftmost, highest-order stage. The "rippling" of the carry from one stage to the next determines the adder's ultimate delay.
Let's analyze the delays in the ripple adder by counting gate delays. We will assume that the adder stages are implemented as in Figure 5.7 and, for simplicity, that all gates have the same delay. At time 0 the inputs Ai, Bi, and C0 are presented to the adder. Within two gate delays, one delay for each XOR gate, S0 will be valid.
The carry signal is more complex, and we must examine it on a case-by-case basis. When Ai = Bi = 1, the carry is computed in two gate delays and is independent of the carry-in
(carry-out will always be 1 in this case). When Ai = Bi = 0, the carry is also valid after two gate delays and is still independent of the carry-in (carry-out will always be 0). When Ai ¦ Bi, the calculation of the carry takes three gate delays (carry-out depends on the carry-in). This is the base case for the zeroth bit. When adders are cascaded, the critical delay is the time to compute the carry-out after the arrival of a valid carry-in. If the carry-in arrives after N gate delays, the carry-out will be computed by time N + 2. This is shown in Figure 5.9(a).
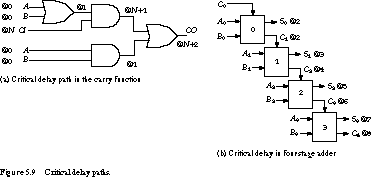
The @ notation indicates the number of gate delays before a given signal is valid.
Figure 5.9(b) shows the delays in the cascaded logic for the worst-case addition, 11112 + 00012, since each bit sum generates a carry into the next position. With the inputs arriving at time 0, the zeroth-stage sum and carry are generated at time 2. In the first stage, the sum is computed after one delay and the carry-out takes two. The valid carry-out of stage 1 at time 4 generates a valid sum and carry-out at times 5 and 6, respectively, for the third stage. This leads to a final stage sum and carry at times 7 and 8, respectively.
In general, the sum output from stage i, Si, will be valid after two gate delays if i = 0 and (2*i + 1) if i > 0. For i 0, the carry-out Ci + 1 will be valid one delay after the sum is valid.
Because this analysis assumes that each stage experiences the worst-case delay, it is often called the upper bound. The timing waveforms for the worst case are shown in Figure 5.10.
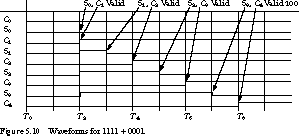
The actual delay depends on the particular pattern of the inputs. For example, for the 4-bit sum 01012 + 10102, the output will be valid after only two gate delays, since there are no carries between stages.
Although an eight-gate delay may not seem so bad for a 4-bit adder, the cascaded delays become intolerable for adders of greater widths, such as 32 or 64 bits. An 8-stage adder takes 16 gate delays, a 16-stage adder 32 gate delays, and a 32-stage adder 64 gate delays (to final stage carry-out) in the worst case. This observation led hardware designers to develop carry look-ahead schemes. These are ways to calculate the carry inputs in parallel rather than in series. We look at these next.
Carry Look-ahead Logic In the 4-bit "ripple" adder, the carry-out of each stage, Ci + 1, is expressed as a function of Ai, Bi, and Ci. The basic idea of carry look-ahead logic is to express each Ci in terms of Ai, Ai - 1, , A0, Bi, Bi - 1, , B0, and C0 directly. This is a much more complicated Boolean function, but it can always be expressed in two-level logic form. Thus, it should never take more than two gate delays to compute any of the carry outputs.
We begin by introducing two new functions from which we will construct the look-ahead carry. These are called carry generate, written Gi, and carry propagate, written Pi. They are defined as
In our previous analysis of the carry function, when Ai and Bi are both 1, a carry must be generated, independent of the carry-in. Hence, we call the function "carry generate." If one of Ai and Bi is 1 while the other is 0, then the carry-out will be identical to the carry-in. In other words, when the XOR is true, we pass or "propagate" the carry across the stage.
Interestingly, sum and carry-out can be expressed in terms of the carry generate and carry propagate functions:
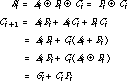
When the carry-out is 1, either the carry is internally generated within the stage (Gi) or the carry-in is 1 (Ci) and it is propagated (Pi) through the stage.
Expressed in terms of carry propagate and generate, we can rewrite the carry-out logic as follows:
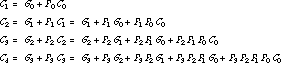
The ith carry signal is the OR of i + 1 product terms, the most complex of which has i + 1 literals. This places a practical limit on the number of stages across which the carry look-ahead logic can be computed. Four-stage look-ahead circuits are commonly available in parts catalogs and cell libraries. Eight-stage look-ahead circuits are difficult to find because of the scarcity of nine-input gates.
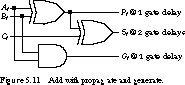
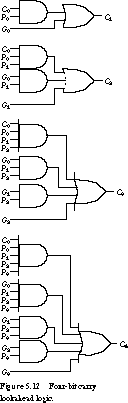
Implementing Carry Look-ahead Logic Figure 5.11 shows the schematic for an adder stage with propagate and generate outputs. The carry look-ahead circuits for a 4-bit adder are given in Figure 5.12. If the inputs to the 0th adder stage are available at time 0, it takes one gate delay to compute the propagate and generate signals and two gate delays to compute the sum. When the Pi and Gi are available, the subsequent carries, C1, C2, C3, and C4, are computed after two more gate delays (three gate delays total). The sum bits can be computed in just one more gate delay.
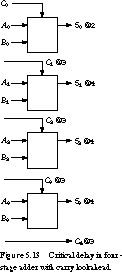
The cascaded delay for the 4-bit adder with carry look-ahead is shown in Figure 5.13. The final sum bit is available after four gate delays, compared with seven gate delays in the adder without carry look-ahead. This analysis assumes that five-input gates have the same delay as two-input gates, which is not usually the case. Based on this simplifying assumption, we have been able to cut the add time in half.
Direct calculation of the carry look-ahead logic beyond 4 bits becomes impractical because of the very high fan-ins that would be required. So how would we apply carry look-ahead techniques to something like a 16-bit adder?
We take a hierarchical approach. We can implement 16-bit sums with four 4-bit adders, each employing its own internal 4-bit carry look-ahead logic. Each 4-bit adder computes its own "group" carry propagate and generate: the group propagate is the AND of P3, P2, P1, P0, while the group generate is the expression 
.
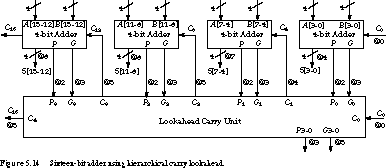
A second-stage circuit computes the look-aheads and the output carries between first-stage 4-bit adders. The logic is identical to that of Figure 5.12. Figure 5.14 shows the block diagram. The propagate and generate functions are computed from the inputs in just one gate delay. For each 4-bit adder, the group propagate incurs one more delay while the group generate incurs two delays. These signals are presented to the second-level carry look-ahead logic at times 2 and 3, respectively.
Once the carry-in to a 4-bit adder is known, the internal carry look-ahead logic computes the sums in four more gate delays for the lowest-order stage and three gate delays in the higher-order adder stages.
The zeroth stage takes longer because its sums must wait one gate delay for the propagates and generates to be computed in the first place. The other stages overlap the propagate and generate computations with the carry calculations in the external carry look-ahead unit. Given this reasoning, the sums for bits 3 through 0 are valid after four gate delays.
To the external second-level carry look-ahead, C0 arrives at time 0, Pi arrives at time 2, and Gi arrives at time 3. Using the schematics of Figure 5.12, C4 becomes valid at time 4, while C8, C12, and C16 become valid at time 5. The sums of the second, third, and fourth adder stages are computed in three more gate delays. Thus sum bits 7 through 4 become valid at time 7, while bits 15 through 8 are available at time 8.
So in eight delays we can calculate a 16-bit sum, compared with 32 delays in a simple 16-bit ripple adder. We can generalize the approach for adders spanning any number of inputs. For example, a 64-bit adder can be constructed from sixteen 4-bit adders, four 4-bit carry look-ahead units at the second level, and a single 4-bit carry look-ahead unit at the third level.
5.2.3 Carry Select Adder
The circuits of the last subsection trade more gates and hardware complexity for a faster method to compute the interstage carries. In this section, we examine the carry select adder, an adder organization that introduces redundant hardware to make the carry calculations go even faster.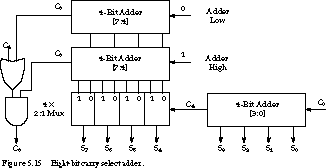
Figure 5.15 illustrates the concept by showing the organization of an 8-bit carry select adder. The 8-bit adder is split in half. The upper half is implemented by two independent 4-bit adders, one whose carry-in is hardwired to 0 ("adder low"), another whose carry-in is hardwired to 1 ("adder high"). In parallel, these compute two alternative sums for the higher-order bits. The carry-out of the lower-order 4-bit adder controls multiplexers that select between the two alternative sums.
The circuit for C8 could be a 2:1 multiplexer, but a simpler circuit that reduces the gate count also does the job. In the figure, C8 is selected from adder high when C4 is 1 and is the AND of the carries of adder low and high when C4 is 0. Adder low can never generate a carry when adder high does not. So either their carry-outs are the same or adder high's carry-out is 1 while adder low's carry-out is 0. By ANDing the two carries, we obtain the correct carry when C4 is 0.
How long does the carry select adder take? Assuming internal carry look-ahead logic is used, the 4-bit adders in Figure 5.15 take four gate delays to compute their sums and three gate delays to compute the stage carry-out. The 2:1 multiplexers add two further gate delays to the path of the high-order sum bits. Thus the 8-bit sum is valid after only six gate delays. This saves one gate delay over the standard two-level carry look-ahead implementation for an 8-bit adder.
5.2.4 TTL Adder and Carry Look-ahead Components
Adders and carry look-ahead components are readily available as standard TTL building blocks.Adders The TTL catalog contains several adder components. Representative of these are the 7482 two-bit binary full adder and the 7483 four-bit binary full adder with fast carry. The schematics are shown in Figure 5.16.
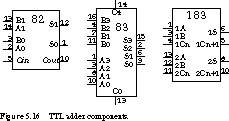
The 7482 contains two cascaded stages of full adder circuits with a ripple carry implemented between the stages. The inputs are two sets of 2 bits to be summed, a carry input, two sum outputs, and a carry-output.
The 7483 is a 4-bit adder and contains the full carry look-ahead logic within the chip. It has two sets of four input bits, four sum bit outputs, a carry-in, and a carry-out. Because of the effectiveness of the carry look-ahead logic, the 4-bit adder is actually faster than the 2-bit adder. The 74183 has two independent single-bit full adders on the same chip.
Carry Look-ahead Units The 74182 is a 4-bit carry look-ahead unit. Its schematic shape is given in Figure 5.17.
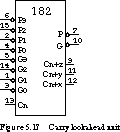
The '182 component has four generate inputs (active low), four propagate inputs (active low), and carry-in (Cn). Its outputs are the three intermediate carries, Cn + x, Cn + y, Cn + z, as well as group P and G (both active low). The latter two outputs make it possible to build multilevel carry look-ahead networks. The '182 component is specially designed to work with the 74181 arithmetic logic unit, to be introduced in the next section.
[Top] [Next] [Prev]
![What is Sarbanes-Oxley[q]](/icons/blank_book.jpg "What is Sarbanes-Oxley[q]"){kind=icon}