2.7 EXAMPLES OF FINITE AUTOMATA CONSTRUCTION

2.6 MINIMIZATION/OPTIMIZATION OF A DFA

Minimization/optimization of a deterministic finite automata refers to detecting those states of a DFA whose presence or absence in a DFA does not affect the language accepted by the automata. Hence, these states can be eliminated from the automata without affecting the language accepted by the automata. Such states are:

• Unreachable States: Unreachable states of a DFA are not reachable from the initial state of DFA on any possible input sequence.

• Dead States: A dead state is a nonfinal state of a DFA whose transitions on every input symbol terminates on itself. For example, q is a dead state if q is in Q F , and ( q , a ) = q for every a in & pound ; .

• Nondistinguishable States: Nondistinguishable states are those states of a DFA for which there exist no distinguishing strings; hence, they cannot be distinguished from one another.

Therefore, optimization entails:

1. Detection of unreachable states and eliminating them from DFA;

2. Identification of nondistinguishable states, and merging them together; and

3. Detecting dead states and eliminating them from the DFA.

2.6.1 Algorithm to Detect Unreachable States

Input M = ( Q , , , q , F )
Output = Set U (which is set of unreachable states)

{Let R be the set of reachable states of DFA. We take two R 's, R _new , and R _old so that we will be able to perform iterations in the process of detecting unreachable states.}

 begin  R   old  =    R   new  = {q   }     while (  R   old  #  R   new  ) do     begin     temp  1  =  R   new     R   old   R   old  =  R   new  temp  2  =   for every  a  in   do     temp  2  = temp  2      (temp  1  ,  a  )  R   new  =  R   new    temp  2  end  U  =  Q     R   new  end 

If p and q are the two states of a DFA, then p and q are said to be ˜ distinguishable states if a distinguishing string w exists that distinguishes p and q .

A string w is a distinguishing string for states p and q if transitions from p on w go to a nonfinal state, whereas transitions from q on w go to a final state, or vice versa.

Therefore, to find nondistinguishable states of a DFA, we must find out whether some distinguishing string w , which distinguishes the states, exists. If no such string exists, then the states are nondistinguishable and can be merged together.

The technique that we use to find nondistinguishable states is the method of successive partitioning. We start with two groups/partitions: one contains all nonfinal states, and other contains all the final state. This is because if every final state is known to be distinguishable from a nonfinal state, then we find transitions from members of a partition on every input symbol. If on a particular input symbol a we find that transitions from some of the members of a partition goes to one place, whereas transitions from other members of a partition go to an other place, then we conclude that the members whose transitions go to one place are distinguishable from members whose transitions goes to another place. Therefore, we divide the partition in two; and we continue this partitioning until we get partitions that cannot be partitioned further. This happens when either a partition contains only one state, or when a partition contains more than one state, but they are not distinguishable from one another. If we get such a partition, we merge all of the states of this partition into a single state. For example, consider the transition diagram in Figure 2.9.

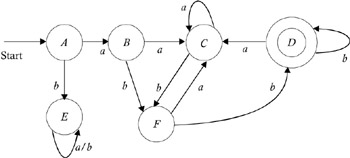
Figure 2.9: Partitioning down to a single state.

Initially, we have two groups, as shown below:

Since

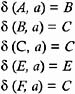
Partitioning of Group I is not possible, because the transitions from all the members of Group I go only to Group I. But since

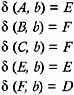
state F is distinguishable from the rest of the members of Group I. Hence, we divide Group I into two groups: one containing A , B , C , E , and the other containing F , as shown below:

Since

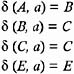
partitioning of Group I is not possible, because the transitions from all the members of Group I go only to Group I. But since

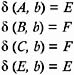
states A and E are distinguishable from states B and C . Hence, we further divide Group I into two groups: one containing A and E , and the other containing B and C , as shown below:

Since

state A is distinguishable from state E . Hence, we divide Group I into two groups: one containing A and the other containing E , as shown below:

Since

partitioning of Group III is not possible, because the transitions from all the members of Group III on a go to group III only. Similarly,

partitioning of Group III is not possible, because the transitions from all the members of Group III on b also only go to Group III.

Hence, B and C are nondistinguishable states; therefore, we merge B and C to form a single state, B ₁ , as shown in Figure 2.10.

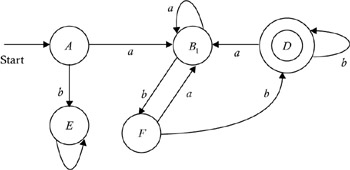
Figure 2.10: Merging nondistinguishable states B and C into a single state B ₁ .

2.6.2 Algorithm for Detection of Dead States

Input M = ( Q , , , q , F)
Output = Set X (which is a set of dead states) {

 {  X  =   for every  q  in (  Q     F  ) do {     flag = true;     for every  a  in   do             if (   (  q  ,  a  ) #  q  ) then                   {                   flag = false                   break                   }     if flag = true then  X  =  X    {q} } }