8.6 Simplification of Boolean Functions
8.6 Simplification of Boolean Functions
Because there is an infinite variety of Boolean functions of n variables , but only a finite number of them are unique, you might wonder if there is some method that will simplify a given Boolean function to produce the optimal form. Of course, you can always use algebraic transformations to attempt to produce this optimal form, but you are not guaranteed to arrive at the best result. On the other hand, there are two methods that will always reduce a given Boolean function to its optimal form: the map method and the prime implicants method. In this book, we will only cover the map method.
Because an optimal form must exist for any logic function, you may wonder why we don't use the optimal form for the canonical form. There are two reasons. First, although it is easy to convert between the truth table forms and the canonical form, it is not as easy to generate the optimal form from a truth table. Second, there may be several optimal forms for a single function.
Using the map method to manually optimize Boolean functions is practical only for functions of two, three, or four variables. With care, you can use it for functions of five or six variables, but the map method is cumbersome to use at that point. For more than six variables, attempting map simplifications by hand would not be wise although it's probably quite reasonable to write a program that uses the map method for seven or more variables.
The first step in using the map method is to build a special two-dimensional truth table for the function (see Figure 8-1). Take a careful look atthese truth tables. They do not use the same forms appearing earlier in this chapter. In particular, the progression of the 2-bit values is 00, 01, 11, 10, not 00, 01, 10, 11. This is very important! If you organize the truth tables in a binary sequence, the mapping optimization method will not work properly. We will call this a truth map to distinguish it from the standard truth table.
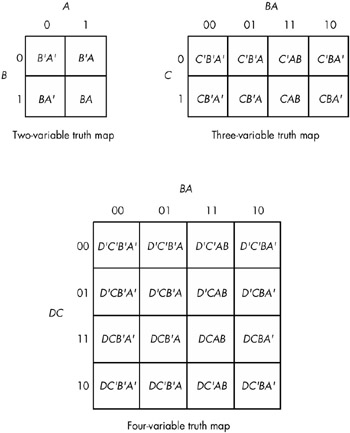
Figure 8-1: Two-, three-, and four-variable truth maps
Assuming your Boolean function is already in sum of minterms canonical form, insert ones for each of the truth map cells corresponding to one of them in terms in the function. Place zeros everywhere else. For example, consider the function of three variables F = C'B'A + C'BA' + C'BA + CB'A' + CB'A + CBA' + CBA . Figure 8-2 shows the truth map for this function.
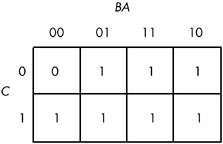
Figure 8-2: A truth map for F = C'B'A + C'BA' + C'BA + CB'A' + CB'A + CBA' + CBA
The next step is to draw outlines around rectangular groups of ones. The rectangles you enclose must have sides whose lengths are powers of two. For functions with three variables, the rectangles can have sides whose lengths are one, two, and four. The set of rectangles you draw must surround all cells containing ones in the truth map. The trick is to draw all possible rectangles unless a rectangle would be completely enclosed within another, but at the same time to draw the fewest number of rectangles. Note that the rectangles may overlap as long as one rectangle does not completely enclose the other. In the truth map in Figure 8-3, there are three such rectangles.
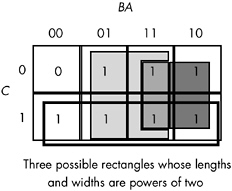
Figure 8-3: Surrounding rectangular groups of ones in a truth map
Each rectangle represents a term in the simplified Boolean function. Therefore, the simplified Boolean function will contain only three terms. You build each term using the process of elimination - eliminate any variables whose primed and unprimed forms both appear within the rectangle. Consider the long skinny rectangle in Figure 8-3 that is sitting in the row where C = 1 . This rectangle contains both A and B in primed and unprimed forms. Therefore, we can eliminate both A and B from the term. Because the rectangle sits in the C = 1 region, this rectangle represents the single literal C .
Now consider the light gray square in Figure 8-3. This rectangle includes C, C', B, B', and A . Therefore, it represents the single term A . Likewise, the dark gray square in Figure 8-3 contains C, C', A, A', and B . Therefore, it represents the single term B .
The final, optimal, function is the sum (logical OR) of the terms represented by the three squares, or F = A + B + C . You do not have to consider the remaining squares containing zeros.
When enclosing groups of ones in the truth map, you must consider the fact that a truth map forms a torus (a doughnut shape). The right edge of the map wraps around to the left edge (and vice versa). Likewise, the top edge wraps around to the bottom edge. This introduces additional possibilities when drawing rectangles around groups of ones in a map. Consider the Boolean function F = C'B'A' + C'BA' + CB'A' + CBA' . Figure 8-4 shows the truth map for this function.
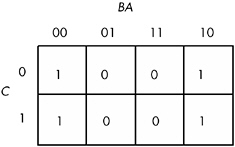
Figure 8-4: Truth map for F = C'B'A' + C'BA' + CB'A + CBA'
At first glance, you would think that the minimum number of rectangles is two, as shown in Figure 8-5.
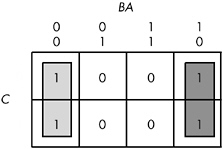
Figure 8-5: First attempt at surrounding rectangles formed by ones
However, because the truth map is a continuous object with the right side and left sides connected, we can actually form a single, square rectangle, as Figure 8-6 shows.
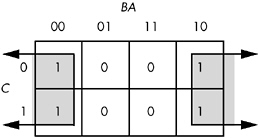
Figure 8-6: Correct rectangle for the function
Why do we care if we have one rectangle or two in the truth map? The answer is that the larger the rectangles are, the more terms they will eliminate. The fewer rectangles that we have, the fewer terms will appear in the final Boolean function.
The example in Figure 8-5 with two rectangles generates a function with two terms. The rectangle on the left eliminates the C variable, leaving A'B' as its term. The rectangle on the right also eliminates the C variable, leaving the term BA' . Therefore, this truth map would produce the equation F = A'B' + A'B . We know this is not optimal (see theorem 13).
Now consider the truth map in Figure 8-6. Here we have a single rectangle, so our Boolean function will only have a single term. Obviously, this is better than an equation with two terms. Because this rectangle includes both C and C', and also B and B' , the only term left is A' . This Boolean function, therefore, reduces to F = A' .
There are only two types of truth maps that the map method cannot handle properly: a truth map that contains all zeros or a truth map that contains all ones. These two cases correspond to the Boolean functions F = 0 and F = 1 (that is, the function number is zero or 2 n ˆ’ 1). When you see either of these truth maps, you will know how to optimally represent the function.
An important thing to remember when optimizing Boolean functions using the mapping method is that you always want to pick the largest rectangles whose sides' lengths are powers of two. You must do this even for overlapping rectangles (unless one rectangle encloses another). Consider the Boolean function F = C'B'A' + C'BA' + CB'A' + C'AB + CBA' + CBA . This produces the truth map appearing in Figure 8-7.
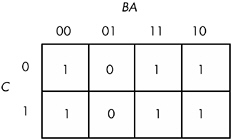
Figure 8-7: Truth map for F = C'B'A' + C'BA' + CB'A' + C'AB + CBA' + CBA
The initial temptation is to create one of the sets of rectangles found in Figure 8-8. However, the correct mapping appears in Figure 8-9.
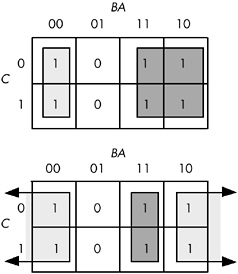
Figure 8-8: Obvious choices for rectangles
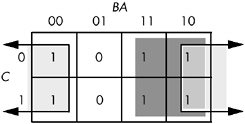
Figure 8-9: Correct set of rectangles for F = C'B'A' + C'BA' + CB'A' + C'AB+CBA'+CBA
All three mappings will produce a Boolean function with two terms. However, the first two will produce the expressions F = B + A'B' and F = AB + A' . The third form produces F = B + A' . Obviously, this last form is the optimized one (see theorems 11 and 12).
For functions of three variables, the size of the rectangle determines the number of terms it represents:
-
A rectangle enclosing a single square represents a minterm. The associated term will have three literals.
-
A rectangle surrounding two squares containing ones represents a term containing two literals.
-
A rectangle surrounding four squares containing ones represents a term containing a single literal.
-
A rectangle surrounding eight squares represents the function F = 1 .
Truth maps you create for functions of four variables are even trickier. This is because there are many places rectangles can hide from you along the edges. Figure 8-10 shows some possible places rectangles can hide.
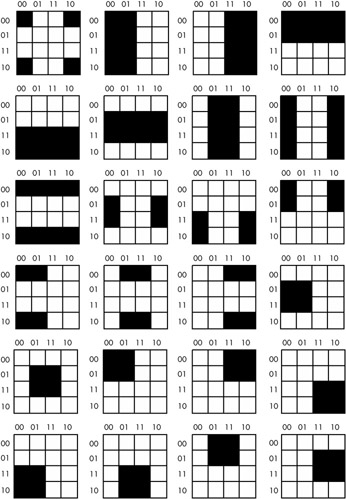
Figure 8-10: Partial pattern list for a 4 —4 truth map
This list of patterns doesn't even begin to cover all of them! For example, the diagrams in Figure 8-10 show none of the 1 —2 rectangles. You must exercise care when working with four variable maps to ensure you select the largest possible rectangles, especially when overlap occurs. This is particularly important when you have a rectangle next to an edge of the truth map.
As with functions of three variables, the size of the rectangle in a four-variable truth map controls the number of terms it represents.
-
A rectangle enclosing a single square represents a minterm. The associated term will have four literals.
-
A rectangle surrounding two squares containing ones represents a term containing three literals.
-
A rectangle surrounding four squares containing ones represents a term containing two literals.
-
A rectangle surrounding eight squares containing ones represents a term containing a single literal.
-
A rectangle surrounding 16 squares represents the function F = 1 .
One final example will demonstrate the optimization of a function containing four variables. The function is F = D'C'B'A' + D'C'B'A + D'C'BA + D'C'BA' + D'CB'A + D'CBA + DCB'A + DCBA + DC'B'A' + DC'BA' , and the truth map appears in Figure 8-11.
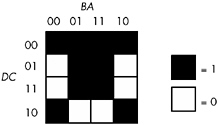
Figure 8-11: Truth map for F = D'C'B'A' + D'C'B'A + D'C'BA + D'C'BA' + D'CB'A + D'CBA + DCB'A + DCBA + DC'B'A' + DC'BA'
Here are two possible sets of maximal rectangles for this function, each producing three terms (see Figure 8-12). Both functions are equivalent; both are optimal (remember, there is no guarantee that there is a unique optimal solution). Either will suffice for our purposes.
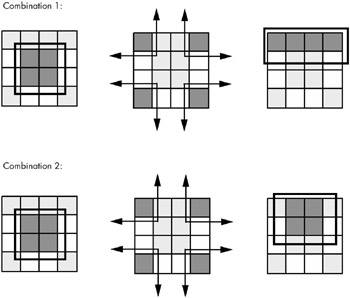
Figure 8-12: Two combinations yielding three terms
First, let's consider the term represented by the rectangle formed by the four corners. This rectangle contains B, B', D , and D', so we can eliminate those terms. The remaining terms contained within these rectangles are C' and A' , so this rectangle represents the term C'A' .
The second rectangle, common to both maps in Figure 8-12, is the rectangle formed by the middle four squares. This rectangle includes the terms A, B, B', C, D , and D' . Eliminating B, B', D, and D' , we obtain CA as the term for this rectangle.
The uppermost of the two combinations in Figure 8-12 has a third term represented by the top row. This term includes the variables A, A', B, B', C' and D' . Because it contains A, A', B, and B' , we can eliminate these terms. This leaves the term C'D' . Therefore, the function represented by the upper truth map is F = C'A' + CA + C'D' .
The lower of the two combinations in Figure 8-12 has a third term represented by the top/middle four squares. This rectangle subsumes the variables A, B, B', C, C', and D' . We can eliminate B, B', C, and C' leaving the term AD . Therefore, the function represented by the lower truth map is F= C'A' + CA + AD' .
EAN: 2147483647
Pages: 144