AGGREGATION-BY-TEMPLATE
|
|
Proposed in Ozsoyoglu, Ozsoyoglu, & Mata (1985, 1987), the aggregation-by-template operator ![]() groups tuples of R1 as follows. Let t be a tuple over attributes (X ∪ Z) such that t[X] = t1[X] for some t1 in R1 and t[Z] = t2[Z] for some tuple t2 in R2.
groups tuples of R1 as follows. Let t be a tuple over attributes (X ∪ Z) such that t[X] = t1[X] for some t1 in R1 and t[Z] = t2[Z] for some tuple t2 in R2.
Each such tuple t defines a group Gt of tuples of R1 such that a tuple v, with v ∊ R1, is in Gt if v[X] = t[X], v[Ya] ∊ t[Za] and v[Yn] ⊆ t[Zn]. Then f is applied to attribute A of tuples in Gt.

The value returned by f applied over an empty group is null. Formally:
Let R1, R2 ∊ A, Y ⊆ Atr (R1), Z = Atr (R2), where | Y | = | Z | ≥ 1, and is defined as:
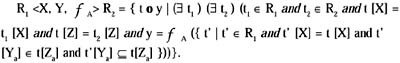
Aggregation-by-template is more convenient than aggregate formation when there are prespecified groupings of attributes for aggregation (common in statistical database applications). Also, aggregation-by-template is based on grouping tuples (i.e., a tuple may belong to more than one group) while aggregate formation is based on partitioning tuples. However, each aggregation operator is expressible by an algebra expression utilizing the other aggregation operator.
|
|
EAN: 2147483647
Pages: 150