RESTRICTION

The restriction operator was proposed in Fortunato et al. (1986) and in Rafanelli & Ricci (1993). In Ozsoyoglu, Ozsoyoglu, & Matos (1987), a similar operator, with the term selection, was proposed and subsequently, the same term was used in Pedersen & Jensen (1999) and in Pedersen, Jensen, & Dyreson (2001). In these papers the authors define the selection operator as a restriction of the set of facts to those that are characterized by valuing a given predicate p on the dimension types evaluated as true. The fact-dimension relations are restricted accordingly, while the dimensions and the schema remain the same (note that the term "dimension" stands for "category attribute," as previously explained).

Recently the term dice was coined and used in Agrawal (1997), Gyssens & Lakshamanan (1997), and Shoshani (1997), especially with regard to OLAP applications. It is an unary operator which selects only the category attribute instances specified by a qualification condition. These instances can be expressed by a complex Boolean expression, where predicates and logical operators (And, Or, Not) appear. The predicate form is <category attribute name> θ <variable | constant>, being θ a logical-mathematical operator of comparison or a set of comparison operators. The fact described by the MAD remains the same, and possible duplicate values are not removed. Possible recomputation of measure instances depends on the summary type of the measure. Therefore, this operation gives, in output, a MAD in which a category attribute of the MAD descriptive space is restricted to the elements of a set, defined as an operand of the operator, together with the name of the MAD. The result of its application is a new MAD defined, based on the same definition schema as the MAD in input.

If the summary type of the measure is count or sum, no problem arises, but if it is, for example, percentage, we have to know if the values in each cell have to be recomputed (i.e., the grand total of the MAD remains 100) or if such values remain the same. In the first case we say that the restriction is normalized. We call this operator N-RESTRICTION and analogously for the summary data "average," where the grand total changes. An example is shown in Figure 15.

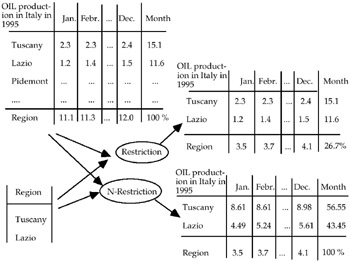
Figure 15

Therefore, given a (simple) MAD s₁, let us suppose the summarizability conditions have been verified. Let be the six-tuple which defines s₁, where is formed by e₁ and i₁, respectively its explicit and implicit category attributes. Let be a category attribute chosen among the category attributes A_B1j of the base relation of s₁ (with j = 1, …, k, being k the cardinality of s₁, i referring to the ith fact described by s₁ and with x ∊ {1, …, k}).

The restriction of s₁ by A_1x is a new MAD s'₁ defined on the same descriptive space schema, but with the category attribute with the same name of A_1x having as definition domain a subset of the original one, i.e., formed by the instances of A_1x. Then, given and a₁ a subset of E_t, with t ∊ k and E_t ⊂ e₁ = { E₁, E₂, …, E_M}, i.e., the set of its explicit category attributes of s₁, the restriction of new MAD s'₁ is defined by the six-tuple where .

Notice that we can generalize the operator considering, instead a₁, all the set of category attributes A_B1j and, for each attribute, a subset of its definition domain. The operator defined above will be applied iteratively to the first, the second, …, the k-th attribute.

The eventual recomputation of the summary value of the MAD depends on the summary type of the MAD as well as on the type of restriction (no recomputation if it is a regular restriction, eventual recomputation if it is a normalized restriction).