19.1 Arithmetic with Polynomials

Team-Fly

---

19.1 Arithmetic with Polynomials

We start by looking at arithmetic in the field , the finite field with 2ⁿ elements, where an element of is represented as a polynomial f(x) = a_n−1xⁿ⁻¹ + a_n−2xⁿ⁻² + ··· + a₁x + a₀ with coefficients a_i in (which is isomorphic to ). Equivalently, an element of can be represented simply as an n-tuple of polynomial coefficients, each representation offering its own advantages. The polynomial representation is well suited for manual calculation, while the representation as a tuple of coefficients corresponds well to a computer's binary representation of numbers. To demonstrate this, we notate as a sequence of eight polynomials and again as eight 3-tuples with their associated numerical values (see Table 19.1).

Table 19.1: Elements of

Polynomials in	3-Tuples in			Numerical value
0	0	0	0	'00'
1	0	0	1	'01'
x	0	1	0	'02'
x + 1	0	1	1	'03'
x2	1	0	0	'04'
x2 + 1	1	0	1	'05'
x2 + x	1	1	0	'06'
x2 + x + 1	1	1	1	'07'

Addition of polynomials proceeds by adding the coefficients in : If f(x) := x² + x and g(x) := x² + x + 1, then f(x) + g(x) = 2x² + 2x + 1 = 1, since 1 + 1 = 0 in . We can carry out addition of 3-tuples in column by column. We see, then, for example, that the sum of (1 1 0) and (1 1 1) is (0 0 1):

The addition of digits takes place in and is not to be confused with binary addition, which can involve a carry. This process is reminiscent of our XOR function in Section 7.2, which executes the same operation in for large n.

Multiplication in is accomplished by multiplying each term of the first polynomial by each term of the second and then summing the partial products. The sum is then reduced by an irreducible polynomial of degree 3 (in our example modulo m(x) := x³ + x + 1):^[3]

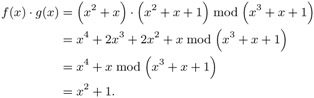
This corresponds to the product of 3-tuples (1 1 0) • (1 1 1) = (1 0 1), or, expressed in hexadecimal notation, '06' • '07' = '05'.

The abelian group laws hold in with respect to addition and in \ {0} with respect to multiplication (cf. Chapter 5). The distributive law holds as well.

The structure and arithmetic of can be carried over directly to the field , which is the field that is actually of interest in studying Rijndael. Addition and multiplication are carried out as in our above example, the only differences being that has 256 elements and that an irreducible polynomial of degree 8 will be used for reduction. For Rijndael this polynomial is m(x) := x⁸ + x⁴ + x³ + x + 1, which in tuple representation is (1 0 0 0 1 1 0 1 1), corresponding to the hexadecimal number '011B'.

Multiplication of a polynomial

by x (corresponding to a multiplication • '02') is particularly simple:

where the reduction modulo m(x) is required only in the case a₇ ≠ 0, and then it can be carried out by subtracting m(x), that is, by a simple XOR of the coefficients.

For programming one therefore regards the coefficients of a polynomial as binary digits of integers and executes a multiplication by x by a left shift of one bit, followed by, if a₇ = 1, a reduction by an XOR operation with the eight least-significant digits '1B' of the number '011B' corresponding to m(x) (whereby a₇ is simply "forgotten"). The operation a • '02' for a polynomial f, or its numerical value a, is denoted by Daemen and Rijmen by b = xtime(a). Multiplication by powers of x can be executed by successive applications of xtime.

For example, multiplication of f(x) by x + 1 (or '03') is carried out by shifting the binary digits of the numerical value a of f one place to the left and XOR-ing the result with a. Reduction modulo m(x) proceeds exactly as with xtime. Two lines of C code demonstrate the procedure:

   f ^= f << 1;    /* multiplication of f by (x + 1) */   if (f & 0×100) f ^= 0×11B;    /* reduction modulo m(x) */ 

Multiplication of two polynomials f and h in can be speeded up by using logarithms: Let g(x) be a generating polynomial^[4] of \ {0}. Then there exist m and n such that f ≡ g^m and h ≡ gⁿ. Thus f · h ≡ g^m+n mod m(x).

From a programming point of view this can be transposed with the help of two tables, into one of which we place the 255 powers of the generator polynomial g(x) := x + 1 and into the other the logarithms to the base g(x) (see Tables 19.2 and 19.3). The product f · h is now determined by three accesses to these tables: From the logarithm table are taken values m and n for which g^m = f and gⁿ = h. From the table of powers the value g^{((n+m)mod255)} is taken (note that g^ord(g) = 1).

With the help of this mechanism we can also carry out polynomial division in . That is,

Table 19.2: Powers of g(x) = x + 1

1	3	5	15	17	51	85	255	26	46	114	150	161	248	19	53
95	225	56	72	216	115	149	164	247	2	6	10	30	34	102	170
229	52	92	228	55	89	235	38	106	190	217	112	144	171	230	49
83	245	4	12	20	60	68	204	79	209	104	184	211	110	178	205
76	212	103	169	224	59	77	215	98	166	241	8	24	40	120	136
131	158	185	208	107	189	220	127	129	152	179	206	73	219	118	154
181	196	87	249	16	48	80	240	11	29	39	105	187	214	97	163
254	25	43	125	135	146	173	236	47	113	147	174	233	32	96	160
251	22	58	78	210	109	183	194	93	231	50	86	250	21	63	65
195	94	226	61	71	201	64	192	91	237	44	116	156	191	218	117
159	186	213	100	172	239	42	126	130	157	188	223	122	142	137	128
155	182	193	88	232	35	101	175	234	37	111	177	200	67	197	84
252	31	33	99	165	244	7	9	27	45	119	153	176	203	70	202
69	207	74	222	121	139	134	145	168	227	62	66	198	81	243	14
18	54	90	238	41	123	141	140	143	138	133	148	167	242	13	23
57	75	221	124	132	151	162	253	28	36	108	180	199	82	246	1

Table 19.3: Logarithms to base g(x) = x + 1 (e.g., log_g(x) 3 = 25, log_g(x) 255 = 7)

	0	25	1	50	2	26	198	75	199	27	104	51	238	223	3
100	4	224	14	52	141	129	239	76	113	8	200	248	105	28	193
125	194	29	181	249	185	39	106	77	228	166	114	154	201	9	120
101	47	138	5	33	15	225	36	18	240	130	69	53	147	218	142
150	143	219	189	54	208	206	148	19	92	210	241	64	70	131	56
102	221	253	48	191	6	139	98	179	37	226	152	34	136	145	16
126	110	72	195	163	182	30	66	58	107	40	84	250	133	61	186
43	121	10	21	155	159	94	202	78	212	172	229	243	115	167	87
175	88	168	80	244	234	214	116	79	174	233	213	231	230	173	232
44	215	117	122	235	22	11	245	89	203	95	176	156	169	81	160
127	12	246	111	23	196	73	236	216	67	31	45	164	118	123	183
204	187	62	90	251	96	177	134	59	82	161	108	170	85	41	157
151	178	135	144	97	190	220	252	188	149	207	205	55	63	91	209
83	57	132	60	65	162	109	71	20	42	158	93	86	242	211	171
68	17	146	217	35	32	46	137	180	124	184	38	119	153	227	165
103	74	237	222	197	49	254	24	13	99	140	128	192	247	112	7

We now ratchet the complexity level up one notch and consider arithmetic with polynomials of the form f(x) = f₃x³ + f₂x² + f₁x + f₀ with coefficients f_i in , that is, coefficients that are themselves polynomials. The coefficients of such polynomials can be represented as fields of four bytes each. Now things begin to get interesting: While addition of such polynomials f(x) and g(x) again takes place by means of a bitwise XOR of the coefficients, the product h(x) = f(x)g(x) is calculated to be

with coefficients h_k := f_i • g_j, where the summation sign indicates addition ⊕ in .

After reduction of h(x) by a polynomial of degree 4, one again obtains a polynomial of degree 3 over .

For this Rijndael uses the polynomial M(x) := x⁴ + 1. Usefully, x^j mod M(x) = x^jmod4, so that h(x) mod M(x) can be easily computed as

with

From this one concludes that the coefficients d_i can be computed by matrix multiplication over :

It is precisely this operation with the constant, invertible modulo M(x), polynomial a(x) := a₃x³ + a₂x² + a₁x + a₀ over , with coefficients a₀(x) = x, a₁(x) = 1, a₂(x) = 1, and a₃(x) = x + 1, that is executed in the so-called MixColumn transformation, which constitutes a principal component of the round transformations of Rijndael.

^[3]A polynomial is said to be irreducible if it divisible (without remainder) only by itself and 1.

^[4]g generates \ {0} if g has order 255. That is, is the powers of g run through all the elements of \ {0}.

---

Team-Fly