Chapter 1: The Vasicek Model
The initial formulation of Vasicek's model is very general, with the short- term interest rate being described by a diffusion process. An arbitrage argument, similar to that used to derive the Black-Scholes option pricing formula [ 8 ], is applied within this broad framework to determine the partial differential equation satisfied by any contingent claim. A stochastic representation of the bond price results from the solution to this equation. Vasicek then allows more restrictive assumptions to formulate the specific model with which his name is associated.
The consistency of the model specifications with an underlying economic equilibrium is not proved. Rather, it is implicitly assumed. The special case of the general model formulation, which Vasicek uses for illustrative purposes, was suggested by Merton [ 40 ] in a study of price dynamics in a continuous time, equilibrium economy. Equilibrium conditions imply that interest rates are such that the demand and supply of capital are equally matched.
1.1 Preliminaries
First, define the following variables :
| P ( t, T ) | - | time t price of a discount bond maturing at time T , t ‰ T , with P ( T , T )=1. |
| R ( t , ) | - | time t rate of interest applicable for period . Intermsof the return on a discount bond, this rate is defined as the internal rate of return, at time t , on a bond with maturity date T = t + . |
| r ( t ) | - | instantaneous rate of interest (short rate) at time t . |
| f ( t , T ) | - | instantaneous forward interest rate i.e. time t assessment of the instantaneous rate of interest applicable at time T . |
The following relationships apply:
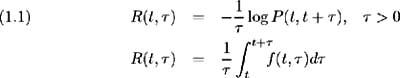
or explicitly for the forward rate:
The short rate is defined as the instantaneous rate of interest at time t :
Vasicek makes the following three assumptions:
| |
The current short interest rate is known with certainty . However, subsequent values of the short rate are not known. The assumption is made that r ( t ) follows a stochastic process. Also assume that r ( t ):
-
is a continuous function of time,
-
follows a Markovian process. That is, given its current value, future developments of the short rate are independent of past movements.
This implies that the short rate process is fully characterised by a single state variable, i.e. its current value, and the probability distribution of r ( t *), t * ‰ t is fully determined by r ( t ). A continuous Markovian process is called a diffusion process, which is described by the stochastic differential equation:
where v ( r , t ) is the instantaneous drift and s 2 ( r , t ) the instantaneous variance of r ( t ). z ( t ) is a Wiener process under a given measure Q .
| |
| |
The time t price of a discount bond with maturity T , P ( t , T ), is fully determined by the time t assessment of { r ( t *), t ‰ t * ‰ T }, the segment of the short rate over the remaining term of the bond. Moreover, the development of the short rate over [ t , T ] is fully determined by its current value r ( t ), so the bond price may be written as a function of the current short rate:
Hence the entire term structure is determined by the short rate.
| |
| |
The market is assumed to be efficient. This implies:
-
there are no transaction costs;
-
information is simultaneously distributed to all investors;
-
investors are rational with homogeneous expectations;
-
profitable, riskless arbitrage is not possible.
| |
EAN: 2147483647
Pages: 132