11.9 Markovian HJM model
11.9 Markovian HJM model
In term structure models such as the Vasicek [ 50 ] and CIR [ 18 ] models, the starting point is the dynamics of the short-term interest rate. The drift and volatility are specified such that the short-term interest rate is Markovian. In the HJM framework the forward rate volatility and initial forward rate curve are used to characterise the term structure. Such a specification may give rise to non-Markovian short-term interest rate dynamics. In fact many HJM-based models cannot occur in a framework of Markovian short-term interest rates. The Markovian property of the short-term interest rate is desirable since it allows for simpler numerical valuation procedures of the term structure and interest rate contingent claims since:
-
The term structure at time t is a function of t , maturity T and the time t short-term interest rate.
-
The evolution of the short-term interest rate may be modelled using a recombining tree or lattice, which has significant implications for computational efficiency.
Carverhill [ 14 ] andJeffrey[ 32 ] characterise restrictions on the volatility structure of forward rates that lead to Markovian short-term interest rate dynamics.
11.9.1 Deterministic bond price volatility.
Carverhill requires the bond price volatility structure to be deterministic, that is a i ( t, T )= ˆ’ ˆ« T t ƒ i ( t, v ) dv, i = 1, , n are functions of t and T only. Also each a i ( t, T ) is assumed to be twice continuously differentiable with respect to the maturity time T .
Consider (11.33), the short-term interest rate process within the HJM framework:
Taking the derivative with respect to t , the dynamics of the short-term interest rate may be found as:
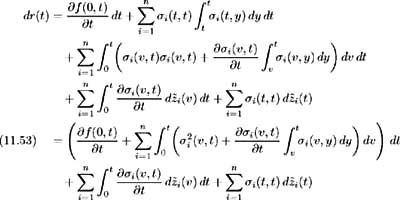
Carverhill [ 14 ] gives the following necessary and sufficient condition for the above short-term interest rate specification to be Markovian:
Assuming ƒ i ( t, T ) ‰ 0, T ˆˆ [0, ], t ˆˆ [0, T ], i = 1, , n , then there exist functions g i ( ·) and h i ( ·) such that:
The HL model, as examined in §11.7, satisfies the above condition. It corresponds to a forward rate volatility ƒ ( t, T )= ƒ ,where ƒ is a strictly positive constant. The short-term interest rate is defined in (11.39) and leads to short-term interest rate dynamics of the form [23] :
The disadvantage , of the HL model, that only parallel shifts in the term structure are possible, is clearly demonstrated by the short-term interest rate dynamics. We expect shorter maturity forward rates to be more volatile than longer maturity forward rates. Hence, in an attempt to obtain more realistic term structure dynamics, let the forward rate volatility be a decreasing function of time, more specifically , allow for an exponentially dampened volatility structure: ƒ ( t, T )= ƒ e ˆ’³ ( T ˆ’ t ) where ³ , ƒ > 0 are constants. Making use of (11.32) the corresponding forward rate process is:
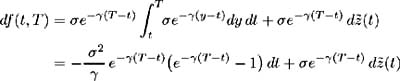
From (11.52) the short-term interest rate is expressed as:
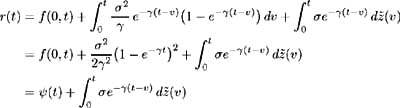
where ˆ ( t ) = f (0, t ) + ![]() (1 ˆ’ e ˆ’³ t ) 2 .
(1 ˆ’ e ˆ’³ t ) 2 .
Now, using (11.53), the short-term interest rate dynamics are specified as:

This is an extension of the constant parameter Vasicek model studied in Chapter 1. Here the mean reversion level ˆ ² ( t )/ ³ + ˆ ( t ), is a function of time, but the speed of mean reversion ³ , and volatility ƒ , are constant. The Hull-White extension of the Vasicek model (see (7.4) Chapter 7) allows for time-dependent reversion level, reversion speed and volatility. However, Hull- White observe that allowing all three parameters to be time-dependent leads to unreasonable evolution of the volatility structure and hence they recommend a model where reversion speed and volatility are kept constant. It appears that the formulation of the Vasicek model within the HJM framework results in an optimal extension of the model.
11.9.2 More general framework.
Jeffrey [ 32 ] develops a more general result, allowing a stochastic volatility structure. However, he restricts the volatility to be a function of valuation time t , maturity time T and the time t short-term interest rate r ( t ) only. Consequently, within a one-factor framework ( n = 1) the HJM forward rate volatility may be expressed as ƒ ( ‰ , t, T ) ‰ ƒ ( r, t, T ). Notice that ƒ ( r, t, t ) is the volatility of the short-term interest rate, as shown in (11.53).
In this analysis, the requirement that the term structure be a function of t , T and the Markovian short-term interest rate r ( t ) leads to restrictions on the form of the forward rate volatility structure and the initial forward rate curve. These restrictions take the form of necessary and sufficient conditions indicating:
-
which HJM models exhibit Markovian characteristics, and
-
what volatility and initial term structure restrictions are inherent in models within a Markovian setting.
Jeffrey shows that a forward rate volatility ƒ ( r, t, T ), leads to a Markovian short-term interest rate if there exist functions ( r, t ) and h ( t, T ) such that:
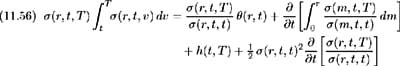
To illustrate this condition, consider a constant forward rate volatility structure, that is ƒ ( r, t, T )= ƒ . By (11.56) we must find a ( r, t ) and h ( t, T )such that:
A simple choice of h ( t, T )= ƒ 2 T gives ( r, t )= ˆ’ƒ 2 t and the required condition is satisfied. Hence the associated short-term interest rate is Markovian. Now, consider a forward rate volatility structure ƒ ( r, t, T )= ƒ r ² for some ² > 0. Evaluating (11.56), we require
which is impossible , since there is no choice of h ( t, T ) such that the right-hand side is independent of T . We may conclude that this forward rate structure is not admissible in a Markovian short-term interest rate paradigm.
Further to the above condition, Jeffrey formulates a requirement on the structure of the initial forward rate curve. Given a forward rate volatility structure satisfying (11.56), the associated initial forward rate curve must have the form:
where k ( T ) = ˆ’ ˆ« T h ( s, T ) ds for any h ( t, T ) that is valid for (11.56) to hold. Since the set of allowable initial forward rate curves is determined by the choice of h ( t, T ) in (11.56), Jeffrey presents a result [ 32 , Theorem 1] detailing the restrictions on the initial forward rate term structure.
We have ƒ ( r, t, T ), a volatility structure satisfying (11.56) and let ¾ ( t, T )be a deterministic function of t and T . Then one of the following is true:
-
If ƒ ( r, t, T ) is not of the form ¾ ( t, T ) ƒ ( r, t, t ), then there is only one pair of functions ( r, t ) and h ( t, T ) such that (11.56) holds. Here k ( T ) and the allowable initial forward rate curve and completely defined by ƒ ( r, t, T ).
-
If ƒ ( r, t, T ) is of the form ¾ ( t, T ) ƒ ( r, t, t ), then the set of valid pairs of functions ( r, t ) and h ( t, T ) satisfying (11.56) may be represented as:

where h p ( t, T ) is any particular h ( t, T ) satisfying (11.56) and c ( t )is any function of time t . The choice of c ( t ) is such that any function k ( T ) (and hence any initial forward rate curve) may be fitted in (11.57).
This result clearly demonstrates that the volatility structure and initial forward rate curve cannot be fitted independently. If the volatility structure is not of the form ¾ ( t, T ) ƒ ( r, t, t ), then it uniquely determines the allowable initial forward rate curve. If the volatility structure is of the form ¾ ( t, T ) ƒ ( r, t, t ), then k ( T ) may be chosen to fit any initial forward rate curve.
Consider the short-term interest rate model proposed by CIR [ 18 ] as studied in Chapter 2. The short-term interest rate process has the form (see equation (2.17) Chapter 2):
Since the short-term interest rate volatility ƒ ( r, t, t )= ƒ ˆ r , is not purely deterministic, and it is reasonable that the associated forward rate volatility maintains this stochastic characteristic, it is not allowable within the analysis outlined by Carverhill. However, we show that the forward rate volatility associated with the CIR short-term interest rate process does in fact satisfy the criteria for a Markovian short-term interest rate, as set out by Jeffrey. Consider the analysis of the CIR model within the HJM framework in §11.8. The forward rate process is derived in (11.49) as:
and so the forward rate volatility ƒ ( r, t, T ) may be found as:
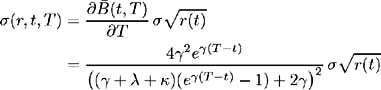
Since ƒ ( r, t, T ) is of the form ¾ ( t, T ) ƒ ( r, t, t ), with
we conclude that the short-term interest rate within the CIR model is Markovian and that any initial forward rate curve may be fitted [24] .
[23] The short-term interest rate dynamics may be determined using (11.53) with n =1 and ƒ ( t, T )= ƒ .
[24] The admissible initial forward rate curve will be subjected to the requirement that 2 ( t ) ‰ ƒ 2 , as explained in §11.8. However, this restriction is required to prevent negative interest rates and is not associated with the Markovian nature of the short-term interest rate process.
EAN: 2147483647
Pages: 132
- An Emerging Strategy for E-Business IT Governance
- Linking the IT Balanced Scorecard to the Business Objectives at a Major Canadian Financial Group
- Measuring and Managing E-Business Initiatives Through the Balanced Scorecard
- Measuring ROI in E-Commerce Applications: Analysis to Action
- Managing IT Functions