8.5 A fundamental flaw
8.5 A fundamental flaw
Let us revisit the calibration methodology outlined in §8.3. It is easy to see that this methodology contains a fundamental flaw. No distinction is made between the current term structure of interest rate volatilities and future volatilities of the short- term interest rate. Equation (8.5) shows that the standard deviation of the time t = 1 short-term interest rate is matched to the volatility of the 2-year yield, and hence the volatility of the short-term interest rate at time t = 1 is matched to the current volatility of the 2-year yield. Assuming time steps of 1 year, this may be generalised as follows : the time t = t * volatility of the short-term interest rate is equated to the current (time t = 0) volatility of the ( t * + 1)-year yield. Surprisingly, there are few texts that make mention of this flaw.
The artificial link between the future short-term interest rate volatilities and the term structure of volatilities is often cited as a major drawback of the BDT model. In fact Rebonato [ 45 ] discusses the fact that "the term structure of volatilities is completely determined by the specification of the future volatility of the short rate" and examines the shape of the term structure of volatilities for various functional forms of the short-term interest rate volatility. However, he does not explicitly show the relationship between the volatility term structure and the short-term interest rate volatility function, nor does he explicitly discuss the calibration to market- observed volatilities thereby side-stepping the issue.
A slightly more complex procedure to that outlined in §8.3 is required to build a binomial tree representing both the observed interest rate and volatility term structures. The following methodology [ 15 ] allows matching of the observed interest rate and volatility term structures.
8.5.1 Preliminaries.
We begin with the observed interest rate and volatility term structures represented by: P ( i ) as the price of a discount bond [7] maturing at time i ” t and ƒ R ( i ) as the volatility of the yield on this bond. Let
| ” t | - | time step size chosen for the tree, |
| u ( i ) | - | median short-term interest rate at time i ” t , |
| ƒ ( i ) | - | volatility of the short-term interest rate at time i ” t , |
| r i,j | - | short-term interest rate at time i ” t node j , applicable for the period [ i ” t, ( i +1) ” t ], |
| d i,j | - | the time i ” t , state j value of a discount bond maturing at time ( i +1) ” t , hence: d i,j =1 / (1 + r i,j ” t ). In [ 15 ] this is called the one-period discount factor at node ( i, j ). |
| Q i,j | - | time 0 value of a security paying: |
| 1 if node( i, j ) is reached, | ||
| 0 otherwise . |
The Q i,j s are in fact Arrow-Debreu securities. For a discussion on this topic see [ 45 ]. They may be viewed as discounted probabilities; hence, by definition Q 0,0 = 1.
Hence, the current (time t = 0) price of a discount bond maturing at time ( i + 1) ” t may be expressed as:
for j ˆˆ ![]() , where
, where ![]() is the set of all possible states at time i . The calibration of the tree is by forward induction, where the time i ” t Arrow-Debreu securities are updated using the already known Arrow-Debreu securities at time ( i ˆ’ 1) ” t as follows:
is the set of all possible states at time i . The calibration of the tree is by forward induction, where the time i ” t Arrow-Debreu securities are updated using the already known Arrow-Debreu securities at time ( i ˆ’ 1) ” t as follows:
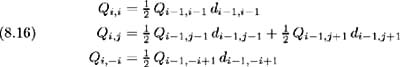
8.5.2 Fitting the interest rate and volatility term structures.
From (8.7) the short-term interest rate at each node ( i, j ) may be represented as:
First we define the notation used to index the nodes of the tree. At starting time i = 0, there is a single state j = 0. At each subsequent time i there are ( i + 1) possible states indexed as j = ˆ’ i, ˆ’ i +2, , i ˆ’ 2, i . The state index represents the net moves required to reach it. For example, at time i = 4, there are 5 possible states with indices { ˆ’ 4; ˆ’ 2; 0; 2; 4} corresponding to 4 down moves, 1 up and 3 down moves (net 2 down moves), 2 up and 2 down moves (net zero move), 3 up and 1 down move (net 2 up moves) and 4 up moves respectively.
Now from the initial node (0, 0) at the root of the tree, we have a possible up move and possible down move. Hence node (1, 1) is denoted U and node (1, ˆ’ 1) is denoted D . At these nodes define the following:
| P i U , P i D | - | price, at nodes U and D respectively, of discount bond with maturity i ” t after an initial up or down move, i ‰ 1, |
| R i U , R i D | - | the discount bond yields at nodes U and D respectively, corresponding to the above discount bond prices, |
These values of P U ( i ) and P D ( i ) must be consistent with the observed values of P ( i ) and ƒ R ( i ). Therefore the following relationships must hold:
Equations (8.18) may be solved simultaneously for P U ( i ) and P D ( i ) as:
and
where (8.19) must be solved numerically for P D ( i ).
As in §8.5.1 we define state prices, this time corresponding to nodes U and D , as follows:
| Q U,i,j | - | value at node U of security paying 1 if node ( i, j ) is reached, 0 otherwise, |
| Q D,i,j | - | value at node D of security paying 1 if node ( i, j ) is reached, 0 otherwise. |
By definition Q U ,1,1 = 1 and Q U, 1, ˆ’ 1 = 1 and so from (8.15) the values at nodes U and D of a discount bond maturing at time ( i +1) ” t may be written as [8] :
respectively.
The state prices may then be updated as in (8.16):
and
8.5.3 Basic algorithm.
First, set the initial values:
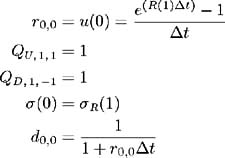
Now for each i = 1, , N ˆ’ 1
-
Using a numerical method such as Newton-Raphson solve (8.19) for P D ( i + 1) and then solve for P U ( i + 1) by means of (8.20).
-
Now making use of P D ( i + 1) and P U ( i + 1) derived above, equations (8.21) and (8.22) may be used to solve for ƒ ( i ) and u ( i ). The following substitution is made:
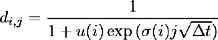
Hence:
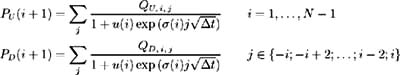
and ƒ ( i ) and u ( i ) may be found using a two dimensional Newton- Raphson (or other optimisation ) technique.
-
Using these calculated values of ƒ ( i ) and u ( i ) the one period short-term interest rates and discount factors may be found for each node j = ˆ’ i , , i using (8.17) and the definition of the discount factor as d i,j = 1/(1 + r i,j ” t ).
-
Q U,i,j and Q D,i,j may now be updated using equations (8.23).
The fundamental concept behind this calibration methodology is rather simple. The observed term structure of volatilities represents the volatilities of current rates of various maturities. A shift up and shift down of the entire term structure is simulated by the U and D nodes. The magnitude of this up and down shift is determined by the bond yield volatility (as represented by (8.18b)). This allows the volatility term structure information to be incorporated. Comparing this to the original BDT calibration methodology in §8.3 highlights their error of matching the initial time volatility of the i -year interest rate to the short-term interest rate volatility at year ( i ˆ’ 1). Their methodology could be used to build a tree representing the interest rate term structure and future volatilities of the short-term interest rate. Obviously this is only possible if one has a view of short-term interest rate volatilities at each time interval in the future.
[7] This discount bond price is related to yield R ( i ) by:
[8] Here N is the total number of time steps in the tree.
EAN: 2147483647
Pages: 132