2.10 Extending the model to allow time-dependent drift
2.10 Extending the model to allow time-dependent drift
Consider extending the model specification to allow for a time-dependent drift parameter. Hence the short- term interest rate dynamics become:
Due to the Markovian nature of the model, we assume that all information about past movements and expectations of future movements is contained in the current ( observed ) term structure. Therefore the functional form of the time-dependent parameter ( t ), may be determined from observed bond prices and the values of the constant parameters. No prior restrictions are placed on the functional form of ( t ) since it is determined so as to reflect the specific observed term structure.
Consider the conditional expectation of r ( s ) with the time-dependent parameter ( t ). Following the methodology of §(2.7.1) we have the integral form of the short-term interest rate process:
Taking expectations and differentiating with respect to s produces:
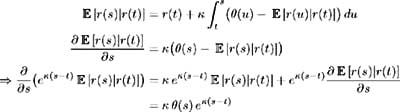
so, integrating over [ t, s ] gives the conditional expectation of r ( s )as:
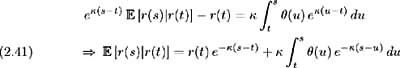
The bond price takes the same functional form as specified in (2.27), with a modification to one of the parameters as depicted below:
where:
Given this formulation of the bond price and the observed term structure, (2.44) can be solved for ( s ) for all s ˆˆ [ t, T ] which could then be used in conjunction with (2.41) to determine future expectations of the short-term interest rate as specified by the current observed term structure.
EAN: 2147483647
Pages: 132