15.4 Principal Component Analysis
15.4 Principal Component Analysis
Principal component analysis (PCA) may be performed on a time series of historical term structure data in an attempt to identify the dominant factors driving its evolution. PCA produces factors maximising successive contributions to overall variance. Hence these factors attempt to explain the diagonal of the covariance matrix. The resulting factors are surrogate volatility factors derived from an empirical analysis of term structure data.
Principal component analysis provides a direct indication of the number and general shape of factors driving the term structure movements. A historical estimate of the magnitude of the volatility functions is also obtained as part of the analysis. These driving factors are both econometrically and financially justifiable, but like all historical calibration methodologies, will not exactly recover market prices of traded derivative instruments.
Many analyses have used spot interest rates as a description of the term structure; here we consider a finite set of forward rates of predetermined tenor, that span the whole term structure. Within the HJM framework each instantaneous forward rate is a stochastic variable in its own right, displaying some degree of correlation with other forward rates. To model a realistic evolution of the term structure one needs to determine a set of forward rate variances (volatilities) as well as covariances ( correlations ) between the forward rates.
15.4.1 Methodology of principal component analysis
On each day t we observe a vector f ( t ), of N forward rates with maturities t + j , j = 1, , N , that is f ( t )=[ f ( t, t + 1) f ( t, t + 2) f ( t, t + N )] ² . A discrete time representation of the forward rate evolution depicted in equation (15.2) is:
Since we have N different forward rates, we may have at most N sources of uncertainty.
15.4.1.1 Volatility Component
Choice of two volatility functions is possible:
-
Gaussian volatility function, where
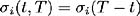
is a deterministic function of term to maturity T ˆ’ t , ˆ i =1, , N .
-
Lognormal volatility function, that is
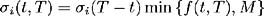
where ƒ i ( T ˆ’ t ) is a deterministic function of term to maturity T ˆ’ t , ˆ i =1, , N , and M is some large positive constant [2] .
15.4.1.2 Drift component
The drift vector in (15.7), ± = [ ± ( t , t + 1) ± ( t , t + 2) ± ( t , t + N )] can be determined from the historical data. For purposes of pricing contingent claims, we derive the drift from the no arbitrage condition such that it is consistent with the risk-neutral valuation framework. This implies that for purposes of determining the covariance matrix, we may assume ± = 0. Alternatively, mean adjusted changes in forward rates may be used, thereby isolating the unexpected changes in forward rates [3] . Since PCA deals with unexpected changes in the term structure, the drift does not enter the calculations and the components obtained from the two methodologies are consistent.
15.4.1.3 Calculation Methodology
From (15.7), we define the ( N — 1) vector d ( t )=[ d 1 ( t ) d 2 ( t ) d N ( t )] ² where each element is constructed as:
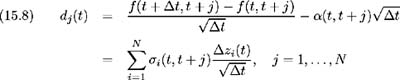
where ![]() , are standard normal. d j ( t ) is the mean-adjusted change in forward rate with maturity t + j over time period [ t, t + ” t ] and represents a realisation of the random variable d j , the change in the j maturity forward rate over some time period ” t .
, are standard normal. d j ( t ) is the mean-adjusted change in forward rate with maturity t + j over time period [ t, t + ” t ] and represents a realisation of the random variable d j , the change in the j maturity forward rate over some time period ” t .
For a set of historical time-series data with K observations of vector d ( t k ), k = 1, , K we define [4] :
where D is a ( N — K ) matrix with columns d ( t k ), k = 1, , K and & pound ; is the ( N — N ) covariance matrix with elements [5] i,j = covar( d i ,d j ). Since this covariance matrix is symmetrical and positive semi-definite, we can find an orthogonal [6] matrix A such that:
where is an ( N — N ) diagonal matrix with elements » m , m = 1, , N such that » 1 ‰ » 2 ‰ ‰ » N . The columns of the ( N — N ) matrix A = [ a 1 , a 2 , , a N ] are the N eigenvectors of covariance matrix , while the N diagonal elements matrix are the corresponding eigenvalues.
15.4.2 Interpretation of the Principal Components
Let us examine what we have achieved by the above transformation. The starting point is an ( N — K ) matrix D = [ d ( t 1 ), d ( t 2 ), , d ( t K )], its columns being K observations the original vector of variables d ( ·)=[ d 1 ( ·) d 2 ( ·) d N ( ·)] ² . Multiplication by the transpose of the orthogonal matrix A transforms D into a new matrix G :
where G = [ g ( t 1 ), g ( t 2 ), , g ( t K )] is an ( N — K ) matrix with columns being realisations of the vector of new variables g ( ·)=[ g 1 ( ·) g 2 ( ·) g N ( ·)] ² . We have defined the new variables as the weighted sums of the original variables, the weights being the elements of the corresponding eigenvectors. Hence the new variable g i is the weighted sum of all original variables d j , j = 1, , N , weighted by the elements of the i th eigenvector a i :
Making use of (15.9), (15.10) and (15.11) the definition of G , we find:
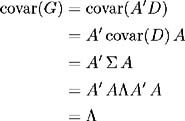
Therefore the diagonal matrix of eigenvalues , is the covariance matrix of the new variables. Since the transformed variables have zero covariance, they are orthogonal (statistically independent). Originally, the stochastic evolution of each forward rate is driven by a separate source of uncertainty which has some degree of correlation with all other sources of uncertainty driving other points on the yield curve. We have transformed to a set of factors, each affecting every point on the yield curve, the extent to which each forward rate is affected is determined by the eigenvector. By virtue of matrix A 's orthogonality we have:
and so each original variable d j , j = 1, , N may be written as:
A move in the i th new variable g i influences each of the original variables d j , j = 1, , N by a factor of a ji .
Let ½ = diag[ ˆ» 1 , » 2 , , ˆ» N ] and define a matrix W = [ w ( t 1 ), w ( t 2 ), , w ( t K )] such that:
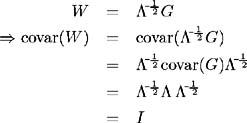
So W is a matrix of independent standard Brownian variables. We may now express the matrix of original variables D , in terms of this matrix of standard Brownian variables as:
or algebraically we may write each d j , j = 1, , N as:
![]() for each observation time k , k = 1, , K which by the definition of d j ( t k ) in (15.8), allows us to write the forward rate process as:
for each observation time k , k = 1, , K which by the definition of d j ( t k ) in (15.8), allows us to write the forward rate process as:
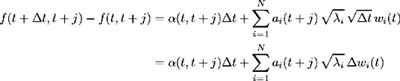
or in continuous time
where a i ( t + j )= a ji for j = 1, , N .
From equation (15.12) we have:
and A ½ is the matrix of principal components of covariance matrix .
As mentioned before, the principal components maximise successive contributions to overall variance. Also, we know » 1 ‰ » 2 ‰ ‰ » N , with the first principal component corresponding to the largest eigenvalue . Therefore the first principal component accounts for the largest percentage of total variance, the second component accounts for the largest percentage of the remaining ( residual ) variance and so on. The greater the covariance between points on the yield curve, the larger the percentage of total variance that will be explained by the first few principal components. So in general, the more principal components required to explain the total variance, the lower the covariance across the yield curve.
While the number of principal components obtained from the analysis detailed in the previous section equals the number of different maturity forward rates used, the hope is that just a few dominant principal components will be required to explain the majority of the variance.
[2] This is consistent with the discussion in Chapter 11 §11.5 concerning the lognormality of forward rates.
[3] This is the methodology used here
[4] This simplified calculation of the covariance matrix implicitly assumes matrix D is mean adjusted and cannot be applied if unadjusted changes in forward rates are used.
[5] Here i and j represent forward rate maturities.
[6] An orthogonal or Hermitian matrix is such that its transpose is equal to its inverse i.e. A ² = A ˆ’ 1 .
EAN: 2147483647
Pages: 132