15.1 Volatility Function Specifications
15.1 Volatility Function Specifications
15.1.1 Well known volatility functions
Some simple functional forms, many relating to volatility specifications in earlier short rate models, have been investigated for goodness of fit.
-
ƒ ( ‰ , t , T ) ‰ ƒ where ƒ is a constant. This is the volatility function of the Ho-Lee model as examined in Chapter 11 §11.7. It leads to a highly tractable but unrealistic model. In Chapter 11 equation (11.38), the forward rate process is shown to be:

The constant volatility across maturities is at odds with the declining volatility with increasing maturity observed in most economies. Additionally the drift increases with maturity, causing long rates to become unbounded.
-
ƒ ( ‰ , t , T ) ‰ ƒ e ˆ’» ( T ˆ’ t ) , where ƒ and » are constants. As shown in §11.9.1, this is the forward rate volatility function corresponding to the Vasicek model. The associated short rate volatility is constant, ƒ ( ‰ , t , t ) ‰ ƒ , but a mean- reverting drift allows the forward rate volatility to decline exponentially with maturity. This specification leads to a tractable but still somewhat unrealistic model.
-
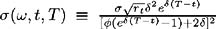 , where and are constants. As derived in §11.8, this is the forward rate volatility resulting from the CIR model specifications. As demonstrated in Chapter 11 §11.9.2 the short rate is Markovian.
, where and are constants. As derived in §11.8, this is the forward rate volatility resulting from the CIR model specifications. As demonstrated in Chapter 11 §11.9.2 the short rate is Markovian. -
ƒ ( ‰ , t , T ) ‰ ƒ f, ƒ ˆ f , ƒ + ƒ 1 ( T ˆ’ t ), ( ƒ + ƒ 1 ( T ˆ’ t )) f . Aminand Morton [ 2 ] investigated these functional forms as well as those in (1) and (2) above as special cases of the general volatility function:
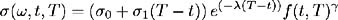
They examined parameter stability, goodness of fit to market prices and possibilities of exploiting any mispricing indicated by the models. Although the two-parameter volatility functions displayed better fit to market prices, the associated parameters were less stable over time and were not as consistent in allowing abnormal profits to be earned from indicated mispricing.
15.1.2 Gaussian volatility functions
The forward rate process (equation (11.32) of Chapter 11) is Gaussian if the volatilities are deterministic functions of t and T only, hence:
with ƒ i ( t , T ), i = 1, , n deterministic functions of t and T . This implies f ( t , T ) is normally distributed and hence discount bond prices are lognormally distributed. This attribute allows certain simple contingent claims to be priced using analytical formulae. The time t price of a T 1 maturity European call option on a discount bond with maturity T 2 and strike X , has solution:

where, as defined in (11.11)
As with other Gaussian interest rate models, there is a positive probability of negative interest rates, which leaves this specification open to criticism.
15.1.3 Markovian Functional Forms
The conditions that must be satisfied to ensure Markovian short rate dynamics are detailed in §11.9. The specific volatility functions of the Ho-Lee, Vasicek and CIR models satisfy these conditions. Ritchken and Sankarasubramanian (RS) [ 48 ] and Li, Ritchken and Sankarasubramanian [ 37 ] recognise that these conditions are restrictive since they may impose undesirable characteristics on the term structure evolution and restrict the shape of initial term structure that may be fitted. They identify a broad class of volatility functions that allow contingent claims to be priced by a two-state variable Markovian model. The path dependence is not fully removed, but captured within an additional variable. This class of volatility functions is of the form:
where ƒ ( t , t ) is the short rate volatility and ( t ) is an exogenously specified deterministic function. RS allow a second variable:
which represents the accumulated variance up to date t and houses the path dependence. The link between forward rate volatilities and the short rate volatility is explicitly defined by the parameter { ( x )x ‰ 0} and so forward rate volatilities may fluctuate with the level of the short rate. However, forward rate dependent volatilities (as investigated by Amin and Morton [ 2 ]) are excluded from this framework.
No restrictions are placed on the short rate volatility which could depend on the entire history of term structures, hence the short rate volatility may be a function of both r ( t ) and ( t ). Specifically consider
Allowing ³ =0and ³ = 0.5 results in special cases of this class corresponding to the Vasicek [ 50 ] and CIR [ 18 ] models.
The Hull-White extended Vasicek model (Chapter 7) displays short rate dynamics and forward rate volatility of the form:
which clearly fits within the RS framework.
Forward rate volatility term structures implied by market prices of traded instruments often display a humped shape, being higher for shorter maturities, see Heath [ 26 ] and Brigo and Mercurio [ 12 ]. This volatility structure may be achieved within the RS framework by choosing ( x )tobeofanappropriate form. Alternatively, Mercurio and Moraleda (see [ 12 ]) model a humped volatility structure by specifying the forward rate volatility as:
However, this volatility is not of RS form.
EAN: 2147483647
Pages: 132