Cryptography: Theory and Practice:Hash Functions | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

THEOREM 7.3

Suppose h : 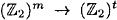is a strongly collision-free hash function, where m ≥ t + 2. Then the function h* : , as constructed in Figure 7.4, is a strongly collision-free hash function.

PROOF Suppose that we can find x ≠ x′ such that h*(x) = h*(x′). Given such a pair, we will show how we can find a collision for h in polynomial time. Since h is assumed to be strongly collision-free, we will obtain a contradiction, and thus h* will be proved to be strongly collision-free.

Denote

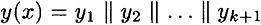
and

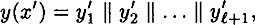
where x and x′ are padded with d and d′ 0’s, respectively, in step 2. Denote the values computed in steps 4 and 5 by g₁,...,g_k+1 and 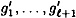, respectively.

We identify two cases, depending on whether or not |x| ≡ |x′| (mod m-t-1).

case 1:

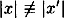(mod m - t - 1).

Here d ≠ d′ and 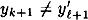. We have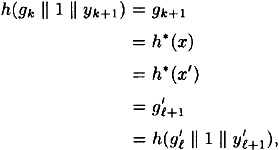

which is a collision for h since .

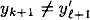case 2: |x| ≡ |x′| (mod m - t - 1).

It is convenient to split this into two subcases:

case 2a: |x| = |x′|.

Here we have 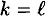and . We begin as in case 1:

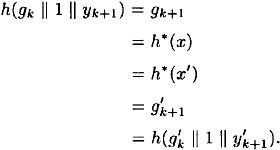
If 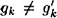, then we find a collision for h, so assume 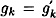. Then we have

Either we find a collision for h, or and 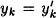. Assuming we do not find a collision, we continue working backwards, until finally we obtain

If 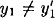, then we find a collision for h, so we assume . But then 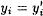for 1 ≤ i ≤ k + 1, so y(x) = y(x′). But this implies x = x′ since the mapping 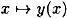is an injection. Since we assumed x ≠ x′, we have a contradiction.

Figure 7.5 Extending a hash function h to h^* (m = t + 1)

case 2b: |x| ≠ |x′|.

Without loss of generality, assume |x′| > |x|, so 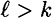. This case proceeds in a similar fashion as case 2a. Assuming we find no collisions for h, we eventually reach the situation where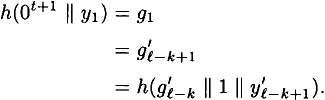

But the (t + 1)st bit of 0^t+1 || y₁ is a 0 and the (t + 1)st bit of is a 1. So we find a collision for h.

Since we have considered all possible cases, we have the desired conclusion.

The construction of Figure 7.4 can be used only when m ≥ t + 2. Let’s now look at the situation where m = t + 1. We need to use a different construction for h*. As before, suppose |x| = n > m. We first encode x in a special way. This will be done using the function f defined as follows:

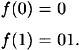
The algorithm to construct h* (x) is presented in Figure 7.5.

The encoding 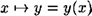, defined in step 1, satisfies two important properties:

1. If x ≠ x′, then y(x) ≠ y(x′) (i.e.,

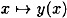is an injection).

2. There do not exist two strings x ≠ x′ and a string z such that y(x) = z || y(x′). (In other words, no encoding is a postfix of another encoding. This is easily seen because each string y(x) begins with 11, and there do not exist two consecutive 1’s in the remainder of the string.)

THEOREM 7.4

Suppose h : 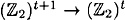is a strongly collision-free hash function. Then the function h* : 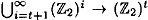, as constructed in Figure 7.5, is a strongly collision-free hash function.

PROOF Suppose that we can find x ≠ x′ such that h* (x) = h* (x′). Denote

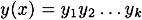
and

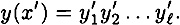
We consider two cases.

case 1:

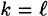As in Theorem 7.3, either we find a collision for h, or we obtain y = y′. But this implies x = x′, a contradiction.

case 2:

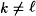Without loss of generality, assume 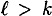. This case proceeds in a similar fashion. Assuming we find no collisions for h, we have the following sequence of equalities: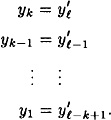

But this contradicts the “postfix-free” property stated above.

We conclude that h* is collision-free.

We summarize the two constructions of in this section, and the number of applications of h needed to compute h*, in the following theorem.

THEOREM 7.5

Suppose h : is a strongly collision-free hash function, where m ≥ t + 1. Then there exists a strongly collision-free hash function

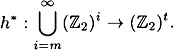
The number of times h is computed in the evaluation of h* is at most

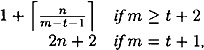
where |x| = n.

7.6 Hash Functions from Cryptosystems

So far, the methods we have described lead to hash functions that are probably too slow to be useful in practice. Another approach is to use an existing private-key cryptosystem to construct a hash function. Let us suppose that 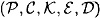is a computationally secure cryptosystem. For convenience, let us assume also that . Here we should have n ≥ 128, say, in order to prevent birthday attacks. This precludes using DES (as does the fact that the key length of DES is different from the plaintext length).

Suppose we are given a bitstring

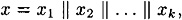
where 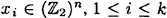. (If the number of bits in x is not a multiple of n, then it will be necessary to pad x in some way, such as was done in Section 7.5. For simplicity, we will ignore this now.)

The basic idea is to begin with a fixed “initial value” g₀ = IV, and then construct g₁,...,g_k in order by a rule of the form

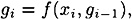
where f is a function that incorporates the encryption function of our cryptosystem. Finally, define the message digest h(x) = g_k.

Table of Contents