THE RUNS TEST

A somewhat advanced technique in recognizing important signals in a process that may be in need of further investigation is the runs test. For each observation Y _t , we associate a 1 if Y _t > Ybar and a 0 if Y _t < . The Y ₁ series then has an associated series of 0's and 1's. For example, suppose that the successive observations are 87, 69, 53, 57, 94, 81, 44, 68, and 77, with mean = 70. Then the sequence of 0's and 1's is 1, 0, 0, 0, 1, 1, 0, 0, 1; four of the nine observations are above the mean, and five are below it. A run is a consecutive sequence of 0's or 1's. The preceding sequence has five runs: 1; 0 0 0; 1 1; 0 0; and 1. The runs test checks whether this is about the right number of runs for a random series.

In general, let T be the number of observations, let T _A be the number of observations above the mean, and let T _B be the number below the mean. Also, let R be the observed number of runs. Then it can be shown that the mean and standard deviation of R for a random series are

and

Also, when T is reasonably large ( T > 20 is suggested), the distribution of R is approximately normal. Therefore, if we define Z by

then Z is approximately normally distributed with mean 0 and standard deviation 1. We can base a statistical test on the value of Z. Specifically, if the absolute value of Z is greater than 1.96, then we can reject the null hypothesis of randomness at the 0.05 significance level. Note that if Z is large and positive, then there are more runs than expected. This means that there is too much zigzagging in the time series graph. On the other hand, if the magnitude of z is large but Z is negative, then there are fewer runs than expected. This situation is more common. Here the observations tend to stay above the mean (or below the mean) for longer stretches than we would expect in a random series. The runs test can also be based on the sample median of the Y's instead of the sample mean.

In the small example above, T = 9, T _A = 4, T _B = 5, and R = 5. Under a randomness hypothesis, the mean and standard deviation of the number of runs, using the two equations, are

E ( R ) = [(9 + 2(4)(5)]/9 = 5.44

and

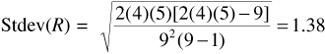
The corresponding Z value is

Z = [5 - 5.44]/1.38 = -.32

This value of Z is certainly not extreme, so there is little evidence of nonran-domness; the observed number of runs is very close to the expected number under a hypothesis of randomness.