THE RELATIONSHIP OF VARIATION TO MEANS TO NORMAL DISTRIBUTION TO CONTROL CHART

Without proof, we present some famous mathematical theorems that allow us to do what we do in SPC.

Theorem 1. The mean of the distribution of sample means is the mean of the universe of individual values from which the samples are taken.

Theorem 2. The variance of the distribution of sample means equals the variance of the universe of individual values divided by n, the size of the sample.

Corollary of Theorem 2. The standard deviation of the distribution of sample means equals 1/ times the standard deviation of the universe of individual values.

Theorem 3 (Chebyshev's Theorem). Given a probability distribution with the mean ¼ and the standard deviation ƒ , the probability of obtaining a value within k standard deviations of the mean is at least 1 - 1/ k ² .

Theorem 4. The form of the distribution of sample means approaches the form of a normal probability distribution as the size of the sample is increased.

Whereas the first three theorems allow us to do comparisons of the means and the population and to evaluate the standard error, the last two allow us to do the analysis of the control chart. In the case of Chabyshev's theorem, we can calculate the probability of any value sigma in relationship to the mean. Chebyshev is telling us that when sigma is small, the probability is high that we will get a value close to the mean. The opposite is also true. (The k can be any positive number, although when k = 1 or less, the theorem becomes trivial.)

Theorem 4 is perhaps the most important and is called the central limit theorem. It is much more powerful than Chebyshev's theorem, and it turns out that it justifies the use of normal curve methods in a wide range of problems. It applies to infinite populations and also to populations in which n, though large, constitutes but a small portion of the population. It is difficult to say exactly how large n must be so that the central limit theorem (CLT) applies, but unless the population has a very unusual shape, n = 30 is usually regarded as sufficiently large.

Taking the samples of a process and plot them as averages is an application of the CLT. The fact that the original data may be coming from nonnormal distribution does not matter. One of the assumptions in SPC is that processes behave in normality patterns and that normality is tested through the CLT. This is why the control limits represent the +3 and -3 standard deviations. This can be seen in Figure 6.13.

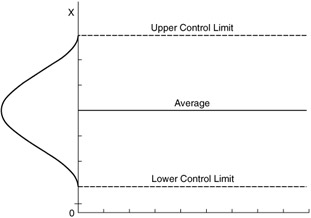
Figure 6.13: The relationship of the normal curve and the control chart.

The reader should notice that the control limits of the control chart are indeed approximately at the ±3 ƒ level and that the center line is the center of the distribution. Also notice that the majority of the points are indeed within the 68% of the distribution. (In reality, when we plot the points on the control chart, we do not have the normal curve next to it. In Figure 6.13, we use it only for explanation purposes.)

A final point about the control charts and variation: Figure 6.14 shows two different control charts with Type I and Type II error. It is significant to see the shift of the mean as well as the distributions. In Figure 6.14a, we see that there are some nonconforming products in the upper side, but the process is in control (Type I error). In Figure 6.14b, we show control, but there is a definite shift of the mean toward the upper side.

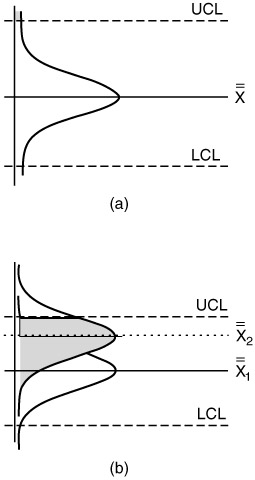
Figure 6.14: A control chart with Type I (a) and Type II (b) error.