ANALYSIS

The purpose of this section is to:

1. Introduce graphical and numerical analysis of experimental data

2. Present a method for estimating a response value and assigning a confidence interval for it

3. Discuss the use and interpretation of signal-to-noise (S/N) ratio calculations

GRAPHICAL ANALYSIS

In the example in Section 2, Timothy and Christine calculated and plotted the average response at each factor level. Since the experimental design they used (an L8) is orthogonal, the average at each level of a factor is equally impacted by the effect of the levels of the other factors. This allows the graphical approach to have direct usage. This example from section 2 is shown in Table 9.18. The factor level plots are shown in Figure 9.17.

Table 9.18: L8 with Test Results

Test Number	Levels for Each Suspected Factor for Each of 8 Tests							Test Result
	C1	C2	C7	C11	C13	C15	C16
1	1	1	1	1	1	1	1	10
2	1	1	1	2	2	2	2	13
3	1	2	2	1	1	2	2	15
4	1	2	2	2	2	1	1	17
5	2	1	2	1	2	1	2	14
6	2	1	2	2	1	2	1	16
7	2	2	1	1	2	2	1	19
8	2	2	1	2	1	1	2	21
Note: The C numbers (e.g., C11, C13) are factor names .

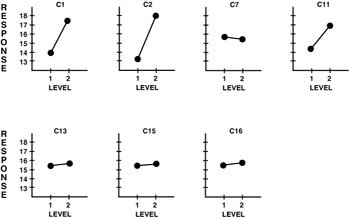
Figure 9.17: Plots of averages (higher responses are better).

Factors C1, C2 and C11 clearly have a different response for each of their two levels. The difference between levels is much smaller for the other factors. If the goal of the experiment was to identify situations that minimize or maximize the response, C1, C2 and C11 are important while the others are not.

Graphical analysis is a valid, powerful technique that is especially useful in the following situations:

1. When computer analysis programs are not available

2. When a quick picture of the experimental results is desired

3. As a visual aid in conjunction with computer analysis

Once the experiment has been set up correctly, the graphical analysis can be easily used and can point the way to improvements.

ANALYSIS OF VARIANCE (ANOVA)

As was mentioned earlier, mathematical calculations and detailed discussions will not be included in this chapter. The interested reader should consult Volume V of this series or references listed in the Bibliography for rigorous mathematical discussions. The approach given here will focus on the interpretation of the ANOVA analysis.

ANOVA is a matrix analysis procedure that partitions the total variation measured in a set of data. These partitions are the portions that are due to the difference in response between the levels of each factor. The number of degrees of freedom (df) associated with an experimental setup is also the maximum number of partitions that can be made. Consider the L8 experiment from section 2 that was illustrated previously in the graphical analysis section. Table 9.19, which is an ANOVA table, summarizes the analysis.

Table 9.19: ANOVA Table

Column	Source	df	SS	MS	F Ratio	S'	%
1	C1	1	28.125	28.125	225	28.000	33.38
2	C2	1	45.125	45.125	361	45.000	53.65
3	C7	1*	0.125	0.125
4	C11	1	10.125	10.125	81	10.000	11.92
5	C13	1*	0.125	0.125
6	C15	1*	0.125	0.125
7	C16	1*	0.125	0.125
Error
(pooled error)		4	0.500	0.125		0.875	1.04
Total		7	83.875	11.982		83.875
Note: df = degrees-of-freedom; MS = mean square; SS = sum of squares.

The column number shows to what column of the orthogonal array the source (factor) was assigned. Normally, the column number is not shown in an ANOVA table. The df column shows the df(s) associated with the factor in the source column. The SS column contains the sums of squares. The SS is a measure of the spread of the data due to that factor. The total SS is the sum of the SS due to all of the sources. The MS or mean square column shows the SS/df for each source. The MS is also known as the variance.

The row with "error" in the source column is left blank in this experiment. If one of the columns had not been assigned or if the experiment had been replicated, then the unassigned dfs would have been used to estimate error. Error is the non- repeatability of the experiment with everything held as constant as possible. The ANOVA technique compares the variability contribution of each factor to the variability due to error. Factors that do not demonstrate much difference in response over the levels tested have a variability that is not much different from the error estimate. The df and SS from these factors are pooled into the error term . Pooling is done by adding the df and SS into the error df and SS. Pooling the insignificant factors into the error can provide a better estimate of the error.

Initially, no estimate of error was made in the L8 example because no unassigned columns or repetitions were present. Because of this, a true estimate of the error could not be made. However, the purpose of the experiment was to identify the factors that have a usable difference in response between the levels. In this experiment, the factors with relatively small MS were pooled and called "error." Pooling requires that the experimenter judge which differences are significant from an operational standpoint. This judgment is based on the prior knowledge of the system being studied. In the example, factors C7, C13, C15, and C16 have much lower MS than do the other factors and are pooled to construct an error estimate. The * next to a df indicates that the df and SS for that factor were pooled into the error term.

The F ratio column contains the ratio of the MS for a source to the MS for the pooled error. This ratio is used to statistically test whether the variance due to that factor is significantly different from the error variance. As a quick rule of thumb, if the F ratio is greater than three, the experimenter should suspect that there is a significant difference. Dr. Taguchi does not emphasize the use of the F ratio statistical test in his approach to DOE. A detailed description of the use of the F test can be found in Box, Hunter, and Hunter (1978), and a practical explanation is included in Volume V of this series.

In the determination of the SS of a factor, the non-repeatability of the experiment is still present. The number in the "S" column is an attempt to totally remove the SS due to error and leave the "pure" SS that is due only to the source factor. The error MS times the df is subtracted from the SS to leave the pure SS or S' value for a factor. The amount that is subtracted from each non-pooled factor is then added to the pooled error SS and the total is entered as the error S'. In this way the total SS remains the same.

The % column contains the S' value divided by the total SS times 100%. This gives the percent contribution by that factor to the total variation of the data. This information can be used directly in prioritizing the factors. In the experiment that has been discussed, C2 makes the greatest contribution, C1 contributes less, and C11 contributes still less. It can be argued that the graphical analysis can display those conclusions quite well. In more complicated experiments with many factors and factors with a large number of levels, however, the ANOVA table can display the analysis in a more concise form and quickly lead the experimenter to the most important factors.

ESTIMATION AT THE OPTIMUM LEVEL

The ANOVA table is used to identify important factors. The experimenter refers to the average response at each level of the important factors to choose the best combination of factor levels. All of the best levels can be combined to estimate the responses at the best factor combination. Consider the case where the second level of factor A (A2), the third level of factor B (B3), the first level of factor C (C1), and the interaction of C1 and D1 are determined to be the best combination of factors. An estimate of the response at these conditions can be made using the equation:

where = the average response of all the data; = the average of the data run at A ₂ ; = the average of the data run at B ₃ ; = the average of the data run at C ₁ ; and = the average of the data run at D ₁ .

Each factor that is a significant contributor appears in a manner similar to A ₂ , B ₃ and C ₁ above. The term in brackets [ ] addresses the optimum level of the CD interaction and is an example of the way in which interactions are handled.

CONFIDENCE INTERVAL AROUND THE ESTIMATION

A 90% confidence interval can be calculated for confirmatory tests using the equation:

where F _1,dfe,.05 is a value from an F statistical table. The F values are based on two different degrees of freedom and the desired confidence. In this case, the first degree of freedom is always 1 and the second is the degree of freedom of the pooled error (dfe). The desired confidence is .05 since .05 in each direction ( ±) sums to a 10% confidence. MS _e is the mean square of the pooled error term; n _r is the number of confirmatory tests to be run; and n _e is the effective number of replications and is calculated as follows :

n _e =

For the that was just considered , n _e is calculated as follows:

Source	df
A	1
B	2
C	1
CD	1
Mean	1
Total	6

Consider that an L36 was run with no repetitions.

n _e = 36/6 = 6.0

INTERPRETATION AND USE

The confidence interval about the estimated value is used as a check when verification runs are made. If the average of the verification runs does not fall within the interval, there is strong reason to believe that a very important factor may have been left out of the experiment.

ANOVA DECOMPOSITION OF MULTI-LEVEL FACTORS

When a factor is tested at two levels, an estimate of the linear change in response between the two levels can be made. When a factor is tested at more than two levels, more complex relationships must be investigated. With a three-level factor, both the linear and quadratic relationships can be investigated. These relationships are demonstrated in Figure 9.18.

Figure 9.18: ANOVA decomposition of multi-level factors.

This relationship is important to consider even when the factor levels are not continuous (e.g., different machines or suppliers). Consider the situation in Figure 9.19. The dotted line is the linear response and indicates no significant difference. However, Supplier 2 is different from Suppliers 1 and 3. This difference can be found only if the quadratic relationship is considered.

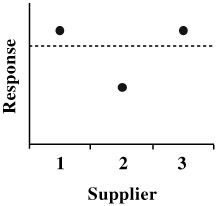
Figure 9.19: Factors not linear.

The number of higher order relationships that can be investigated is determined by the degrees of freedom of the source ” see Table 9.20.

Table 9.20: Higher Order Relationships

Levels of a Factor	df	Relationships
2	1	Linear
3	2	Linear, quadratic
4	3	Linear, quadratic, cubic
5	4	Linear, quadratic, cubic, quartic
etc.

In the ANOVA table, the number of relationships that should be investigated is the same as the df. The total SS for factor is decomposed into parts with unit dfs. These parts are the linear, quadratic, cubic, etc. parts of the relationship. Each part can then be treated separately, and the parts with small MS are pooled into the error term. The type of relationship that remains as significant can guide the experimenter in investigating the level averages.

S/N CALCULATIONS AND INTERPRETATIONS

Control factors and noise factors were introduced in Section 3. Control factors appear in an orthogonal array called an inner array. Noise factors that represent the uncontrolled or uncontrollable environment are entered into a separate array called an outer array. The following example of an L8 linear (control) array with an L4 outer (noise) array was first presented in Section 3. Actual responses and factor names are added here ” see Table 9.21 ” in the development of the example.

Table 9.21: Inner OA (L8) with Outer OA (L4) and Test Results

Test No.	L8							L4	Z	1	2	2	1
	A	B	C	D	E	F	C	(on side)	Y	1	2	1	2
	1	2	3	4	5	6	7		X	1	1	2	2
1	1	1	1	1	1	1	1	Test Results		25	27	30	26
2	1	1	1	2	2	2	2			25	27	21	19
3	1	2	2	1	1	2	2			18	21	19	22
4	1	2	2	2	2	1	1			26	23	27	28
5	2	1	2	1	2	1	2			15	11	12	14
6	2	1	2	2	1	2	1			18	15	17	18
7	2	2	1	1	2	2	1			20	17	21	18
8	2	2	1	2	1	1	2			19	20	20	17

This type of experimental setup and analysis evaluates each of the control factor choices (L8 array factors) over the expected range of the uncontrollable environment (L4 array factors). This assures that the optimal factor levels from the L8 array will be robust. An S/N can be calculated for each test situation. These S/N ratios are then used in an ANOVA to identify the situation that maximizes the S/N.

Smaller-the-Better (STB)

The following S/N ratios are calculated for the STB situation using the equations given in Section 4 and assuming that the optimum value is zero and that the responses shown represent deviations from that target:

Test Number	STB S/N
1	28.65
2	27.32
3	26.05
4	28.32
5	22.34
6	24.63
7	25.61
8	25.59

The S/N ratios for testing situations are then analyzed using an ANOVA table. The STB ANOVA table for the example is shown in Table 9.22. The ANOVA table indicates that factors A, G, and C are the most significant contributors. Inspection of the level averages shows that the highest S/N values (least negative), in order of contribution, occur at A ₂ , G ₂ , C ₂ , D ₁ , B ₁ . Estimation of the S/N at the optimal levels can be made from the S/N level averages using the technique discussed earlier in this section. Likewise, estimation of the raw data average response at the optimal level can be made from the response level averages at the optimal S/N factor levels.

Table 9.22: The STB ANOVA Table

Source	df	SS	MS	F Ratio	S'	%
A	1	18.487	18.487	84.803	18.269	61.53
B	1	0.864	0.864	3.963	0.646	2.18
C	1	4.232	4.232	19.413	4.014	13.53
D	1	1.295	1.295	5.940	1.077	3.63
E	1*	0.223	0.223
F	1*	0.213	0.213
G	1	4.362	4.362	20.009	4.144	13.96
Error
(pooled error)	2	0.436	0.218		1.526	5.14
Total	7	29.676	4.239

Larger-the-Better (LTB)

The same data will be used to demonstrate the LTB notation. In this case, the optimum value is infinity. Examples of this include strength or fuel economy. The following S/N ratios are calculated using the LTB equation given in Section 4.

Test Number	LTB S/N
1	28.57
2	26.98
3	25.94
4	28.23
5	22.08
6	24.54
7	25.48
8	25.52

The S/N ratios for testing situations are then analyzed using an ANOVA table. The LTB ANOVA table for the example is shown in Table 9.23. Inspection of the ANOVA table and the level averages shows that the highest S/N values occur at A ₁ , G ₁ , C ₁ , D ₂ , B ₂ . Interpretation of the LTB analysis is similar to that of the STB analysis.

Table 9.23: The LTB ANOVA Table

Source	df	SS	MS	F Ratio	S'	%
A	1	18.292	18.292	55.442	17.966	58.99
B	1	1.121	1.121	3.397	0.791	2.60
C	1	4.160	4.160	12.605	3.830	12.58
D	1	1.271	1.271	3.852	0.941	3.09
E	1*	0.396	0.396
F	1*	0.264	0.264
		4.947	4.947	14.991	4.617	15.16
G	1
Error
(pooled error)	2	0.660	0.330		2.310	7.59
Total	7	30.454	4.351

Nominal the Best (NTB)

Analysis of the NTB experiment is a two-part process. Again, the same data will be used to illustrate this approach. The target value will be assumed to be 24 in this case.

The S/N values are analyzed. The following S/N are calculated:

Test Number	STB S/N
1	21.93
2	15.96
3	20.78
4	21.60
5	17.03
6	21.59
7	20.33
8	22.56

• The S/N ratios for testing situations are then analyzed using an ANOVA table. The NTB ANOVA table for the example is shown in Table 9.24.

  Table 9.24: The NTB ANOVA Table

  Source	df	SS	MS	F Ratio	S'	%
  A	1*	0.193	0.193
  B	1	9.618	9.618	54.339	9.441	23.10
  C	1*	0.006	0.006
  D	1*	0.333	0.333
  E	1	17.816	17.816	100.655	17.639	43.16
  F	1	2.477	2.477	13.994	2.300	5.63
  G	1	10.424	10.424	58.893	10.247	25.07
  Error
  (pooled error)	3	0.532	0.177		1.240	3.03
  Total	7	40.867	5.838

• The ANOVA table and the level averages indicate that E ₁ , G ₁ , B ₂ , F _l are the optimal choices from an S/N standpoint. These are the factor choices that should result in the minimum variance of the response.

• The ANOVA analysis and level averages of the raw data are then investigated to determine if there are other factors that have significantly different responses at their different levels but are not significant in the S/N analysis. These factors can be used to tune the average response to the desired value but do not appreciably affect the variability of the response. The ANOVA table of the raw data is shown in Table 9.25. From this ANOVA table, it can be seen that the significant contributors to the observed variability of the data averages are the factors A, G, C, D, and F. This can be combined with the S/N analysis and interpreted as follows:

  1. Factors that influence variability only ” B, E

  2. Factors that influence both variability and average response ” G

  3. Factors that influence the average only ” A, C

  4. Factors that have little or no influence on either variability or average response - D, F

  Table 9.25: Raw Data ANOVA Table

  Source	Df	SS	MS	F Ratio	S'	%
  A	1	392.000	392.000	84.940	387.385	53.95
  B	1*	8.000	8.000
  C	1	72.000	72.000	15.601	67.385	9.39
  D	1	18.000	18.000	3.900	13.385	1.86
  E	1*	2.000	2.000
  F	1	18.000	18.000	3.900	13.385	1.86
  G	1	98.000	98.000	21.235	93.385	13.01
  X	1*	0.125	0.125
  Y	1*	3.125	3.125
  Z	1*	0.000	0.000
  Error	21	106.750	5.083
  (pooled error)	26	120.000	4.615		143.075	19.93
  Total	31	718.000	23.161

The results from this experiment indicate that factors B, E, and G should be set to the levels with the highest S/N. Factor G should be set to the level with the highest S/N rather than using it to tune the average since its relative contribution to S/N variability is greater than its contribution to the variability of raw data. This decision might change based on cost implications and the ability to use factors A and C to tune the average response. Factors A and C should be investigated to determine if they can be set to levels that will allow the target value of 24 to be attained. This may be possible with factors that have continuous values. Factors with discrete choices such as supplier or machine number cannot be interpolated. Factors D and F should be set to the levels that are least expensive. A series of confirmation runs should be made when the optimum levels have been determined. The average response and S/N should be compared to the predicted values.

COMBINATION DESIGN

Combination design was mentioned in Section 3 as a way of assigning two two-level factors to a single three-level column. This is done by assigning three of the four combinations of the two two-level factors to the three-level factor and not testing the fourth combination. As an example, two two-level factors are assigned to a three-level column as in Table 9.26.

Table 9.26: Combination Design

Factor A	Factor B	Three Level Column Combined Factor (A.B)
1	1	1
2	1	2
2	2	3

Note that the combination A ₁ B ₂ is not tested. In this approach, information about the A.B interaction is not available, and many ANOVA computer programs are not able to break apart the effect of A and B.

The sum of squares (SS) in the ANOVA table that is due to factor A.B contains both the SS due to factor A and the SS due to factor B. These two SSs are not additive since the factors A and B are not orthogonal. This means:

SS _AB ‰  SS _A + SS _B

The SS of A and B can be calculated separately as follows:

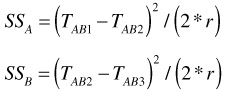
where T _AB1 = the sum of all responses run at the first level of AB; T _AB2 = the sum of all responses run at the second level of AB; T _AB3 = the sum of all responses run at the third level of AB; and r = the number of data points run at each level of AB.

The MS of A and B then can be separately compared to the error MS to determine if either or both factors are significant. The df for both A and B is 1. If one of the factors is significant and the other is not, the ANOVA should be rerun with the significant factor shown with a dummy treatment and the other factor excluded from the analysis.

The following factors will be evaluated using an L9 orthogonal array:

Factor	Number of Levels
A	2
B	2
C	3
D	3
E	3

A and B will be combined into a single three-level column. The test array and results are shown in Table 9.27.

Table 9.27: L9 OA with Test Results

A	B	A.B	C	D	E	Test Results		Sum of the Test Results
1	1	1	1	1	1	7	10	17
1	1	1	2	2	2	3	6	9
1	1	1	3	3	3	5	3	8
2	1	2	1	2	3	22	18	40
2	1	2	2	3	1	13	15	28
2	1	2	3	1	2	9	8	17
2	2	3	1	3	2	12	16	28
2	2	3	2	1	3	12	10	22
2	2	3	3	2	1	15	12	27

The sum of the data at each level of AB is: for AB = 1, the sum is 17 + 9 + 8 = 34; for AB = 2, the sum is 40 + 28 + 17 = 85; for AB = 3, the sum is 28 + 22 + 27 = 77.

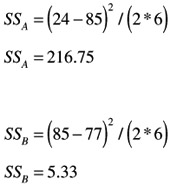
The ANOVA table is for the data shown ” see Table 9.28. The decomposed SS for A and B are shown in parentheses and are not added into the total SS.

Table 9.28: ANOVA Table

Source	df	SS	MS	F Ratio	S'	%
A.B	2	250.778	125.389	31.347	242.778	53.50
(A)	1	(216.750)	216.750	54.188
(B)	1	(5.333)	5.333	1.333
C	2	100.778	50.389	12.597	92.778	20.45
D	2	33.778	16.889	4.222	25.778	5.68
E	2	32.444	16.222	4.056	24.444	5.39
Error	9	36.000	4.000
(pooled error)	9	36.000	4.000		68.000	14.99
Total	17	453.778	26.693

The F ratio for factor B indicates that the effect of the change in factor B on the response is insignificant. Factor B is excluded from the analysis and factor A is analyzed with a dummy treatment. The ANOVA table for this analysis is shown in Table 9.29. The analysis continues using the techniques described in this section.

Table 9.29: Second Run of ANOVA

Source	df	SS	MS	F Ratio	S'	%
A	1	245.444	245.444	59.386	241.311	53.18
C	2	100.778	50.389	12.192	92.512	20.39
D	2	33.778	16.889	4.086	25.512	5.62
E	2	32.444	16.222	3.925	24.178	5.33
Error	10	41.334	4.133
(pooled error)	10	41.334	4.133		70.265	15.48
Total	17	453.778	26.693

 

MISCELLANEOUS THOUGHTS

The purpose of most DOEs is to predict what the response will be at the optimum condition. Confirmatory tests should be run to assure the experimenter that the projected results are valid. Sometimes, the results of the confirmatory tests are significantly different from the projected results. This can be due to one or more of the following:

• There was an error in the basic assumptions made in setting up the experiment.

• Not all of the important factors were controlled in the experiment.

• The factors interacted in a manner that was not accounted for.

• The response that was measured was not the proper response or was only a symptom of something more basic (see Section 2).

• An important noise factor was not included in the experiment (e.g., the experimental tests were run on sunny days while the confirmatory tests were run on a rainy day).

• The experimental test equipment is not capable of providing consistent, repeatable test results.

• A mistake was made in setting up one or more of the experimental tests.

The experimenter who is faced with data that does not support the prediction is forced to ask which of these problems affected the results. It is important that all of these problems be considered and investigated, if appropriate. If two or more of these problems coexisted, correcting only one problem may not improve the experimental results.

Even though it may seem that the experiment was a failure, that is not necessarily true. Experimentation should be considered an organized approach to uncovering a working knowledge about a situation. The "failed" experiment does provide new knowledge about the situation that should be used in setting up the next iteration of experimental testing.

The prior statement may sound too idealistic for the "real" world where deadlines are very important. A failed experiment may cause some people to doubt the usefulness of the DOE approach and extol the virtues of traditional one-factor-at-a-time testing. However, all of the problems listed above that could cause a DOE to fail will also cause a one-factor-at-a-time experiment to fail. In DOE, the problem will be found fairly early since relatively few tests are run. In one-factor-at-a-time testing, the problem may not surface until many tests have been run, or the problem may not even be identified in the testing program. In this case, the problem may not show up until production or field use.

The importance of meeting real-world deadlines makes the planning stage of the experiment critical. Proper planning, including consideration of the experience and knowledge of experts, will enable the experimenter to avoid many of the possible problems. Deadlines are never a good excuse for not taking the time to adequately plan an experiment.

AN EXAMPLE

The data used to demonstrate the S/N calculations in this section will be analyzed here using the approach, NTB _II S/N = -10 log (s ² ) = -20 log (s). This approach was discussed earlier in this chapter. The data set is repeated in Table 9.30.

Table 9.30: L8 with Test Results and S/N Values

Test No.	L8							Z	1	2	2	1
	A	B	C	D	E	F	C	Y	1	2	1	2		-20
	1	2	3	4	5	6	7	X	1	1	2	2	S	log(s)
1	1	1	1	1	1	1	1	Test	25	27	30	26	2.16	-6.690
2	1	1	1	2	2	2	2	Results	25	27	21	19	3.65	-11.249
3	1	2	2	1	1	2	2		18	21	19	22	1.83	-5.229
4	1	2	2	2	2	1	1		26	23	27	28	2.16	-6.690
5	2	1	2	1	2	1	2		15	11	12	14	1.83	-5.229
6	2	1	2	2	1	2	1		18	15	17	18	1.41	-3.010
7	2	2	1	1	2	2	1		20	17	21	18	1.83	-5.229
8	2	2	1	2	1	1	2		19	20	20	17	1.41	-3.010

The S/N ratios for the testing situations are then analyzed using an ANOVA table. The NTB _II ANOVA table for the example is shown in Table 9.31. To help interpret the ANOVA table, the level standard deviation averages and the level S/N averages are shown for the significant factors in Table 9.32.

Table 9.31: ANOVA Table for Data from Table 9.30

Source	df	SS	MS	F Ratio	S'	%
A	1	22.379	22.379	24.746	21.474	44.90
B	1	4.531	4.531	5.010	3.627	7.58
C	1	4.531	4.531	5.010	3.627	7.58
D	1*	0.313	0.313
E	1	13.670	13.670	15.117	12.766	26.69
F	1*	1.200	1.200
G	1*	1.200	1.200
Error
(pooled error)	3	2.713	0.904		6.330	13.24
Total	7	47.823	6.832

Table 9.32: Significant Figures from Table 9.31

Factor	Level	Average Standard Deviation	NTB II S/N
A	1	2.36	-7.465
	2	1.61	-4.120
B	1	2.12	-6.545
	2	1.79	-5.039
C	1	2.12	-6.545
	2	1.79	-5.039
E	1	1.67	-4.485
	2	2.26	-7.099

To give a visual impact of the spread of the data and what the above table really means, it would be wise to plot the data for each factor level. The plots of the average standard deviation by factor level are shown in Figure 9.20.

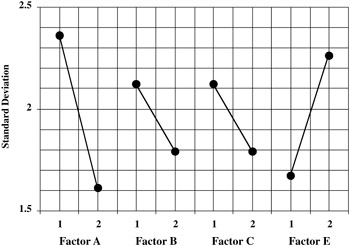
Figure 9.20: Plots of the average standard deviation by factor level.

The ANOVA table and the level average standard deviations indicate that A ₂ B ₂ C ₂ E ₁ are the optimal choices from an NTB _II S/N standpoint. The analysis of the raw data remains the same as shown in the chapter. The average level of the response should be targeted using the results of the raw data analysis. This is true regardless of whether the goal is as small as possible, as large as possible, or to meet a specific value. The variance should be minimized by maximizing the NTB _II S/N. The experimenter must make the trade-off between the choice of factor levels that adjust the response average and the choice of factor levels that minimize the variance of the response.

A comparison of the results of the two methods shows clear differences. As an example, for the situation where a specific value is targeted (NTB), the factor level choices are: NTB ” B ₂ E ₁ G ₁ to minimize variability, A and C set to achieve target; NTB _II ” B ₂ E ₁ to minimize variability, G set to achieve target. If the target is attainable using factor G, use A ₂ C ₂ to minimize variability, otherwise , set C and/or A to achieve target.

 

There is no complete agreement among statisticians and DOE practitioners as to which approach gives better results. As a general rule, the reader is encouraged to:

1. Plot the data including raw and/or transformed values, level averages and standard deviations, and any other information that seems appropriate. One picture is worth a thousand words.

2. Analyze the data using the appropriate analysis techniques.

3. Compare the results to the data plots in order to determine which set of results makes the most sense. Perform this comparison fairly and resist the temptation to choose the results solely on whether they support convenient conclusions.

4. Run confirmation tests.

DOE is a powerful tool that can help the experimenter get the most out of scarce testing resources. However, as with any powerful tool, care must be taken to understand how to use the tool and how to interpret the results.