8.3 The E-Business Workload

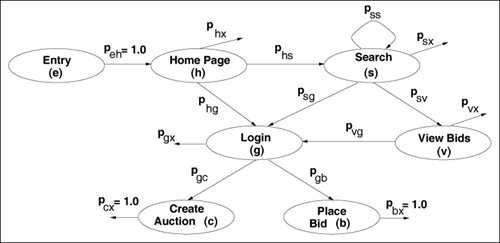
The workload of the online auction site is characterized by its customer behavior using a Customer Behavior Model Graph (CBMG) [4]. This graph represents the behavior of a customer during a session, which is defined as a sequence of consecutive requests coming from the same customer during a single visit to a site. A CBMG has one node for each state in which a customer can be found during a session. Arcs between nodes indicate possible transitions between states. Figure 8.2 illustrates the CBMG for the auction site. The Entry state represents the customer before entering the site. Arc label p_i,j represents the probability of transitioning directly from state i to state j. State x (not explicitly shown in Fig. 8.2) represents the Exit state. Once in the site, a customer can exit from any state i with probability p_i,x.

Figure 8.2. Customer Behavior Model Graph (CBMG) for the auction site.

The CBMG of Fig. 8.2 has the following eight states: Entry (e), Home Page (h), Search (s), View Bids (v), Login (g), Create Auction (c), Place Bid (b), and Exit (x). The transitions between states are labeled by the probability that the transition occurs. For example, in Fig. 8.2, the probability that a customer will move to the Search (s) state after visiting the Home Page (h) is given by p_hs.

The CBMG can be used to compute the average number of visits, V_j, to each state j during a session. V_j can be computed from knowing the average number of visits to the other states and the transition probabilities. For instance, suppose state j can only be entered into from state i. Knowing V_i, V_j can be computed as V_j = V_i x p_i,j. Said differently, V_j can be computed directly from the number of visits made to j's upstream neighbors and the probabilities of visiting j next. For example, Fig. 8.2, to compute V_g, one needs to know V_h, V_s, and V_v as well as the probabilities of going from states h, s, and v to state g. One can then write down the equation

This leads to a set of equations, one for every state. Applied to all states of the CBMG of Fig. 8.2, the following set of equations result.

Equation 8.3.1

Equation 8.3.2

Equation 8.3.3

Equation 8.3.4

Equation 8.3.5

Equation 8.3.6

Equation 8.3.7

Combining Eqs. (8.3.2) and (8.3.3) yields,

Equation 8.3.8

The values of V_v, V_g, V_c, and V_b follow immediately from previously obtained values. In general, the set of equations derived from a CBMG is a system of linear equations (see Exercise 8.3) that can be easily solved using any statistical and/or mathematical software package.

Not all customer sessions of an e-commerce site are similar in terms of user navigational patterns. For example, some sessions may be characterized by a "window-shopping" type of behavior while others may reflect a navigational pattern of more serious buyers. Therefore, when characterizing the workload of an e-commerce site, one may find that the set of sessions can be clustered into groups of sessions that exhibit similar navigational patterns [5]. Each such cluster is represented by its own CBMG.

The characterization of the workload of the online auction site described in this case study yields two different types of sessions, session type A and session type B. A CBMG can be represented by an n x n matrix of transition probabilities between its n states. The transition probability matrices for the CBMGs of these two types of sessions are given in Tables 8.1 and 8.2. Twenty five percent of all sessions are of type A and the remaining are of type B.

Table 8.1. Matrix of Transition Probabilities for the CBMG of Type A Sessions

	(e)	(h)	(s)	(v)	(g)	(c)	(b)	(x)
Entry (e)	0.00	1.00	0.00	0.00	0.00	0.00	0.00	0.00
Home (h)	0.00	0.00	0.70	0.00	0.10	0.00	0.00	0.20
Search (s)	0.00	0.00	0.40	0.20	0.15	0.00	0.00	0.25
View Bids (v)	0.00	0.00	0.00	0.00	0.65	0.00	0.00	0.35
Login (g)	0.00	0.00	0.00	0.00	0.00	0.30	0.60	0.10
Create Auction (c)	0.00	0.00	0.00	0.00	0.00	0.00	0.00	1.00
Place Bid (b)	0.00	0.00	0.00	0.00	0.00	0.00	0.00	1.00
Exit (x)	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00

Table 8.2. Matrix of Transition Probabilities for the CBMG of Type B Sessions

	(e)	(h)	(s)	(v)	(g)	(c)	(b)	(x)
Entry (e)	0.00	1.00	0.00	0.00	0.00	0.00	0.00	0.00
Home (h)	0.00	0.00	0.70	0.00	0.10	0.00	0.00	0.20
Search (s)	0.00	0.00	0.45	0.15	0.10	0.00	0.00	0.30
View Bids (v)	0.00	0.00	0.00	0.00	0.40	0.00	0.00	0.60
Login (g)	0.00	0.00	0.00	0.00	0.00	0.30	0.55	0.15
Create Auction (c)	0.00	0.00	0.00	0.00	0.00	0.00	0.00	1.00
Place Bid (b)	0.00	0.00	0.00	0.00	0.00	0.00	0.00	1.00
Exit (x)	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00

Using Eqs. (8.3.1)-(8.3.7) on the CBMGs of Tables 8.1 and 8.2 yields the average number of visits to each state shown in Table 8.3. Sessions of type A are characterized by a higher number of visits to most states, in particular to states c and b (i.e., create auction and place bid) that tend to bring business to the auction site.

Table 8.3. Average Visits for Sessions of Type A and B

State	Session A	Session B
Ve	1.000	1.000
Vh	1.000	1.000
Vs	1.167	1.273
Vv	0.233	0.191
Vg	0.427	0.304
Vc	0.128	0.091
Vb	0.256	0.167