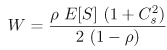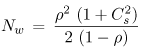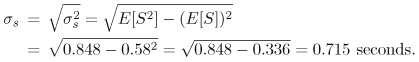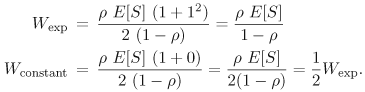11.4 The MG1 Queue

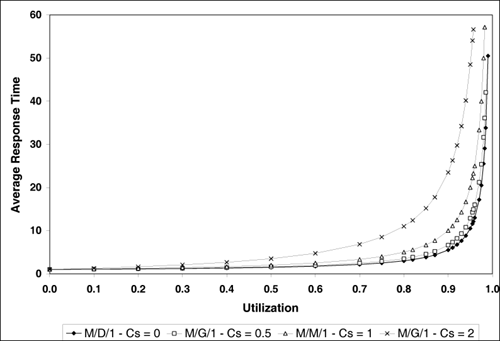
11.4 The M/G/1 Queue

A well-studied special case of the G/G/1 queue occurs when the interarrival times are exponentially distributed but the service time distribution is any arbitrary (i.e., general) distribution. This queue is called an M/G/1 queue. The basic result for an M/G/1 queue, known as the Pollaczek-Khintchine (P-K) formula [2] for the average waiting time W, is

Equation 11.4.14

where is the square of the coefficient of variation of the service time distribution. [Note: if C_s = 1, the system is an M/M/1 queue.]

The other equations for M/G/1 follow directly from Eqs. (11.2.1)-(11.2.3):

Equation 11.4.15

Equation 11.4.16

Equation 11.4.17

Example 11.3.

Suppose that e-mail messages arrive at an e-mail server from a Poisson process at a rate of 1.2 messages per second. Also suppose that 30% of the messages are processed in 0.1 sec, 50% in 0.3 sec, and 20% in 2 sec. What is the average time E[S] it takes to process a message? What is the average time W a message waits in the queue to be processed? What is the average response time T of an e-mail message? What is the average number of messages N_w waiting in the queue? What is the average number of messages N in the e-mail server?

The average time to process a message is

The utilization of the e-mail server is r = l x E[S] = 1.2 messages/sec x 0.58 seconds/message = 0.696. The coefficient of variation of the processing time, C_s, is the ratio between the standard deviation, s_s, and the average processing time E[S]. The standard deviation is the square root of the variance , which is obtained as , where E[S²] is the second moment of the processing time. In this case,

Thus, the standard deviation s_s is

The coefficient of variation C_s is then C_s = s_s/E[S] = 0.715/0.58 = 1.233. From Eqs. (11.4.14)-(11.4.17):

Example 11.4.

What is the ratio between the average waiting time of an M/G/1 queue with exponentially distributed service times and the waiting time of an M/G/1 queue with constant service times?

The coefficient of variation C_s of a server with an exponentially distributed service time is 1. When the service times are constant, the variance, and therefore the coefficient of variation, is zero. Thus,

Thus, the time spent in the waiting line at an exponential server is on average twice the time spent in the waiting line of a constant speed server.

Figure 11.2 shows various curves of the average response time versus utilization for an M/G/1 queue with E[S] = 1 and for four values of C_s: 0, 0.5, 1, and 2. When C_s = 0, the M/G/1 queue is also referred to as an M/D/1 queue because service times are deterministic. When C_s = 1 service times are exponentially distributed and the resulting queue is an M/M/1 queue. As illustrated in Fig. 11.2 and from Eq. (11.4.15), the average response time increases as a function of the square of the coefficient of variation of the service time. This result indicates that performance degrades as the variability in the server increases. Thus, reducing the uncertainty (i.e., the standard deviation) of the service times placed on devices improves performance.

Figure 11.2. Response time of an M/G/1 queue for various values of C_s.