Chapter 8: B-Spline Surfaces

Derivatives of Polynomial Functions

Recall that a polynomial function is one that takes the form shown in Equation A.1-where the order of the function is the value of the largest exponent.

(A.1) The form of a polynomial function. 

Note that the values of any of the coefficients can be zero. A line is a very simple polynomial in the form shown next .

(A.2) The equation for a line. 

For a line, the change in y with respect to x is just the slope, which can be computed with the simple "rise over run" equation as shown in Figure A.5.

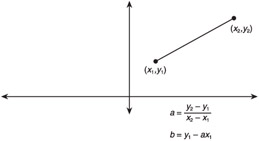
Figure A.5: Computing the slope of a line.

If you know how to compute the slope of a line, you know how to compute the derivative of that line for any value of x . Congratulations, you know a little bit of calculus. However, this obviously doesn't extend to higher-order polynomials like the one shown in Figure A.6. Figure A.6 shows that you can't just pick two points on a curve and compute the correct slope at any given point.

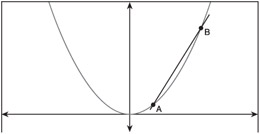
Figure A.6: The slope on a higher-order polynomial.

Still, Figure A.6 reveals the first hint about how you can compute the slope at a certain point. You can think of line AB in the figure as an approximation of the slope at point A. The closer the two points are, the closer the approximate slope is to the correct slope. With that in mind, you can redraw Figure A.6 as Figure A.7.

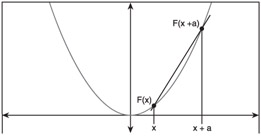
Figure A.7: Reformulating the approximate slope.

Based on Figure A.7 and the equations in Figure A.5, you can say that the approximate slope becomes more and more correct as a approaches zero. Mathematicians write this in the form shown in Equation A.3.

(A.3) The derivative of a function expressed as a limit.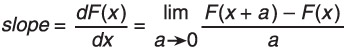 

Here I have introduced the concept of a limit . There are many rules that affect how limits work, but you don't need to know most of them, so I won't explain them here. For simple polynomial functions, the rules are pretty straightforward. Consider Equation A.4 as an example of how the limit applies to a simple polynomial.

(A.4) The derivative of a simple polynomial.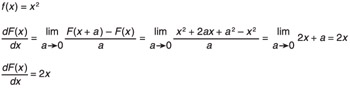 

As you can see, you compute the limit by setting a equal to 0. It may look like you need to divide by 0, but it works out such that you can cancel out a without dealing with the problems associated with dividing by 0. Equation A.4 shows the general operations that will apply to any simple polynomial. I will leave it to you to work out examples of higher-order functions. Keep in mind that I have not given you sufficient information to compute the derivative of Equation A.5. That requires much more information and doesn't really apply to any problems in this book.

(A.5) I haven't told you how to solve this!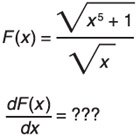 

If you have taken the time to experiment with some simple higher-order polynomials, you will find that each of their derivatives adhere to the following form.

(A.6) Basic derivative of a simple polynomial. 

You may have also noticed that the derivative of sums is the sum of derivatives, meaning that you can break an equation apart, compute the simple derivatives, and add the resulting derivatives back together. This is shown in Equation A.7.

(A.7) The derivative of a sum. 

You now have everything you need to compute the derivatives of the polynomials you'll find in most of the chapters of this book. Figure A.8 shows some examples. The top row is a series of polynomials and the bottom row shows the graphs of their derivatives.

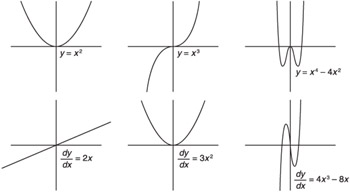
Figure A.8: Derivatives of polynomial functions.

Nearly all of the functions in this book can be expressed as some form of polynomial and in almost all cases it is advantageous to know how to compute the slope along a curve or surface. You now have the basic tools you need to compute those slopes. The explanations here are general and abstract, but you will see concrete uses of these concepts in nearly every chapter.