Exercises

• 9.1 This exercise shows that the plausibility measures Pl₁ and Pl₂ considered in Section 9.1 can be obtained using the construction preceding Theorem 8.4.12.

  1. Show that Pl₁ is the plausibility measure obtained from the probability sequence (μ₁, μ₂, μ₃, …) defined in Section 9.1, using the construction preceding Theorem 8.4.12.

  2. Define a probability sequence (μ₁′, μ₂′, μ₃′, …) from which Pl₂ is obtained using the construction preceding Theorem 8.4.12.

• 9.2 Prove Proposition 9.1.1.

• 9.3 Prove Proposition 9.1.2.

• 9.4 Prove Proposition 9.1.3.

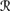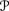
• 9.5 Show that in an SDP system (, 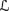_a, π), if the prior Pl_a on runs that generates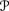 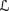_a satisfies Pl4 and Pl5, then so does the agent's plausibility space Pl_a(r, m) at each point (r, m).

• 9.6 Show that a BCS is a synchronous system satisfying CONS in which the agent has perfect recall.

• * 9.7 This exercise expands on Example 9.3.1 and shows that AGM-style belief revision can be understood as conditioning, using a conditional probability measure. As in Example 9.3.1, fix a finite set Φ of primitive propositions and a consequence relation ⊢ 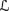for 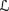^Prop(Φ).

  1. Show that there is a single formula σ such that ⊢ 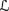iff σ ↠ φ is a propositional tautology.

  2. As in Example 9.3.1, let M = (W, 2^W, 2^W − ∅, μ, π) be a simple conditional probability structure, where π is such that (i) (M, w) ⊨ σ for all w ∈ W and (ii) if σ ∧ ψ is satisfiable, then there is some world w ∈ W such that (M, w) ⊨ ψ. Let K ={ψ : μ([[ψ]]_M) = 1}. If [[φ]]_M ≠ ∅, define K ∘ φ ={ψ : μ([[ψ]]_M|[[φ]]_M) = 1}; if [[φ]]_M = ∅, define K ∘ φ = Cl(false). Show that this definition of revision satisfies R1–8.

  3. Given a revision operator ∘ satisfying R1–8 (with respect to ⊢ 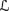and a belief set K ≠ Cl(false), show that there exists a simple conditional probability space M_K = (W, 2^W, 2^W − ∅, μ_K, π) such that (i) K ={ψ : μ([[ψ]]_M) = 1} and (ii) if K ∘ φ ≠ Cl(false), then K ∘ φ ={ψ : μ([[ψ]]_M | [[φ]]_M) = 1}.

  Note that part (b) essentially shows that every conditional probability measure defines a belief revision operator, and part (c) essentially shows that every belief revision operator can be viewed as arising from a conditional probability measure on an appropriate space.

• 9.8 Construct a BCS satisfying REV1 and REV2 that has the properties required in Example 9.3.3. Extend this example to one that satisfies REV1 and REV2 but violates R7 and R8.

• 9.9 Show that if BCS1–3 hold and s_a φ is a local state in 퓙, then 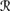[s_a] ∩ 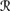[φ]∊′.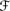

• 9.10 Prove Lemma 9.3.4.

• 9.11 Show that 퓙^†₁ ∊ .

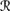
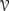• * 9.12 Fill in the missing details of Theorem 9.3.5. In particular, show that the definition of ∘_{s, a} satisfies R1–8 if K ≠ Bel(퓙, s_a) or s_a φ is not a local state in 퓙, and provide the details of the proof that R7 and R8 hold if K = Bel(퓙, s_a) and s_a φ is a local state in 퓙.

• 9.13 Show that the BCS 퓙 constructed in Example 9.3.6 is in .

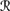
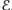
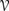• * 9.14 Prove Theorem 9.3.7.

• 9.15 Prove Theorem 9.4.1.

• * 9.16 Complete the proof of Theorem 9.4.2(b) by showing that R7 and R8 hold.

• 9.17 This exercise relates the postulates and property (9.9).

  1. Show that (9.9) follows from R3′, R4′, R7′, and R8′.

  2. Show that if BS satisfies R2′ and ψ ∉ BS(E ∘ φ), then ⊬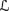_e (φ ∧ ψ).

  3. Describe a system I that satisfies (9.9) and not R9′.

  4. Show that R8′ follows from R2′, R4′ and R9′.

• * 9.18 Complete the proof of Theorem 9.5.1. Moreover, show that (∘, BS_퓙) satisfies R1′–9′, thus proving Theorem 9.5.2.

• * 9.19 Complete the proof of Theorem 9.5.3.

• * 9.20 Complete the proof of Theorem 9.6.2. (The difficulty here, as suggested in the text, is making Pl′ algebraic.)