6.4 The System Clock

Although modern computers are quite fast and getting faster all the time, they still require a finite amount of time to accomplish even the smallest tasks . On von Neumann machines, most operations are serialized , which means that the computer executes commands in a prescribed order. It wouldn't do, in the following code sequence for example, to execute the Pascal statement I := I * 5 + 2 ; before the statement I := J ; finishes:

 I := J;  I := I * 5 + 2;

On real computer systems, operations do not occur instantaneously. Moving a copy of J into I takes a certain amount of time. Likewise, multiplying I by five and then adding two and storing the result back into I takes time. A natural question to ask is, 'How does the processor execute statements in the proper order?' The answer is, 'The system clock.'

The system clock serves as the timing standard within the system, so to understand why certain operations take longer than others, you must first understand the function of the system clock.

The system clock is an electrical signal on the control bus that alternates between zero and one at a periodic rate (see Figure 6-16). All activity within the CPU is synchronized with the edges ( rising or falling) of this clock signal.

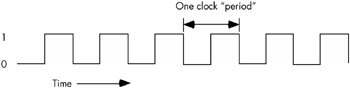
Figure 6-16: The system clock

The frequency with which the system clock alternates between zero and one is the system clock frequency and the time it takes for the system clock to switch from zero to one and back to zero is the clock period. One full period is also called a clock cycle . On most modern systems, the system clock switches between zero and one at rates exceeding several billion times per second. A typical Pentium IV chip, circa 2004, runs at speeds of three billion cycles per second or faster. Hertz (Hz) is the unit corresponding to one cycle per second, so the aforementioned Pentium chip runs at between 3,000 and 4,000 million hertz, or 3,000-4,000 megahertz (MHz), also known as 3-4 gigahertz (GHz). Typical frequencies for 80x86 parts range from 5 MHz up to several gigahertz and beyond.

As you may have noticed, the clock period is the reciprocal of the clock frequency. For example, a 1-MHz clock would have a clock period of one microsecond (one millionth of a second). A CPU running at 1 GHz would have a clock period of one nanosecond (ns), or one billionth of a second. We usually express clock periods in millionths or billionths of a second.

To ensure synchronization, most CPUs start an operation on either the falling edge (when the clock goes from one to zero) or the rising edge (when the clock goes from zero to one). The system clock spends most of its time at either zero or one and very little time switching between the two. Therefore, a clock edge is the perfect synchronization point.

Because all CPU operations are synchronized with the clock, the CPU cannot perform tasks any faster than the clock runs. However, just because a CPU is running at some clock frequency doesn't mean that it executes that many operations each second. Many operations take multiple clock cycles to complete, so the CPU often performs operations at a significantly slower rate.

6.4.1 Memory Access and the System Clock

Memory access is an operation that is synchronized with the system clock. That is, memory access occurs no more often than once every clock cycle. Indeed, on some older processors, it takes several clock cycles to access a memory location. The memory access time is the number of clock cycles between a memory request (read or write) and when the memory operation completes. This is an important value, because longer memory access times result in lower performance.

Modern CPUs are much faster than memory devices, so systems built around these CPUs often use a second clock, the bus clock, which is some fraction of the CPU speed. For example, typical processors in the 100-MHz-to-4-GHz range can use 800-MHz, 500-MHz, 400-MHz, 133-MHz, 100-MHz, or 66-MHz bus clocks (a given CPU generally supports several different bus speeds, and the exact range the CPU supports depends upon that CPU).

When reading from memory, the memory access time is the time between when the CPU places an address on the address bus and the time when the CPU takes the data off the data bus. On typical 80x86 CPUs with a one cycle memory access time, the timing of a read operation looks something like that shown in Figure 6-17. The timing of writing data to memory is similar (see Figure 6-18).

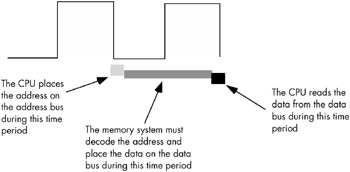
Figure 6-17: A typical memory read cycle

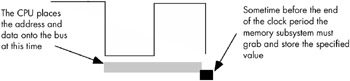
Figure 6-18: A typical memory write cycle

Note that the CPU doesn't wait for memory. The access time is specified by the bus clock frequency. If the memory subsystem doesn't work fast enough to keep up with the CPU's expected access time, the CPU will read garbage data on a memory read operation and will not properly store the data on a memory write. This will surely cause the system to fail.

Memory devices have various ratings, but the two major ones are capacity and speed. Typical dynamic RAM (random access memory) devices have capacities of 512 MB (or more) and speeds of 0.25-100 ns. A typical 3-GHz Pentium system uses 2.0-ns (500-MHz) memory devices.

Wait just a second here! Earlier we saw that the memory speed must match the bus speed or the system would fail. At 3 GHz the clock period is roughly 0.33 ns. How can a system designer get away with using 2.0 ns memory? The answer is wait states.

6.4.2 Wait States

A wait state is an extra clock cycle that gives a device additional time to respond to the CPU. For example, a 100-MHz Pentium system has a 10-ns clock period, implying that you need 10-ns memory. In fact, the implication is that you need even faster memory devices because in most computer systems there is additional decoding and buffering logic between the CPU and memory. This circuitry introduces its own delays. In Figure 6-19, you can see that buffering and decoding costs the system an additional 10 ns. If the CPU needs the data back in 10 ns, the memory must respond in 0 ns (which is impossible ).

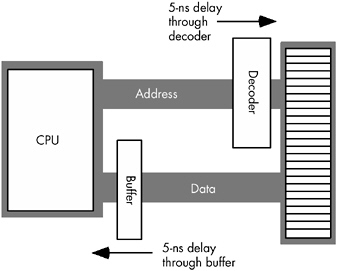
Figure 6-19: Decoding and buffer delays

If cost-effective memory won't work with a fast processor, how do companies manage to sell fast PCs? One part of the answer is the wait state. For example, if you have a 100-MHz processor with a memory cycle time of 10 ns and you lose 2 ns to buffering and decoding, you'll need 8-ns memory. What if your system can only support 20-ns memory, though? By adding wait states to extend the memory cycle to 20 ns, you can solve this problem.

Almost every general-purpose CPU in existence provides a pin (whose signal appears on the control bus) that allows the insertion of wait states. If necessary, the memory address decoding circuitry asserts this signal to give the memory sufficient access time (see Figure 6-20).

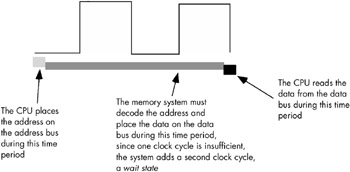
Figure 6-20: Inserting a wait state into a memory read operation

Needless to say, from the system-performance point of view, wait states are not a good thing. While the CPU is waiting for data from memory, it cannot operate on that data. Adding a wait state typically doubles the amount of time required to access memory. Running with a wait state on every memory access is almost like cutting the processor clock frequency in half. You're going to get less work done in the same amount of time.

However, we're not doomed to slow execution because of added wait states. There are several tricks hardware designers can employ to achieve zero wait states most of the time. The most common of these is the use of cache (pronounced 'cash') memory.

6.4.3 Cache Memory

If you look at a typical program, you'll discover that it tends to access the same memory locations repeatedly. Furthermore, you'll also discover that aprogram often accesses adjacent memory locations. The technical names given to these phenomena are temporal locality of reference and spatial locality of reference . When exhibiting spatial locality, a program accesses neighboring memory locations within a short period after the initial memory access.

When displaying temporal locality of reference, a program accesses the same memory location repeatedly during a short time. Both forms of locality occur in the following Pascal code segment:

 for i := 0 to 10 do           A [i] := 0;

There are two occurrences each of spatial and temporal locality of reference within this loop. Let's consider the obvious ones first.

In this Pascal code, the program references the variable i several times. The for loop compares i against 10 to see if the loop is complete. It also increments i by one at the bottom of the loop. The assignment statement also uses i as an array index. This shows temporal locality of reference in action because the CPU accesses i at three points in a short time period.

This program also exhibits spatial locality of reference. The loop itself zeros out the elements of array A by writing a zero to the first location in A , then to the second location in A , and so on. Because Pascal stores the elements of A in consecutive memory locations, each loop iteration accesses adjacent memory locations.

There is an additional example of temporal and spatial locality of reference in this Pascal example. Machine instructions also reside in memory, and the CPU fetches these instructions sequentially from memory and executes these instructions repeatedly, once for each loop iteration.

If you look at the execution profile of a typical program, you'll discover that the program typically executes less than half the statements. Generally, a program might only use 10 to 20 percent of the memory allotted to it. At any one given time, a 1-MB program might only access 4-8 KB of data and code. So if you paid an outrageous sum of money for expensive zero-wait-state RAM, you would only be using a tiny fraction of it at any one given time.Wouldn't it be nice if you could buy a small amount of fast RAM and dynamically reassign its addresses as the program executes?

This is exactly what cache memory does for you. Cache memory sits between the CPU and main memory. It is a small amount of very fast memory. Unlike normal memory, the bytes appearing within a cache do not have fixed addresses. Instead, cache memory can dynamically reassign addresses. This allows the system to keep recently accessed values in the cache. Addresses that the CPU has never accessed or hasn't accessed in sometime remain in main (slow) memory. Because most memory accesses are to recently accessed variables (or to locations near a recently accessed location), the data generally appears in cache memory.

A cache hit occurs whenever the CPU accesses memory and finds the data in the cache. In such a case, the CPU can usually access data with zero wait states. A cache miss occurs if the data cannot be found in the cache. In that case, the CPU has to read the data from main memory, incurring a performance loss. To take advantage of temporal locality of reference, the CPU copies data into the cache whenever it accesses an address not present in the cache. Because it is likely the system will access that same location shortly, the system will save wait states on future accesses by having that data in the cache.

Cache memory does not eliminate the need for wait states. Although a program may spend considerable time executing code in one area of memory, eventually it will call a procedure or wander off to some section of code outside cache memory. When that happens, the CPU has to go to main memory to fetch the data. Because main memory is slow, this will require the insertion of wait states. However, once the CPU accesses the data, it is now available in the cache for future use.

We've discussed how cache memory handles the temporal aspects of memory access, but not the spatial aspects. Caching memory locations when you access them won't speed up the program if you constantly access consecutive locations that you've never before accessed. To solve this problem, when a cache miss occurs most caching systems will read several consecutive bytes of main memory ( engineers call this block of data a cache line ). 80x86 CPUs, for example, read between 16 and 64 bytes upon a cache miss. But this brings up an important question. If you read 16 bytes, why read the bytes in blocks rather than as you need them? As it turns out, most memory chips available today have special modes that let you quickly access several consecutive memory locations on the chip. The cache exploits this capability to reduce the average number of wait states needed to access sequential memory locations. Although reading 16 bytes on each cache miss is expensive if you only access a few bytes in the corresponding cache line, cache memory systems work quite well in the average case.

It should come as no surprise that the ratio of cache hits to misses increases with the size (in bytes) of the cache memory subsystem. The 80486 CPU, for example, has 8,192 bytes of on-chip cache. Intel claims to get an 80-95 percent hit rate with this cache (meaning 80-95 percent of the time the CPU finds the data in the cache). This sounds very impressive. However, if you play around with the numbers a little bit, you'll discover it's not all that impressive. Suppose we pick the 80 percent figure. This means that one out of every five memory accesses, on the average, will not be in the cache. If you have a 50-MHz processor and a 90-ns memory access time, four out of five memory accesses require only one clock cycle (because they are in the cache) and the fifth will require about ten wait states. Ten wait states were computed as follows : five clock cycles to read the first four bytes (10 + 20 + 20 + 20 + 20 = 90). However, the cache always reads 16 consecutive bytes. Most 80486-era memory subsystems let you read consecutive addresses in about 40 ns after accessing the first location. Therefore, the 80486 will require an additional 6 clock cycles to read the remaining three double words. The total is 11 clock cycles or 10 wait states.

Altogether, the system will require 15 clock cycles to access five memory locations, or 3 clock cycles per access, on the average. That's equivalent to two wait states added to every memory access. Doesn't sound so impressive, does it? It gets even worse as you move up to faster processors and the difference in speed between the CPU and memory increases.

There are a couple of ways to improve the situation. First, you can add more cache memory. Alas, you can't pull an 80486 chip apart and solder more cache onto the chip. However, modern Pentium CPUs have a significantly larger cache than the 80486 and operate with fewer average wait states. This improves the cache hit ratio, reducing the number of wait states. For example, increasing the hit ratio from 80 percent to 90 percent lets you access 10 memory locations in 20 cycles. This reduces the average number of wait states per memory access to one wait state, a substantial improvement.

Another way to improve performance is to build a two-level caching system. Many Pentium systems work in this fashion. The first level is the on-chip 8,192-byte cache. The next level, between the on-chip cache and main memory, is a secondary cache often built on the computer system circuit board (see Figure 6-21). However, on newer processors, the first- and second-level caches generally appear in the same packaging as the CPU. This allows the CPU designers to build a higher performance CPU/memory interface, allowing the CPU to move data between caches and the CPU (as well as main memory) much more rapidly .

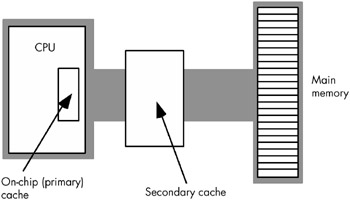
Figure 6-21: A two-level caching system

A typical secondary cache contains anywhere from 32,768 bytes to over 1 MB of memory. Common sizes on PC subsystems are 256 KB, 512 KB, and 1,024 KB (1 MB) of cache.

You might ask, 'Why bother with a two-level cache? Why not use a 262,144-byte cache to begin with?' It turns out that the secondary cache generally does not operate at zero wait states. The circuitry to support 262,144 bytes of fast memory would be very expensive, so most system designers use slower memory, which requires one or two wait states. This is still much faster than main memory. Combined with the existing on-chip level-one cache, you can get better performance from the system with a two-level caching system.

Today, you'll find that some systems incorporate an off-CPU third-level cache . Though the performance improvement afforded by a third-level cache is nowhere near what you get with a first- or second-level cache subsystem, third-level cache subsystems can be quite large (usually several megabytes) and work well for large systems with gigabytes of main memory. For programs that manipulate considerable data, yet exhibit locality of reference, a third-level caching subsystem can be very effective.