15.3 Properties of Subtyping and Typing

< Free Open Study >

Having decided on the definition of the lambda-calculus with subtyping, we now have some work to do to verify that it makes sense—in particular, that the preservation and progress theorems of the simply typed lambda-calculus continue to hold in the presence of subtyping.

15.3.1 Exercise [Recommended, ⋆⋆]

Before reading on, try to predict where difficulties might arise. In particular, suppose we had made a mistake in defining the subtype relation and included a bogus subtyping rule in addition to those above. Which properties of the system can fail? On the other hand, suppose we omit one of the subtyping rules—can any properties then break?

We begin by recording one key property of the subtype relation—an analog of the inversion lemma for the typing relation in the simply typed lambda-calculus (Lemma 9.3.1). If we know that some type S is a subtype of an arrow type, then the subtyping inversion lemma tells us that S itself must be an arrow type; moreover, it tells us that the left-hand sides of the arrows must be (contravariantly) related, and so (covariantly) must the right-hand sides. Similar considerations apply when S is known to be a subtype of a record type: we know that S has more fields (S-RCDWIDTH) in some order (S-RCDPERM), and that the types of common fields are in the subtype relation (S-RCDDEPTH).

15.3.2 Lemma [Inversion of the Subtype Relation]

If S <: T₁ → T₂, then S has the form S₁ → S₂, with T₁ <: S₁ and S₂ <: T₂.
If S <: {l_i:T_i^iÎ1..n}, then S has the form {k_j :S_j^jÎ1..m}, with at least the labels {l_i^iÎ1..n}—i.e., {l_i^iÎ1..n} ⊆ {k_j^jÎ1..m}—and with S_j <: T_i for each common label l_i = k_j.

Proof: EXERCISE [RECOMMENDED, ⋆⋆].

To prove that types are preserved during evaluation, we begin with an inversion lemma for the typing relation (cf. Lemma 9.3.1 for the simply typed lambda-calculus). Rather than stating the lemma in its most general form, we give here just the cases that are actually needed in the proof of the preservation theorem below. (The general form can be read off from the algorithmic subtype relation in the next chapter, Definition 16.2.2.)

15.3.3 Lemma

If Г ⊢ λx:S₁. s₂ : T₁ → T₂, then T₁ <: S₁ and Г, x:S₁ ⊢ S₂ :T₂.
If Г ⊢ {k_a=s_a^aÎ1..m} : {l_i:T_i^iÎ1..n}, then {l_i^iÎ1..n} ⊆ {k_a^aÎ1..m} and Г ⊢ s_a : T_i for each common label k_a = l_i.

Proof: Straightforward induction on typing derivations, using Lemma 15.3.2 for the T-SUB case.

Next, we need a substitution lemma for the typing relation. The statement of this lemma is unchanged from the simply typed lambda-calculus (Lemma 9.3.8), and its proof is nearly identical.

15.3.4 Lemma [Substitution]

If Г, x:S ⊢ t : T and Г ⊢ s : S, then Г ⊢ [x ↦ s]t : T.

Proof: By induction on typing derivations. We need new cases for T-SUB and for the record typing rules T-RCD and T-PROJ, making straightforward use of the induction hypothesis. The rest is just like the proof of 9.3.8.

Now, the preservation theorem has the same statement as before. Its proof, though, is somewhat complicated by subtyping at several points.

15.3.5 Theorem [Preservation]

If Г ⊢ t : T and t → t′, then Г ⊢ t′ : T.

Proof: Straightforward induction on typing derivations. Most of the cases are similar to the proof of preservation for the simply typed lambda-calculus (9.3.9). We need new cases for the record typing rules and for subsumption.

Case T-VAR:

 t = x

Can't happen (there are no evaluation rules for variables).

Case T-ABS:

 t = λx:T₁ .t₂

Can't happen (t is already a value).

Case T-APP:

 t = t₁ t₂    Г ⊢ t₁ : T₁₁→T₁₂    Г ⊢ t₂ : T₁₁     T = T₁₂

From the evaluation rules in Figures 15-1 and 15-2, we see that there are three rules by which t → t′ can be derived: E-App1, E-App2, and E-AppAbs. Proceed by cases.

Subcase E-APP1:

The result follows from the induction hypothesis and T-App.

Subcase E-App2:

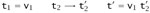
Similar.
Subcase E-APPABS:
t₁ = λx:S₁₁ . t₁₂ t₂ = v₂ t′ = [x ↦ v₂]t₁₂
By Lemma 15.3.3(1), T₁₁ <: S₁₁ and Г,x:S₁₁ ⊢ t₁₂ : T₁₂. By T-SUB, Г ⊢ t₂ : S₁₁. From this and the substitution lemma (15.3.4), we obtain Г ⊢ t′ : T₁₂.

Case T-RCD:

 t = {l_i=t_i ^{iÎ l..n}}     Г ⊢ t_i : T_i   for each i T = {l_i : T_i ^{iÎ l..n}}

The only evaluation rule whose left-hand side is a record is E-RCD. From the premise of this rule, we see that for some field t_j. The result follows from the induction hypothesis (applied to the corresponding assumption Г ⊢ t_j : T_j) and T-RCD.

Case T-PROJ:

 t = t₁ .l_j     Г ⊢ t₁ : {l_i : T_i ^{iÎ l..n}}    T = T_j

From the evaluation rules in Figures 15-1 and 15-2, we see that there are two rules by which t → t′ can be derived: E-PROJ, E-PROJRCD.

Subcase E-PROJ:

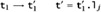
The result follows from the induction hypothesis and T-PROJ.
Subcase E-PROJRCD:
t₁ = {k_a=v_a ^{aÎ l..m}} l_j = k_b t′ = v_b
BY Lemma 15.3.3(2), we have {l_i ^{iÎ l..n}} ⊆ {k_a ^{aÎ l..m}} and Г ⊢ v_a : T_i for each k_a = l_i. In particular, Г ⊢ v_b : T_j, as desired.

Case T-SUB:

 t : S    S <: T

By the induction hypothesis, Г ⊢ t′ : S. By T-SUB, Г ⊢ t : T.

To prove that well-typed terms cannot get stuck, we begin (as in Chapter 9) with a canonical forms lemma, which tells us the possible shapes of values belonging to arrow and record types.

15.3.6 Lemma [Canonical Forms]

If v is a closed value of type T₁ →T₂, then v has the form λx:S₁ .t₂.
If v is a closed value of type {l_i :T _i ^{iÎ l..n}}, then v has the form {k_j =v_j ^{aÎ l..m}}, with {l_i ^{iÎ l..n}} ⊆ {k_a ^{aÎ l..m}}.

Proof: EXERCISE [RECOMMENDED, ⋆⋆⋆].

The progress theorem and its proof are now quite close to what we saw in the simply typed lambda-calculus. Most of the burden of dealing with subtyping has been pushed into the canonical forms lemma, and only a few small changes are needed here.

15.3.7 Theorem [Progress]

If t is a closed, well-typed term, then either t is a value or else there is some t′ with t → t′.

Proof: By straightforward induction on typing derivations. The variable case cannot occur (because t is closed). The case for lambda-abstractions is immediate, since abstractions are values. The remaining cases are more interesting.

Case T-APP:

 t = t₁ t₂     ⊢ t₁ : T₁₁ → T₁₂     ⊢ t₂ :T₁₁    T = T₁₂

By the induction hypothesis, either t₁ is a value or else it can make a step of evaluation; likewise t₂. If t₁ can take a step, then rule E-App1 applies to t. If t₁ is a value and t₂ can take a step, then rule E-App2 applies. Finally, if both t₁ and t₂ are values, then the canonical forms lemma (15.3.6) tells us that t₁ has the form λx:S₁₁ . t₁₂, so rule E-AppAbs applies to t.

Case T-RCD:

 t = {l_i=t_i ^{iÎ l..n}}    for each i Î l..n, ⊢t_i : T_i T = {l_i : T_i ^{iÎ l..n}}

By the induction hypothesis, each t_i either is already a value or can make a step of evaluation. If all of them are values, then t is a value. On the other hand, if at least one can make a step, then rule E-RCD applies to t.

Case T-PROJ:

 t = t₁ . l_j    ⊢ t₁ : {l_i : T_i ^{iÎ l..n}}      T = T_j

By the induction hypothesis, either t₁ is a value or it can make an evaluation step. If t₁ can make a step, then (by E-PROJ) so can t. If t₁ is a value, then by the canonical forms lemma (15.3.6) t₁ has the form {k_a=v_j ^{aÎ l..m}}, with {l_i ^{iÎ l..n}} ⊆ {k_a ^{aÎ l..m}} and with ⊢ v_j : T_i for each l_i = k_j. In particular, l_j is among the labels {k_a ^{aÎ l..m}} of t₁, from which rule E-PROJRCD tells us that t itself can take an evaluation step.

Case T-SUB:

 Г ⊢ t : S      S <: T

The result follows directly from the induction hypothesis.

< Free Open Study >