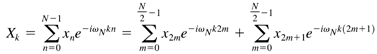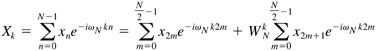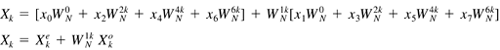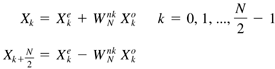Fast Fourier Transform

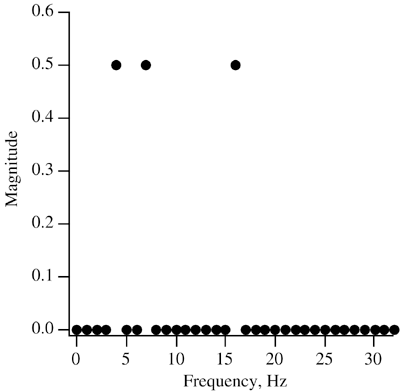
The DFT algorithm is simple to understand. It's easy to program. Everything is wonderful, right? Not exactly. The operation count of the DFT algorithm is proportional to the square of the number of sample points. When we are taking 32 or 64 samples this is not a big deal. However, there are applications of the Fourier transform, such as in the field of seismology, that require millions of data sample points. In this case the efficiency of the DFT algorithm is a big concern.

A number of algorithms have been developed over the years to perform a DFT in a more efficient manner. These algorithms are known as FFT methods . When an FFT performs a transform it requires an operation count proportional to N log ₂ N rather than N ² . For a one million sample analysis the FFT reduces the required operations by a factor of 50,000. There are many variations of FFT algorithms out there today. In this section, we will examine the "standard" radix 2 Decimation in Time (DIT) technique based on the method of Danielson and Lanczos.

FFT methods start with the fact that a DFT can be subdivided into half-size transforms containing the even and odd elements of the original transform.

Equation 22.24

The w _N term in Eq. (22.24) is equal to 2 p / N . If you start with the forward Fourier transform as was done in Eq. (22.24) and split the time domain sequence, it is called DIT. If we had started with the inverse Fourier transform and divided the frequency domain, it would be Decimation in Frequency ( DIF ) . The odd-term summation can be cleaned up a little bit using the following relation.

Equation 22.25

Inserting Eq. (22.25) into Eq. (22.24), we get a form of Eq. (22.24) where the exponential term is the same in both summations.

Equation 22.26

So far, you may be wondering what all the fuss is about. The reason that Eq. (22.26) is significant is that it is only the beginning of the possible transform subdivisions. The two summations on the right-hand side of Eq. (22.26) are themselves DFTs each with half as many points as the original. Indeed, we could rewrite Eq. (22.26) as Eq. (22.27).

Equation 22.27

The DFTs and can themselves be divided into even and odd pieces just as was done by Eq. (22.26). You can continue the decimation process until you are left with a collection of two-point transforms.

This process can probably be best illustrated by the simple example of an eight-point forward Fourier transform. The DFT version of this transform is shown in Eq. (22.28).

Equation 22.28

As before, . The transforms and are themselves divided into even and odd subtransforms.

Equation 22.29

The level terms are defined by the two-point transforms in the brackets of Eq. (22.29). The two-point transforms are relatively easy to compute requiring only a single complex multiplication and a single complex addition.

The process we have just described is actually the reverse of the FFT solution process. The FFT starts at the lowest subdivided transform level, the two-point transforms, and works its way back up, recombining the divided transforms until the full, N -point transform has been recreated. The transform reconstruction algorithm can be done recursively so no additional memory allocation is required for the transformed data. The transform process overwrites the array of input data with the transformed output data. Several other tricks are used to further increase efficiency. The algorithm restricts sine and cosine calls to outer iteration loop and also makes use of the periodic nature of DFTs to evaluate only half of the divided subtransforms by using Eq. (22.30).

Equation 22.30

One caveat about the FFT algorithm that we have described so far is that it depends on dividing a Fourier transform in two. This fact implies that the length of the input data array should also be a multiple of two. If the data set you are using does not have a length equal to a multiple of two, you can simply add zeros to the end of it until its length is the next power of two.

Now it is time to implement an FFT as a Java method. The method is called fastFT() and is declared to be public and static . It is defined in the Fourier class that also defines the discreteFT() method. The first thing the fastFT() method does after declaring and initializing some variables is to rearrange the order of the input data. If you look at Eq. (22.29), you will see that the input data is used in the order [ x , x ₄ , x ₂ , x ₆ , x ₁ , x ₅ , x ₃ , x ₇ ]. It is convenient for the FFT algorithm to place the input data in this type of order before starting the solution process. It turns out the input data can be placed in the proper sequence by reversing the bits of the input data indices. For example, for a system with eight data points, the index number 1 has a binary representation of 001. If you reverse the order of the bits you create the binary number 100, which is equal to the decimal number 4. This tells you to exchange x[1] and x[4] elements in the input data array.

After the bit reversal, the method computes the Fourier transform by recursively building up subtransforms starting with the two-point transforms. The initial data vector is overwritten with the transformed values. If this is a forward transform, the output data is scaled by 1/ N . The fastFT() method source code is shown here.

 public static void fastFT(double[] data, int N,                         boolean forward) {   double omega, tempr, tempi, scale;   double xtemp, cos, sin, xr, xi;   int i, j, k, n, m, M;   //  bit-shift the input data. Remember that N   //  is the number of samples. There is a real and   //  a complex component to each data point.   j=0;   for(i=0; i<N-1; i++) {     if (i<j) {       tempr = data[2*i];       tempi = data[2*i + 1];       data[2*i] = data[2*j];       data[2*i + 1] = data[2*j + 1];       data[2*j] = tempr;       data[2*j + 1] = tempi;     }     k = N/2;     while (k <= j)  {       j -= k;       k >>= 1;     }     j += k;   }   //  Perform the FFT. Recursively build up the   //  full transform from the sub-transforms   if (forward) {     scale = 1.0;   } else {     scale = -1.0;   }   M = 2;   while( M < 2*N ) {     omega = scale*2.0*Math.PI/M;     sin = Math.sin(omega);     cos = Math.cos(omega) - 1.0;     xr = 1.0;     xi = 0.0;     for (m=0; m<M-1; m+=2) {       for (i=m; i<2*N; i+=M*2) {         j = i + M;         tempr = xr*data[j] - xi*data[j+1];         tempi = xr*data[j+1] + xi*data[j];         data[j] = data[i] - tempr;         data[j+1] = data[i+1] - tempi;         data[i] += tempr;         data[i+1] += tempi;       }       xtemp = xr;       xr = xr + xr*cos - xi*sin;       xi = xi + xtemp*sin + xi*cos;     }     M *= 2;   }   //  If this is a forward transform, multiply   //  in the 1/N terms   if ( forward ) {     for(k=0; k<N; ++k) {       data[2*k] /= N;       data[2*k + 1] /= N;     }   }   return; } 

Let's test the fastFT() method by applying it to the composite cosine signal we processed in the "Analyzing Composite Signals" section. The TestFFT.java program sets up and runs this case. The program is very similar to the TestComplex.java program we looked at earlier. The amplitude-time history for a signal containing 4, 7, and 16 Hz components is generated and sent to the fastFT() method. The resulting frequency spectrum is written to the console. The TestFFT class source code follows .

 import TechJava.MathLib.*; public class TestFFT {   public static void main(String args[]) {     int N = 64;     double T = 1.0;     double tn, fk;     double data[] = new double[2*N];     //  A composite cosine function that is sampled     //  for one second at 64 samples/sec     for(int i=0; i<N; ++i) {       data[2*i] = Math.cos(8.0*Math.PI*i*T/N) +                   Math.cos(14.0*Math.PI*i*T/N) +                   Math.cos(32.0*Math.PI*i*T/N);       data[2*i+1] = 0.0;     }     //  Compute the Fourier Transform     Fourier.fastFT(data, N, true);     //  Print out the frequency spectrum     System.out.println();     for(int k=0; k<N; ++k) {       fk = k/T;       System.out.println("f["+k+"] = " + fk +                        "  Xr["+k+"] = " + data[2*k] +                        "  Xi["+k+"] = " + data[2*k+1]);     }   } } 

The results for this test case are shown in Figure 22.7. The fastFFT() method correctly computed the frequency spectrum with peaks at the 4, 7, and 16 Hz frequencies. Just to get a feeling for the efficiency difference between DFT and FFT, this case was rerun through the discreteFT() and fastFT() methods using 131072 (2 ¹⁷ ) samples. On a 1.6 GHz Pentium 4 PC, the fastFT() method took about one second to execute. The discreteFT() method, on the other hand, required over 2 hours to perform the same calculation.

Figure 22.7. FFT results for composite cosine signa