Selective Greed

So far, except for our preview of overloaded scheduling and our use of speculation, the best strategy has smacked of a “follow your nose” (also known as greedy) approach:

If a move lowers the cost/gets closer to the solution, take it; otherwise, avoid it.

Sometimes that basic philosophy works but requires a slight modification:

Find the lowest cost solutions to subproblems, and then glue the solutions to the best subproblems together.

Welcome to dynamic programming. This is a technique with an enormous number of applications. We’ll start with string editing, but soon you’ll be planning menus.

The string edit problem is to convert a source string to a target string in the fewest number of “edits” possible. There are three kinds of edits: changing a letter (e.g., ‘a’ becomes ‘b’), inserting a letter (e.g., replace a blank by ‘c’), and deleting a letter (e.g., replacing ‘c’ by a blank). For example, to edit the word ‘rent’ to the semantically equivalent (if you live in the United Kingdom) ‘let’, we would change ‘r’ to ‘l’ and delete ‘n’. To go the other way, we would change ‘l’ to ‘r’ and insert ‘n’. The other letters don’t change. Either way, the edit distance is 2.

Warm-Up

When the words are short, it is easy to find an answer by eye, but consider this example inspired by genomics.

How many edits are needed to convert ‘TAGATGGTCT’ to ‘TGGAGACAGTCT’? Go ahead and give it a try.

Solution to Warm-Up

To understand the dynamic programming approach to this problem, consider a small conversion example: ‘AGA’ to ‘TGGAG’. For the moment, resist the temptation to do this by eye and take a look at the matrix in Figure 2-7.

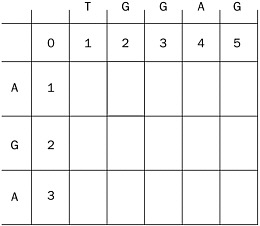
Figure 2-7: The beginning of the dynamic programming matrix. The top row represents the number of inserts to go from an empty string to, respectively, an empty string, a string consisting of ‘T’ alone, a string consisting of ‘TG’, and so on. The left column represents the number of deletes to go to an empty string from, respectively, an empty string, a string consisting of ‘A’, a string consisting of ‘AG’, and a string consisting of ‘AGA’.

We’ve written ‘TGGAG’ above the matrix and ‘AGA’ to the left of the matrix. The number in the top row of the matrix corresponds to the number of inserts, in turn, required to go from the empty string to the empty string (0), from the empty string to ‘T’ (1), from the empty string to ‘TG’ (2), and so on up to 5. The leftmost column corresponds to the number of deletes to go, in turn, from the empty string to the empty string (0), from ‘A’ to the empty string (1), and so on. That ends the setup phase.

Now we will fill in the matrix row by row. Location (0, 0), that is row 0, column 0, is the top left corner. Row i, column j will correspond to the edit distance between letters 1 through i of ‘AGA’ and 1 through j of ‘TGGAG’. As we fill in the entry for row i, column j, we will already have filled in entries for row i-1, column j (the entry above), row i, column j-1 (the entry to the left), and row i-1, column j-1 (the entry that is the upper left diagonal). We will use those values as well as the i^th letter of ‘AGA’ and the j^th letter of ‘TGGAG’ to determine the entry for row i, column j.

In the following formula, differs(i,j) will be 1 if the i^th letter of ‘AGA’ differs from the j^th letter of ‘TGGAG’ and 0 otherwise.

 entry(row i, column j) = min(entry(row i-1, column j) + 1,   entry(row i, column j-1) + 1,   entry(row i-1, column j-1) + differs(i,j))

Look at the entry under the T and in the row of the first A in Figure 2-8.

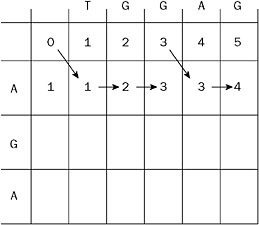
Figure 2-8: Filling in the second row corresponds to the problem of transforming ‘A’ to ‘TGGAG’. As you can see from the arrows, the best thing to do is to insert ‘TGG’ and then ‘G’ along with a zero-cost replacement of ‘A’ by ‘A’.

The arrow indicates that the value in that square comes from the upper left diagonal neighbor, because 0 + differs(1,1) = 0 + 1 = 1 is less than what could have been obtained from coming from the left (1 + 1 = 2) or from above (1 + 1 = 2). So, in this case, the cheapest way to edit from ‘A’ to ‘T’ is to replace ‘A’ by ‘T’. The alternative coming from the left would be: Delete ‘A’ and then insert ‘T’ for a cost of 2. The alternative from the top would be: Insert ‘T’ and then delete ‘A’. The entry under the first G could come either from its upper left diagonal neighbor or from the left. The way we’ve drawn it, the path until this point says “to go from A to TG, replace A by T and insert G.” This corresponds to an edit distance of 2.

Now go two to the right (to the entry under the A). In this case, the cheapest path is from the upper left diagonal which has a value 3. Note that differ(1,4) = 0, because the first character of ‘AGA’ and the fourth character of ‘TGGAG’ are both ‘A’. This corresponds to inserting ‘T’, ‘G’, ‘G’ (at a cost of 3) and then replacing ‘A’ by ‘A’ (at a cost of 0). The last entry is at a cost of 4, because it corresponds to the above steps followed by the insertion of ‘G’. The point is that each square is filled in by looking at just its three neighbors: left, up, and upper left.

Now we are ready for the next row. In Figure 2-9, notice that the entry to the right of the G in ‘AGA’ and beneath the first G in ‘TGGAG’ is 1 and it is less than its neighbors to the left and above. That entry corresponds to replacing ‘A’ by ‘T’ and ‘G’ by ‘G’. The rightmost entry of that G row corresponds to inserting ‘T’, ‘G’, and ‘G’, and then replacing the ‘A’ by ‘A’ and the ‘G’ by ‘G’.

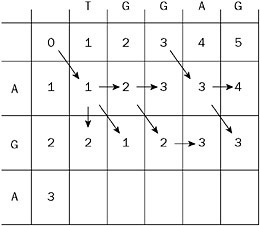
Figure 2-9: Filling in the third row of the dynamic programming matrix plus indications of some possible best paths, though not all of them.

By now, you should understand the idea well enough to be able to trace the path for the full solution, as shown in Figure 2-10.

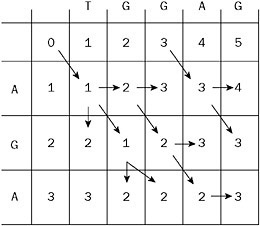
Figure 2-10: The entire matrix for the warm-up. In the end, we match ‘GA’ with ‘GA’ and insert or relabel for the rest.

The path to the lower right corresponds to replace ‘A’ by ‘T’, insert ‘G’, replace ‘G’ by ‘G’, replace ‘A’ by ‘A’ and insert ‘G’. This gives an optimal cost of 3. There is one other optimal editing pattern: Replace ‘A’ by ‘T’, replace ‘G’ by ‘G’, insert ‘G’, replace ‘A’ by ‘A’, and insert ‘G’.

Dynamic programming is a greedy method in that you fill in every square based on local cost considerations. We call it selective greed because you explore many subproblems before combining the best of them to arrive at the optimal. It’s a good metaphor for research.

Now it’s your turn. You want to convert ‘TAGATGGTCT’ to ‘TGGAGACAGTCT’. To get you started, I’ve given you the outline in Figure 2-11.

Figure 2-11: Fill in this matrix to solve the problem.

1. See if you can find the edit distance between the two strings by filling in the figure. While you’re at it, count the different ways of converting ‘TAGATGGTCT’ to ‘TGGAGACAGTCT’.

Solution to Selective Greed

1. See if you can find the edit distance between the two strings by filling in the figure. While you’re at it, count the different ways of converting “TAGATGGTCT” to “TGGAGACAGTCT”.

Replace ‘T’ by ‘T’, insert ‘G’, insert ‘G’, replace ‘A’ by ‘A’, replace ‘G’ by ‘G’, replace ‘A’ by ‘A’, replace ‘T’ by ‘C’, replace ‘G’ by ‘A’, and then replace “GTCT” by “GTCT”. This gives a total cost of 4, as shown in Figure 2-12.

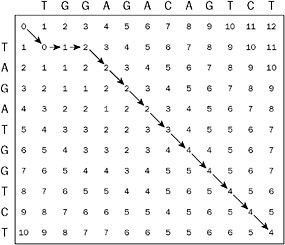
Figure 2-12: An optimal edit sequence to go from “TAGATGGTCT” to “TGGAGACAGTCT”. Starting from the first letter, there are many replacements. Arrows always point to the right, downward, or to the right and downward.