3.2 Arrays
Perhaps the most fundamental data structure is the array, which is defined as a primitive in Java and in most other programming languages. We have already seen, in the examples in Chapter 1, the use of an array as the basis for the development of an efficient algorithm; we shall see many more examples in this section.
An array is a fixed collection of same-type data that are stored contiguously and are accessible by an index. We refer to the ith element of an array a as a[i]. It is the responsibility of the programmer to store something meaningful in an array position a[i] before referring to a[i]. In Java, it is also the responsibility of the programmer to use indices that are nonnegative and smaller than the array size. Neglecting these responsibilities are two of the more common programming mistakes.
Arrays are fundamental data structures in that they have a direct correspondence with memory systems on virtually all computers. To retrieve the contents of a word from memory in machine language, we provide an address. Thus, we could think of the entire computer memory as an array, with the memory addresses corresponding to array indices. Most computer-language processors translate programs that involve arrays into efficient code that directly accesses memory, and we are safe in assuming that an array access such as a[i] translates to just a few machine instructions.
Program 3.4 Sieve of Eratosthenes
The goal of this program is to print all the primes less than the integer given as a command-line argument. To do so, it computes an array of boolean values with a[i] set to true if i is prime, and to false if i is not prime. First, it sets to true all array elements in order to indicate that no numbers are known to be nonprime. Then it sets to false array elements corresponding to indices that are known to be nonprime (multiples of known primes). If a[i] is still true after all multiples of smaller primes have been set to false, then we know it to be prime.
class Primes { public static void main(String[] args) { int N = Integer.parseInt(args[0]); boolean[] a = new boolean[N]; for (int i = 2; i < N; i++) a[i] = true; for (int i = 2; i < N; i++) if (a[i] != false) for (int j = i; j*i < N; j++) a[i*j] = false; for (int i = 2; i < N; i++) if (i > N - 100) if (a[i]) Out.print(" " + i); Out.println(); } } A simple example of the use of an array is given by Program 3.4, which prints out all prime numbers less than a specified value. The method used, which dates back to the third century B.C., is called the sieve of Eratosthenes. It is typical of algorithms that exploit the fact that we can access efficiently any item of an array, given that item's index. Figure 3.2 traces the operation of the program when computing the primes less than 32. For economy, we use the numbers 1 and 0 in the figure to denote the values true and false, respectively.
Figure 3.2. Sieve of Eratosthenes
To compute the prime numbers less than 32, we initialize all the array entries to 1 (second column) in order to indicate that no numbers are known to be nonprime (a[0] and a[1] are not used and are not shown). Then, we set array entries whose indices are multiples of 2, 3, and 5 to 0, since we know these multiples to be nonprime. Indices corresponding to array entries that remain 1 are prime (rightmost column).
Program 3.5 Robust array allocation
If a user of Program 3.4 types a huge number as command-line argument, it will throw an OutOfMemoryError exception. It is good programming practice to check for all errors that might occur, so we should replace the line that creates the boolean array a in Program 3.4 with this code. We frequently allocate arrays in code in this book, but, for brevity, we will omit these insufficient-memory tests.
boolean[] a; try { a = new boolean[N]; } catch (OutOfMemoryError e) { Out.println("Out of memory"); return; } The implementation has four loops, three of which access the items of the array sequentially, from beginning to end; the fourth skips through the array, i items at a time. In some cases, sequential processing is essential; in other cases, sequential ordering is used because it is as good as any other. For example, we could change the first loop in Program 3.4 to
for (i = N-1; i > 1; i--) a[i] = true;
without any effect on the computation. We could also reverse the order of the inner loop in a similar manner, or we could change the final loop to print out the primes in decreasing order, but we could not change the order of the outer loop in the main computation, because it depends on all the integers less than i being processed before a[i] is tested for being prime.
We will not analyze the running time of Program 3.4 in detail because that would take us astray into number theory, but it is clear that the running time is proportional to
which is less than N + N/2 + N/3 + N/4 + ... = NHN ~ N ln N.
As with other objects, references to arrays are significant because they allow us to manipulate the arrays efficiently as higher-level objects. In particular, we can pass a reference to an array as an parameter to a method, thus enabling that method to access objects in the array without having to make a copy of the whole array. This capability is indispensable when we write programs to manipulate huge arrays. For example, the search methods that we examined in Section 2.6 use this feature. We shall see other examples in Section 3.7.
The second basic mechanism that we use in Program 3.4 is the new operator that allocates the amount of memory that we need for our array at execution time and returns, for our exclusive use, a reference to the array. Dynamic allocation is an essential tool in programs that manipulate multiple arrays, some of which might have to be huge. In this case, without memory allocation, we would have to predeclare an array as large as any value that the user is allowed to type. In a large program where we might use many arrays, it is not feasible to do so for each array. For Java, the underlying mechanism new is the same as for any other object, but its use is particularly important for arrays, which could be huge. A robust version of Program 3.4 would also check that there is sufficient memory available for the array, as illustrated in Program 3.5.
Not only do arrays closely reflect the low-level mechanisms for accessing data in memory on most computers, but also they find widespread use because they correspond directly to natural methods of organizing data for applications. For example, arrays also correspond directly to vectors, the mathematical term for indexed lists of objects.
The Java standard library provides the class Vector, an abstract object that we can index like an array but that can also grow and shrink. We get some of the benefit of arrays but can work with abstract operations for making an array larger or smaller without having to worry about the details of coding them. Programs that use Vector objects are more cumbersome than programs that use arrays, because to access the ith element of a Vector we have to call its get method instead of using square braces. The implementation of Vector most likely uses an internal array, so using a Vector instead of an array just leads to an extra level of indirection for most references. Therefore, for simplicity and efficiency, we use arrays in all of our code while recognizing that it could be adapted to use Vectors if desired (see Exercise 3.15).
Program 3.6 is an example of a simulation program that uses an array. It simulates a sequence of Bernoulli trials, a familiar abstract concept from probability theory. If we flip a coin N times, the
Program 3.6 Coin-flipping simulation
If we flip a coin N times, we expect to get N/2 heads, but could get anywhere from 0 to N heads. This program runs the experiment M times, taking both N and M from the command line. It uses an array f to keep track of the frequency of occurrence of the outcome "i heads" for 0 
i N, then prints out a histogram of the result of the experiments, with one asterisk for each 10 occurrences. The operation on which this program is based indexing an array with a computed value is critical to the efficiency of many computational procedures.
class CoinFlip { static boolean heads() { return Math.random() < 0.5; } public static void main(String[] args) { int i, j, cnt; int N = Integer.parseInt(args[0]); int M = Integer.parseInt(args[1]); int[] f = new int[N+1]; for (j = 0; j <= N; j++) f[j] = 0; for (i = 0; i < M; i++, f[cnt]++) for (cnt = 0, j = 0; j <= N; j++) if (heads()) cnt++; for (j = 0; j <= N; j++) { if (f[j] == 0) Out.print("."); for (i = 0; i < f[j]; i+=10) Out.print("*"); Out.println(); } } } probability that we see k heads is
The approximation is known as the normal approximation the familiar bell-shaped curve. Figure 3.3 illustrates the output of Program 3.6 for 1000 trials of the experiment of flipping a coin 32 times. Many more details on the Bernoulli distribution and the normal approximation can be found in any text on probability. In the present context, our interest in the computation is that we use the numbers as indices into an array to count their frequency of occurrence. The ability of arrays to support this kind of operation is one of their prime virtues.
Figure 3.3. Coin-flipping simulation
This table shows the result of running Program 3.6 with N = 32 and M = 1000, simulating 1000 experiments of flipping a coin 32 times. The number of heads that we should see is approximated by the normal distribution function, which is drawn over the data.
Programs 3.4 and 3.6 both compute array indices from the data at hand. In a sense, when we use a computed value to access an array of size N, we are taking N possibilities into account with just a single operation. This gain in efficiency is compelling when we can realize it, and we shall be encountering algorithms throughout the book that make use of arrays in this way.
We use arrays to organize all different manner of types of objects, not just integers. In Java, we can declare arrays of any primitive or class type. An array of integers contains the values of the integers themselves, and the same is true of any other primitive type. But an array of objects is an array of references to the objects, as depicted in Figure 3.4.
Figure 3.4. Array of points
An array of objects in Java is actually an array of references to the objects, as depicted in this diagram of an array of Point objects.
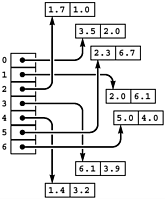
Program 3.7 illustrates the use of an array of points in the plane using the class definition for points that we considered in Section 3.1. This program also illustrates a common use of arrays: to save data away so that they can be quickly accessed in an organized manner in some computation.
Incidentally, Program 3.7 is also interesting as a prototypical quadratic algorithm, which checks all pairs of a set of N data items, and therefore takes time proportional to N2. In this book, we look for improvements whenever we see such an algorithm, because its use becomes infeasible as N grows. In this case, we shall see how to use a compound data structure to perform this computation in linear time, in Section 3.7.
We can create compound types of arbitrary complexity in a similar manner: We can have not just arrays of objects, but also arrays of arrays, or objects containing arrays. We will consider these different options in detail in Section 3.7. Before doing so, however, we will examine linked lists, which serve as the primary alternative to arrays for organizing collections of objects.
Program 3.7 Closest-point computation
This program illustrates the use of an array of objects and is representative of the typical situation where we save items in an array to process them later, during some computation. It counts the number of pairs of N randomly generated points in the unit square that can be connected by a straight line of length less than d, using the data type for points described in Section 3.1. The running time is O(N2), so this program cannot be used for huge N. Program 3.18 provides a faster solution.
class ClosePoints { public static void main(String[] args) { int cnt = 0, N = Integer.parseInt(args[0]); double d = Double.parseDouble(args[1]); Point[] a = new Point[N]; for (int i = 0; i < N; i++) a[i] = new Point(); for (int i = 0; i < N; i++) for (int j = i+1; j < N; j++) if (a[i].distance(a[j]) < d) cnt++; Out.print(cnt + " pairs "); Out.println("closer than " + d); } } Exercises
3.12 Modify our implementation of the sieve of Eratosthenes (Program 3.4) to use an array of ints; instead of booleans. Determine the effects of these changes on the amount of space and time used by the program.
3.13 Use the sieve of Eratosthenes to determine the number of primes less than N, for N = 103, 104, 105, and 106.
N versus the number of primes less than N for N between 1 and 1000.
3.16 Empirically determine the effect of removing the test of a[i] from the inner loop of Program 3.4, for N = 103, 104, 105, and 106, and explain the effect that you observe.
for (i = 0; i < 99; i++) a[i] = 98-i; for (i = 0; i < 99; i++) a[i] = a[a[i]];
3.22 Modify Program 3.6 to simulate a situation where the coin turns up heads with probability l/N. Run 1000 trials for an experiment with 32 flips to get output that you can compare with Figure 3.3. This distribution is the classical Poisson distribution.
| Top |
EAN: 2147483647
Pages: 158