Chapter 17: Do It Yourself: Test LINT | Cryptography in C and C++

Team-Fly

90% of the time is spent in 10% of the code.

—Robert Sedgewick, Algorithms

WE HAVE ALREADY DISCUSSED THE topic of testing in Chapter 12, where we subjected the basic arithmetic functions of the first part of the book to extensive static and dynamic tests. We now require a similar treatment for the validation of the C++ class LINT, and furthermore, we still must provide tests of the number-theoretic C functions.

The approach of the static tests can be carried over directly to the LINT class, where the tool PC-lint (see [Gimp]) used for the static analysis of C functions will stand us here in good stead as well, since we can use it for checking the syntactic correctness and (within certain bounds) the semantic plausibility of the LINT class and its elements.

We are also interested in the functional aspects of our class implementation: We must demonstrate that the methods contained in LINT return correct results. The process that we used earlier, where the results of equivalent or mutually inverse operations were used to establish correctness, can also, of course, be used on C++ functions. In the following example this process is embodied in the function testdist(), which links addition and multiplication by way of the distributive law. Even here one can see how much less syntactic complication is needed in comparison with the test functions in C. The test function consists principally of two lines of code!

   #include <stdio.h>   #include <stdlib.h>   #include "flintpp.h"   void report_error (LINT&, LINT&, LINT&, int);   void testdist (int);   #define MAXTESTLEN CLINTMAXBIT   #define CLINTRNDLN (ulrand64_l()% (MAXTESTLEN + 1))   main()   {     testdist (1000000);   }   void testdist (int nooftests)   {     LINT a;     LINT b;     LINT c;     int i;     for (i = 1; i < nooftests; i++)       {          a = randl (CLINTRNDLN);          b = randl (CLINTRNDLN);          c = randl (CLINTRNDLN);          // test of + and * by application of the distributive law          if ((a + b)*c != (a*c + b*c))            report_error (a, b, c, __LINE__);       }   }   void report_error (LINT& a, LINT& b, LINT& c, int line)   {     LINT d = (a + b) * c;     LINT e = a * c + b * c;     cerr << "error in distributive law before line " << line << endl;     cerr << "a = " << a << endl;     cerr << "b = " << b << endl;     cerr << "(a + b) * c = " << d << endl;     cerr << "a * c + b * c = " << e << endl;     abort();   }

We now leave it to the reader as an exercise to test all the LINT operators in this or a similar manner. For orientation, one may look at the test routines for the C functions. However, there are some new aspects to consider, such as the prefix and postfix operators ++ and −−, as well as the fact that == is also an operator that must be tested. Here are some additional program notes:

Tests of the error routine panic() with all defined errors, with and without exceptions;
Tests of the I/O functions, stream operators, and manipulators;
Tests of the arithmetic and number-theoretic functions.

The number-theoretic functions can be tested according to the same principles as the arithmetic functions. To examine the function to be tested one is well advised to use inverse functions, equivalent functions, or different implementations of the same function that are as independent as possible from one another. We have examples of each of these variants:

If the Jacobi symbol indicates that an element of a finite ring is a square, this can be verified by calculating the square root. Conversely, a calculated square root can be verified as such by a simple modular squaring.
The function inv() for calculating the multiplicative inverse i of an integer a modulo n can be tested with the condition ai ≡ 1 mod n.
For calculating the greatest common divisor of two integers one may make use of the two FLINT/C functions gcd_l() and xgcd_l(), where the latter returns the representation of the greatest common divisor as a linear combination of the arguments. The results can be compared one with the other, and the linear combination can be constructed, which in turn must agree with the greatest common divisor.
Redundance is also to be found in the relation between the greatest common divisor and the least common multiple: For integers a, b one has the relation

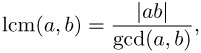
a fruitful relation that can also easily be checked. Additional useful formulas that relate the greatest common divisor and least common multiple are presented in Section 10.1.
Finally, for testing the primality test the RSA procedure can be invoked: If p or q is not prime, then with high probability φ(n) ≠ (p − 1)(q − 1), so that the RSA algorithm will not function correctly. This can be recognized in that a key pair modulo pq does not make possible the requisite mutually inverse RSA operations.

There are thus sufficiently many and varied approaches to effective testing of the LINT functions. The reader is encouraged to develop and implement at least one such test for each LINT function. It is highly effective both as a test and as an exercise and will develop in the user of the LINT class familiarity with how the class works and the uses to which it might be put.

Team-Fly