10.1 Greatest Common Divisor

Team-Fly

That schoolchildren are taught to use the method of prime factorization rather than the more natural method of the Euclidean algorithm to compute the greatest common divisor of two integers is a disgrace to our system of education.

—W. Heise, P. Quattrocci, Information and Coding Theory

Stated in words, the greatest common divisor (gcd) of integers a and b is the positive divisor of a and b that is divisible by all common divisors of a and b. The greatest common divisor is thereby uniquely determined. In mathematical notation the greatest common divisor d of two integers a and b, not both zero, is defined as follows: d = gcd(a, b) if d > 0, d | a, d | b, and if for some integer d′ we have d′ | a and d′ | b, then we also have d′ | d.

It is convenient to extend the definition to include

The greatest common divisor is thus defined for all pairs of integers, and in particular for the range of integers that can be represented by CLINT objects. The following rules hold:

(10.1)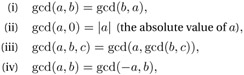

of which, however, only (i)–(iii) are relevant for CLINT objects.

It is obligatory first to consider the classical procedure for calculating the greatest common divisor according to the Greek mathematician Euclid (third century B.C.E.), which Knuth respectfully calls the grandfather of all algorithms (definitely see [Knut], pages 316 ff.). The Euclidean algorithm consists in a sequence of divisions with remainder, beginning with the reduction of a mod b, then b mod (a mod b), and so on until the remainder vanishes.

Euclidean algorithm for calculating gcd(a, b) for a, b ≥ 0

If b = 0, output a and terminate the algorithm.
Set r ← a mod b, a ← b, b ← r, and go to step 1.

For natural numbers a₁, a₂ the calculation of the greatest common divisor according to the Euclidean algorithm goes as follows:

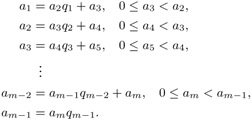
click to expand

Result:

We compute as an example gcd(723, 288):

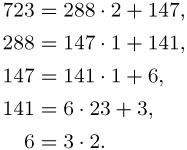
Result:

This procedure works very well for calculating the greatest common divisor or for letting a computer program do the work. The corresponding program is short, quick, and, due to its brevity, provides few opportunities for error.

A consideration of the following properties of integers and of the greatest common divisor indicates—at least theoretically—possibilities for improvement for programming this procedure:

(10.2)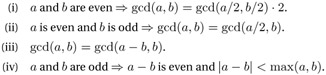

The advantage of the following algorithm based on these properties is that it uses only size comparisons, subtractions, and shifts of CLINT objects, operations that do not require a great deal of computational time and for which we use efficient functions; above all, we need no divisions. The binary Euclidean algorithm for calculating the greatest common divisor can be found in almost the identical form in [Knut], Section 4.5.2, Algorithm B, and in [Cohe], Section 1.3, Algorithm 1.3.5.

Binary Euclidean algorithm for calculating gcd(a, b) for a, b ≥ 0

If a < b, exchange the values of a and b. If b = 0, output a and terminate the algorithm. Otherwise, set k ← 0, and as long as a and b are both even, set k ← k + 1, a ← a/2, b ← b/2. (We have exhausted property (i); a and b are now no longer both even.)
As long as a is even, set repeatedly a ← a/2 until a is odd. Or else, if b is even, set repeatedly b ← b/2 until b is odd. (We have exhausted property (ii); a and b are now both odd.)
Set t ← (a − b)/2. If t = 0, output 2^k a and terminate the algorithm. (We have used up properties (ii), (iii), and (iv).)
As long as t is even, set repeatedly t ← t/2, until t is odd. If t > 0, set a ← t; otherwise, set b ← −t; and go to step 3.

This algorithm can be translated step for step into a programmed function, where we take the suggestion from [Cohe] to execute in step 1 an additional division with remainder and set r ← a mod b, a ← b, and b ← r. We thereby equalize any size differences between the operands a and b that could have an adverse effect on the running time.

Function:	greatest common divisor
Syntax:	void gcd_l (CLINT aa_l, CLINT bb_l, CLINT cc_l);
Input:	aa_l, bb_l (operands)
Output:	cc_l (greatest common divisor)

 void gcd_l (CLINT aa_l, CLINT bb_l, CLINT cc_l) {   CLINT a_l, b_l, r_l, t_l;   unsigned int k = 0;   int sign_of_t;

Step 1: If the arguments are unequal, the smaller argument is copied to b_l. If b_l is equal to 0, then a_l is output as the greatest common divisor.

   if (LT_L (aa_l, bb_l))     {       cpy_l (a_l, bb_l);       cpy_l (b_l, aa_l);     }   else     {       cpy_l (a_l, aa_l);       cpy_l (b_l, bb_l);     }   if (EQZ_L (b_l))     {       cpy_l (cc_l, a_l);       return;     }

The following division with remainder serves to scale the larger operand a_l. Then the powers of two are removed from a_1 and b_1.

   (void) div_l (a_l, b_l, t_l, r_l);   cpy_l (a_l, b_l);   cpy_l (b_l, r_l);   if (EQZ_L (b_l))     {       cpy_l (cc_l, a_l);       return;     }   while (ISEVEN_L (a_l) && ISEVEN_L (b_l))     {       ++k;       shr_l (a_l);       shr_l (b_l);     }

Step 2.

   while (ISEVEN_L (a_l))     {       shr_l (a_l);     }   while (ISEVEN_L (b_l))     {       shr_l (b_l);     }

Step 3: Here we have the case that the difference of a_l and b_l can be negative. This situation is caught by a comparison between a_l and b_l. The absolute value of the difference is stored in t_l, and the sign of the difference is stored in the integer variable sign_of_t. If t_l == 0. Then the algorithm is terminated.

   do     {       if (GE_L (a_l, b_l))          {            sub_l (a_l, b_l, t_l);            sign_of_t = 1;          }       else          {            sub_l (b_l, a_l, t_l);            sign_of_t = −1;          }       if (EQZ_L (t_l))          {            cpy_l (cc_l, a_l);     /* cc_l <- a */            shift_l (cc_l, (long int) k);    /* cc_l <- cc_l*2**k */            return;          }

Step 4: Depending on the sign of t_l, we have t_l allocated to a_l or b_l.

       while (ISEVEN_L (t_l))          {            shr_l (t_l);          }       if (−1 == sign_of_t)          {            cpy_l (b_l, t_l);          }       else          {            cpy_l (a_l, t_l);          }     }   while (1); }

Although the operations used are all linear in the number of digits of the operands, tests show that the simple two-line greatest common divisor on page 166 is hardly slower as a FLINT/C function than this variant. Somewhat surprised at this, we ascribe this situation, for lack of better explanation, to the efficiency of our division routine, as well as to the fact that the latter version of the algorithm requires a somewhat more complex structure.

The calculation of the greatest common divisor for more than two arguments can be carried out with multiple applications of the function gcd_l(), since as we showed above in (10.1)(iii) the general case can be reduced recursively to the case with two arguments:

(10.3)

With the help of the greatest common divisor it is easy to determine the least common multiple (lcm) of two CLINT objects a_l and b_l. The least common multiple of integers n₁,...,n_r, all nonzero, is defined as the smallest element of the set { m Î | n_i divides m, i = 1,...,r}. Since it contains at least the product |n_i|, this set is nonempty. For two arguments a, b Î the least common multiple can be computed as the absolute value of their product divided by the greatest common divisor:

(10.4)

We shall use this relation for the calculation of the least common multiple of a_l and b_l.

Function:	least common multiple (lcm)
Syntax:	int lcm_l (CLINT a_l, CLINT b_l, CLINT c_l);
Input:	a_l, b_l (operands)
Output:	c_l (lcm)
Return:	E_CLINT_OK if all ok E_CLINT_OFL if overflow

 int lcm_l (CLINT a_l, CLINT b_l, CLINT c_l) {   CLINT g_l, junk_l;   if (EQZ_L (a_l) || EQZ_L (b_l))     {       SETZERO_L (c_l);       return E_CLINT_OK;     }   gcd_l (a_l, b_l, g_l);   div_l (a_l, g_l, g_l, junk_l);   return (mul_l (g_l, b_l, c_l)); }

It holds for the least common multiple as well that its calculation for more than two arguments can be recursively reduced to the case of two arguments:

(10.5)

Formula (10.4) above does not, however, hold for more than two numbers: The simple fact that lcm(2, 2, 2) · gcd(2, 2, 2) = 4 ≠ 2³ can serve as a counterexample. There does exist, however, a generalization of this relation between the greatest common divisor and the least common multiple for more than two arguments. Namely, we have

(10.6)

and also

(10.7)

The special relationship between the greatest common divisor and the least common multiple is expressed in additional interesting formulas, demonstrating an underlying duality, in the sense that exchanging the roles of greatest common divisor and least common multiple does not affect the validity of the formula, just as in (10.6) and (10.7). We have the distributive law for gcd and lcm, namely,

(10.8)

(10.9)

and to top it all off we have (see [Schr], Section 2.4)

(10.10)

Aside from the obvious beauty of these formulas on account of their fearful symmetry, they also serve to provide excellent tests for functions that deal with greatest common divisor and least common multiple, where the arithmetic functions used are implicitly tested as well (on the subject of testing, see Chapter 12).

Don't blame testers for finding your bugs.

—Steve Maguire

Team-Fly