4.3 Division with Remainder

Team-Fly

---

4.3 Division with Remainder

And marriage and death and division

Make barren our lives.

—Algernon Charles Swinburne, "Dolores"

We still need to place the last stone in our edifice of the fundamental arithmetic processes on large numbers, namely, division, which is the most complex of them all. Since we are calculating with natural numbers, we have only natural numbers at our disposal to express the results of a division. The principle of division that we are about to expound will be called division with remainder. It is based on the following relation. Given a, b Î , b > 0, there are unique integers q and r that satisfy a = qb + r with 0 ≤ r < b. We call q the quotient and r the remainder of the division of a by b.

Frequently, we are interested only in the remainder and couldn't care less about the quotient. In Chapter 5 we shall see the importance of the operation of calculating remainders, since it is used in many algorithms, always in conjunction with addition, subtraction, multiplication, and exponentiation. Thus it will be worth our while to have at our disposal as efficient a division algorithm as possible.

For natural numbers a and b the simplest way of executing a division with remainder consists in subtracting the divisor b from the dividend a continually until the remaining quantity r is smaller than the divisor. By counting how often we have carried out the subtraction we will have calculated the quotient. The quotient q and the remainder r have the values q = ⌊a/b⌋ and r = a − ⌊a/b⌋b.^[3]

This process of division by means of repeated subtraction is, of course, terribly boring. Even the grade school method of long division uses a significantly more efficient algorithm, in which the digits of the quotient are determined one by one and are in turn used as factors by which the divisor is multiplied. The partial products are subtracted in turn from the dividend. As an example consider the division exercise depicted in Figure 4.4.

Already at the determination of the first digit, 8, of the quotient we are required to make an estimate or else discover it by trial and error. If one makes an error, then one discovers either that the product (quotient digit times divisor) is too large (in the example, larger than 3549), or that the remainder after subtraction of the partial product from the digits of the dividend is larger than the divisor. In the first case the chosen quotient digit is too large, while in the second it is too small, and in either case it must be corrected.

Figure 4.4: Calculational schema for division

This heuristic modus operandi must be replaced in an implementation of a division algorithm by a more precise process. In [Knut], Section 4.3.1, Donald Knuth has described how such rough calculations can be made precise. Let us look more closely at our example.

Let a = (a_{m+n − 1}a_{m+n − 2} … a₀)_B and b = (b_{n − 1}b_{n − 2} … b₀)_B be two natural numbers, represented to the base B, and for b_{n − 1}, the most-significant digit of b, we have b_{n − 1} > 0. We are looking for the quotient q and remainder r such that a = qb + r, 0 ≤ r < b.

Following the long division above, for the calculation of q and r a quotient digit q_j := ⌊R/b⌋ < B is returned in each step, where in the first step R = (a_{m+n − 1}a_{m+n − 2} … a_k)_B is formed from the most-significant digit of the dividend with the largest k for which 1 ≤ ⌊R/b⌋ holds (in the above example at the start we have m + n − 1 = 3 + 3 − 1 = 5, k = 2, and R = 3549). Then we will set R := R − q_jb, where as a control for the correctness of the quotient digit q_j the condition 0 ≤ R < b must be satisfied. Then R is replaced by the value RB + (next digit of the dividend), and the next quotient digit is again ⌊R/b⌋. The division is complete when all digits of the dividend have been processed. The remainder of the division is the last calculated value of R.

A necessity for programming this procedure is to determine, for two large numbers R = (r_nr_{n − 1} … r₀)_B and b = (b_{n − 1}b_{n − 2} … b₀)_B with ⌊R/b⌋ < B, the quotient Q := ⌊R/b⌋ (r_n= 0 is a possibility). Here we take from Knuth the given approximation of Q, which is computed from the leading digits of R and b.

Let

(4.1)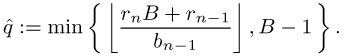 

If b_{n − 1} ≥ ⌊R/b⌋, then for (see [Knut], Section 4.3.1, Theorems A and B),

Under the favorable assumption that the leading digit of the divisor is sufficiently large in comparison to B, then as an approximation to Q, is at most too large by 2 and is never too small.

By scaling the operands a and b this can always be achieved. We choose d > 0 such that db_{n − 1} ≥ ⌊B/2⌋, set â := ad = (â_m+nâ_m+n−1 … â₀)_B, and set := bd = . The choice of d is then made in such a way that the number of digits of never increases in comparison to that of b. In the above notation it is taken into account that â possibly contains one more digit than a (if this is not the case, then we set â_m+n = 0). In any case, it is practical to choose d as a power of 2, since then the scaling of the operands can be carried out with simple shift operations. Since both operands are multiplied by a common factor, the quotient is unchanged; we have ⌊â/⌋ = ⌊a/b⌋.

The choice of in (4.1), which we want to apply to the scaled operators â, respectively , and , can be improved with the following test to the extent that = Q or = Q + 1: If from the choice of we have ≥ () B + , then is reduced by 1 and the test is repeated. In this way we have taken care of all cases in which is too large by 2 at the outset, and only in very rare cases is still too large by 1 (see [Knut], Section 4.3.1, Exercises 19, 20). The latter is determined from the subtraction of the partial product "divisor times quotient digit" from what is left of the dividend. Then for the last time must be reduced by 1 and the remainder updated. The algorithm for division with remainder is now essentially the following procedure.

Algorithm for division with remainder of a = (a_{m+n − 1}a_{m+n − 2} … a₀)_B ≥ 0 by b = (b_{n − 1}b_{n − 2} … b₀)_B > 0

1. Determine the scaling factor d as given above.

2. Set r := (r_m+nr_n+m−1r_m+n−2…r₀)_B ← (0a_m+n−1a_m+n−2 … a₀)_B.

3. Set i ← m + n, j ← m.

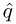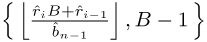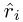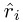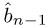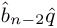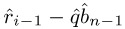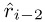4. Set ← min with the digits , − 1, and obtained from scaling by d (see above). If ≥ () B + , set 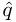← 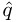− 1 and repeat this test.

5. If r − b 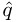< 0, set 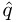← ← 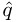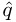− 1.

6. Set r := (r_ir_i−1 …r_i−n)_B ← (r_ir_i−1 … r_i−n)_B − b 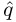and q_j ← .

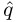7. Set i ← i − 1 and j ← j − 1; if i ≥ n, go to step 4.

8. Output q = (q_mq_m−1 …q₀)_B and r = (r_n−1r_n−2 …r₀)_B.

If the divisor has only a single digit b₀, then the process can be shortened by initializing r with r ← 0 and dividing the two digits (ra_i)_B by b₀ with remainder. Here r is overwritten by the remainder, r ← (ra_i)_B − q_ib₀, and a_i runs through all the digits of the dividend. At the end, r contains the remainder and q = (q_mq_m−1 …q₀)_B forms the quotient.

Now that we have at hand all the requisite processes for implementing division, we present the C function for the above algorithm.

Function:	division with remainder
Syntax:	int div_l (CLINT d1_l, CLINT d2_l, CLINT quot_l, CLINT rem_l);
Input:	d1_l (dividend), d2_l (divisor)
Output:	quot_l (quotient), rem_l (remainder)
Return:	E_CLINT_OK if all is ok E_CLINT_DBZ if division by 0

 int div_l (CLINT d1_l, CLINT d2_l, CLINT quot_l, CLINT rem_l) {   register clint *rptr_l, *bptr_l;   CLINT b_l;   /* Allow double-length remainder plus 1 digit */   clint r_l[2 + (CLINTMAXDIGIT << 1)];   clint *qptr_l, *msdptrb_l, *lsdptrr_l, *msdptrr_l;   USHORT bv, rv, qhat, ri, ri_1, ri_2, bn, bn_1;   ULONG right, left, rhat, borrow, carry, sbitsminusd;   unsigned int d = 0;   int i; 

The dividend a = (a_m+n−1a_m+n−2…a₀)_B and divisor b(b_n−1b_n−2…b₀)_B are copied into the CLINT variables r_l and b_l. Any leading zeros are purged. If the divisor is then equal to zero, the function is terminated with the error code E_CLINT_DBZ.

We allow the dividend to possess up to double the number of digits determined in MAX_B. This makes possible the later use of division in the functions of modular arithmetic. The storage allotment for a doubly long quotient must always be available to the calling function.

    cpy_l (r_l, d1_l);    cpy_l (b_l, d2_l);    if (EQZ_L (b_l))      return E_CLINT_DBZ; 

A test is made as to whether one of the simple cases is at hand: dividend = 0, dividend < divisor, or dividend = divisor. In these cases we are done.

    if (EQZ_L (r_l))      {         SETZERO_L (quot_l);         SETZERO_L (rem_l);         return E_CLINT_OK ;      }    i = cmp_l (r_l, b_l);    if (i == -1)      {         cpy_l (rem_l, r_l);         SETZERO_L (quot_l);         return E_CLINT_OK ;      }    else if (i == 0)      {         SETONE_L (quot_l);         SETZERO_L (rem_l);         return E_CLINT_OK ;      } 

In the next step we check whether the divisor has only one digit. In this case a branch is made to a faster variant of division, which we shall discuss further below.

  if (DIGITS_L (b_l) == 1)    goto shortdiv; 

Now begins the actual division. First the scaling factor d is determined as the exponent of a power of two. As long as b_n−1 ≥ BASEDIV2 := ⌊B/2⌋, the most-significant digit b_n−1 of the divisor is shifted left by one bit, where d, beginning with d = 0, is incremented by 1. Furthermore, the pointer msdptrb_l is set to the most-significant digit of the divisor. The value BITPERDGT − d will be used frequently in the sequel, and therefore it is saved in the variable sbitsminusd.

  msdptrb_l = MSDPTR_L (b_l);  bn = *msdptrb_l;  while (bn < BASEDIV2)    {      d++;      bn <<= 1;    }  sbitsminusd = (int)(BITPERDGT - d); 

If d > 0, then the two most-significant digits of db are computed and stored in bn and bn_1. In this we must distinguish the two cases that the divisor b has exactly two, or more than two, digits. In the first case, binary zeros are inserted into from the right, while in the second case the least-significant digits of come from b_n−3.

  if (d > 0)    {      bn += *(msdptrb_l - 1) >> sbitsminusd;      if (DIGITS_L (b_l) > 2)         {           bn_1 = (USHORT)(*(msdptrb_l - 1) << d) + (*(msdptrb_l - 2) >> sbitsminusd);         }      else         {           bn_1 = (USHORT)(*(msdptrb_l - 1) << d);         }    }  else    {      bn_1 = (USHORT)(*(msdptrb_l - 1));    } 

Now the pointers msdptrr_l and lsdptrr_l are set to the most-significant, respectively least-significant, digit of (a_m+na_m+n−1…a_m+1)_B in the CLINT vector r_l, which will represent the remainder of the division. At the digit a_m+n the variable r_l is initialized to 0. The pointer qptr_l is set to the highest quotient digit.

  msdptrb_l = MSDPTR_L (b_l);  msdptrr_l = MSDPTR_L (r_l) + 1;  lsdptrr_l = MSDPTR_L (r_l) - DIGITS_L (b_l) + 1;  *msdptrr_l = 0;  qptr_l = quot_l + DIGITS_L (r_l) - DIGITS_L (b_l) + 1; 

We now enter the main loop. The pointer lsdptrr_l runs over the digits a_m, a_m−2, …, a₀ of the dividend in r_l, and the (implicit) index i over the values i = m + n, …, n.

  while (lsdptrr_l >= LSDPTR_L (r_l))    { 

As preparation for determining the three most-significant digits of part (a_ia_i−1 … a_i−n)_B of the dividend multiplied by the scaling factor d are calculated and stored in the variables ri, ri_1, and ri_2. The case where the part of the dividend under consideration has only three digits is handled as a special case. In the first pass through the loop there are at least three digits present: On the assumption that the divisor b itself has at least two digits, there exist the most-significant digits a_m+n−1 and a_m+n−2 of the dividend, and the digit a_m+n was set to zero during the initialization of r_l.

      ri = (USHORT)((*msdptrr_l << d) + (*(msdptrr_l - 1) >> sbitsminusd));      ri_1 = (USHORT)((*(msdptrr_l - 1) << d) + (*(msdptrr_l - 2) >> sbitsminusd));      if (msdptrr_l - 3 > r_l)    /* there are four dividend digits */         {           ri_2 = (USHORT)((*(msdptrr_l - 2) << d) +                                           (*(msdptrr_l - 3) >> sbitsminusd));         }      else /* there are only three dividend digits */         {           ri_2 = (USHORT)(*(msdptrr_l - 2) << d);         } 

Now comes the determination of , stored in the variable qhat. Here we distinguish the cases ri ≠ bn (frequent) and ri = b (rare).

      if (ri != bn)    /* almost always */         {           qhat = (USHORT)((rhat = ((ULONG)ri << BITPERDGT) + (ULONG)ri_1) / bn);           right = ((rhat = (rhat - (ULONG)bn * qhat)) << BITPERDGT) + ri_2; 

If bn_1 * qhat > right, then qhat is too large by at least 1 and by at most 2.

          if ((left = (ULONG)bn_1 * qhat) > right)             {               qhat--; 

The test is now repeated only if we have rhat = rhat + bn < BASE due to the decrementing of qhat (otherwise, we already have bn_1 * qhat < BASE² ≤ rhat * BASE).

             if ((rhat + bn) < BASE)               {                 if ((left - bn_1) > (right + ((ULONG)bn << BITPERDGT)))                  {                    qhat--;                  }               }            }         }      else 

In the second, rare, case, ri = bn, first is set to the value BASE − 1 = 2¹⁶ − 1 = BASEMINONE. In this case for rhat we have rhat = ri * BASE + ri_1 − qhat * bn = ri_1 + bn. If rhat < BASE, then a test is made as to whether qhat is too large. Otherwise, we have already bn_1 * qhat < BASE² ≤ rhat * BASE. Under the same condition as above the test of qhat is repeated.

    {       qhat = BASEMINONE;       right = ((ULONG)(rhat = (ULONG)bn + (ULONG)ri_1) << BITPERDGT) + ri_2;       if (rhat < BASE)         {            if ((left = (ULONG)bn_1 * qhat) > right)              {                qhat--;                if ((rhat + bn) < BASE)                  {                     if ((left - bn_1) > (right + ((ULONG)bn << BITPERDGT)))                       {                         qhat--;                       }                   }               }           }     } 

Then comes the subtraction of the product qhat · b from the part u := (a_ia_i−1 … a_i−n)_B of the dividend, which is replaced by the difference thus calculated. Multiplication and subtraction take place at one digit per step. There are two things to note: The products qhat · b_j can have two digits. Both digits of the product are saved for the time being in the ULONG variable carry. The most-significant digit of carry is dealt with as a carry in the subtraction of the next-higher digit.

For the case where the difference u − qhat · b is negative, since here qhat is still too large by 1, as a precaution the value u′ := Bⁿ⁺¹ + u − qhat · b is calculated and the result considered modulo Bⁿ⁺¹ as the B complement Û of u. After the subtraction the highest digit of u′ is located in the most-significant word of the ULONG variable borrow.

That qhat is here too large by 1 is recognized in that ≠ 0. In this case the result is corrected by the addition u ← u′ + b modulo Bⁿ⁺¹. This possibly needed correction is carried out further below.

   borrow = BASE;   carry = 0;   for (bptr_l = LSDPTR_L (b_l), rptr_l = lsdptrr_l;                 bptr_l <= msdptrb_l; bptr_l++, rptr_l++)     {        if (borrow >= BASE)          {             *rptr_l = (USHORT)(borrow = ((ULONG)*rptr_l + BASE -                 (ULONG)(USHORT)(carry = (ULONG)*bptr_l *                    qhat + (ULONG)(USHORT)(carry >> BITPERDGT))));          }        else          {             *rptr_l = (USHORT)(borrow = ((ULONG)*rptr_l + BASEMINONEL -                 (ULONG)(USHORT)(carry = (ULONG)*bptr_l * qhat +                    (ULONG)(USHORT)(carry >> BITPERDGT))));          }     }   if (borrow >= BASE)          {             *rptr_l = (USHORT)(borrow = ((ULONG)*rptr_l + BASE -                              (ULONG)(USHORT)(carry >> BITPERDGT)));          }        else          {             *rptr_l = (USHORT)(borrow = ((ULONG)*rptr_l + BASEMINONEL -                               (ULONG)(USHORT)(carry >> BITPERDGT)));          } 

The quotient digit is stored, subject to a possible necessary correction.

   *qptr_l = qhat; 

As promised, now a test is made as to whether the quotient digit is too large by 1. This is extremely seldom the case (further below, special test data will be presented) and is indicated by the high-valued word of the ULONG variable borrow being equal to zero; that is, that borrow < BASE. If this is the case, then u ← u′ + b modulo Bⁿ⁺¹ is calculated (notation as above).

      if (borrow < BASE)        {           carry = 0;           for (bptr_l = LSDPTR_L (b_l), rptr_l = lsdptrr_l;               bptr_l <= msdptrb_l; bptr_l++, rptr_l++)             {               *rptr_l = (USHORT)(carry = ((ULONG)*rptr_l +                     (ULONG)*bptr_l + (ULONG)*bptr_l +                        (ULONG)(USHORT)(carry >> BITPERDGT)));             }           *rptr_l += (USHORT)(carry >> BITPERDGT);           (*qptr_l)--;        } 

Now the pointers are set to the remainder and the quotient, and we return to the beginning of the main loop.

     msdptrr_l--     lsdptrr_l--;     qptr_l--;   } 

The length of the remainder and that of the quotient are determined. The number of digits is at most 1 more than the number of digits of the dividend minus the number of digits of the divisor. The remainder possesses at most the number of digits of the divisor. In both cases the exact length is set by the removal of leading zeros.

   SETDIGITS_L (quot_l, DIGITS_L (r_l) - DIGITS_L (b_l) + 1);   RMLDZRS_L (quot_l);   SETDIGITS_L (r_l, DIGITS_L (b_l));   cpy_l (rem_l, r_l);   return E_CLINT_OK; 

In the case of "short division" the divisor possesses only the digit b₀, by which the two digits (ra_i)_B are to be divided, where a_i runs through all digits of the dividend; r is initialized with r ← 0 and assumes the difference r ← (ra_i)_B −qb₀. The value r is represented by the USHORT variable rv. The value of (ra_i)_B is stored in the ULONG variable rhat.

 shortdiv:   rv = 0;   bv = *LSDPTR_L (b_l);   for (rptr_l = MSDPTR_L (r_l), qptr_l = quot_l + DIGITS_L (r_l);                   rptr_l >= LSDPTR_L (r_l); rptr_l--, qptr_l--)     {       *qptr_l = (USHORT)((rhat = ((((ULONG)rv) << BITPERDGT) + (ULONG)*rptr_l)) / bv);       rv = (USHORT)(rhat - (ULONG)bv * (ULONG)*qptr_l);     }   SETDIGITS_L (quot_l, DIGITS_L (r_l));   RMLDZRS_L (quot_l);   u2clint_l (rem_l, rv);   return E_CLINT_OK; } 

With t = O(mn), the run time t of the division is analogous to that for multiplication, where m and n are the numbers of digits of the dividend and divisor, respectively, to the base B.

In the sequel we shall describe a number of variants of division with remainder, all of which are based on the general division function. First we have the mixed version of the division of a CLINT type by a USHORT type. For this we return once again to the routine for small divisors of the function div_l(), where it is placed almost without alteration into its own function. We thus present only the interface of the function.

Function:	division of a CLINT type by a USHORT type
Syntax:	int udiv_l (CLINT dv_l, USHORT uds, CLINT q_l, CLINT r_l);
Input:	dv_l (dividend), uds (divisor)
Output:	q_l (quotient), r_l (remainder)
Return:	E_CLINT_OK if all is ok E_CLINT_DBZ if division by 0

We have already indicated that for a given calculation the quotient of a division is not required, and only the remainder is of interest. This will not result in a great savings of time, but in such cases, at least the passing of a pointer to the storage location of the quotient is burdensome. It is therefore worthwhile to create an independent function for computing remainders, or "residues." The mathematical background of the use of this function is discussed more fully in Chapter 5.

Function:	Remainders (reduction modulo n)
Syntax:	int mod_l (CLINT d_l, CLINT n_l, CLINT r_l);
Input:	d_l (dividend), n_l (divisor or modulus)
Output:	r_l (remainder)
Return:	E_CLINT_OK if all is ok E_CLINT_DBZ if division by 0

Simpler than the general case is the construction of the remainder modulo a power of 2, namely 2^k, which is worth implementing in its own function. The remainder of the dividend in a division by 2^k results from truncating its binary digits after the kth bit, where counting begins with 0. This truncation corresponds to a bitwise joining of the dividend to 2^k − 1 = (111111 … 1)₂, the value of k binary ones, by a logical AND (cf. Section 7.2). The operation is concentrated on the digit of the dividend in its representation to base B that contains the kth bit; all higher-valued dividend digits are irrelevant. For specifying the divisor the following function mod_l() is passed only the exponent k.

Function:	remainder modulo a power of 2 (reduction modulo 2k)
Syntax:	int mod2_l (CLINT d_l, ULONG k, CLINT r_l);
Input:	d_l (dividend), k (exponent of the divisor or modulus)
Return:	r_l (remainder)

 int mod2_l (CLINT d_l, ULONG k, CLINT r_l) {   int i; 

Since 2^k > 0, there is no test for division by 0. First d_l is copied to r_l and a test is made as to whether k exceeds the maximal binary length of a CLINT number, in which case the function is terminated.

   cpy_l (r_l, d_l);   if (k > CLINTMAXBIT)     return E_CLINT_OK; 

The digit in r_l in which something changes is determined and is stored as an index in i. If i is greater than the number of digits of r_l, then we are done.

   i = 1 + (k >> LDBITPERDGT);   if (i > DIGITS_L (r_l))     return E_CLINT_OK; 

Now the determined digit of r_l (counting from 1) is joined by a logical AND to the value 2^{kmod BITPERDGT} − 1 (= 2^kmod16 − 1 in this implementation). The new length i of r_l is stored in r_l[0]. After the removal of leading zeros the function is terminated.

   r_l[i] &= (1U << (k & (BITPERDGT - 1))) - 1U;   SETDIGITS_L (r_l, i);   RMLDZRS_L (r_l);   return E_CLINT_OK; } 

The mixed variant of calculating residues employs a USHORT type as divisor and represents the remainder again as a USHORT type, where here again only the interface is given, and we refer the reader to the FLINT/C source code for the short functions.

Function:	remainders, division of a CLINT type by a USHORT type
Syntax:	USHORT umod_l (CLINT dv_l, USHORT uds);
Input:	dv_l (dividend), uds (divisor)
Return:	nonnegative remainder if all is ok 0×FFFF if division by 0

For testing the division there are—as for all other functions as well—some considerations to be taken into account (see Chapter 12). In particular, it is important that step 5 be tested explicitly, though in randomly selected test cases it will appear with a probability of only about 2/B (= 2⁻¹⁵ in our implementation) (see [Knut], Section 4.3.1, Exercise 21).

In the following the given dividend a and divisor b with associated quotient q and remainder r have the effect that the program sequence associated to step 5 of the division algorithm is run through twice, and can therefore be used as test data for this particular case. Additional values with this property are contained in the test program testdiv.c.

The display of test numbers below shows the digits in hexadecimal, running from right to left in ascending order, without specifying the length:

Test values for step 5 of the division
a =	e3 7d 3a bc 90 4b ab a7 a2 ac 4b 6d 8f 78 2b 2b f8 49 19 d2 91 73 47 690d 9e 93 dc dd 2b 91 ce e9 98 3c 56 4c f1 31 22 06 c9 1e 74 d8 0b a4 79 064c 8f 42 bd 70 aa aa 68 9f 80 d4 35 af c9 97 ce 85 3b 46 57 03 c8 ed ca
b =	08 0b 09 87 b7 2c 16 67 c3 0c 91 56 a6 67 4c 2e 73 e6 1a 1f d5 27 d4 e7 8b 3f 15 05 60 3c 56 66 5845 9b 83 cc fd 58 7b a9 b5 fc bd c0 ad 09 15 2e 0a c2 65
q =	1c 48 a1 c7 98 54 1a e0 b9 eb 2c 63 27 b1 ff ff f4 fe 5c 0e 27 23
r =	ca 23 12 fb b3 f4 c2 3a dd 76 55 e9 4c 34 10 b1 5c 60 64 bd 48 a4 e5 fc c3 3d df 55 3e 7c b8 29 bf 66 fb fd 61 b4 66 7f 5e d6 b3 87 ec 47 c5 27 2c f6 fb

^[3]Note that for a < 0 with q = − ⌈|a|/b⌉ and r = b − (|a| + qb) if a ∤ b, respectively r = 0 if a | b, division with remainder is reduced to the case a, b Î .

---

Team-Fly