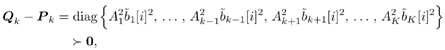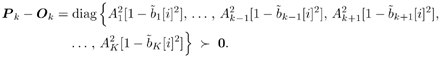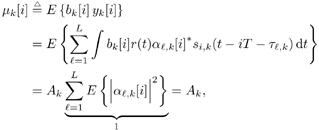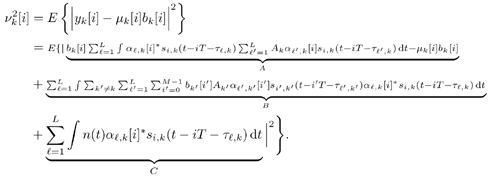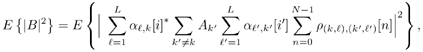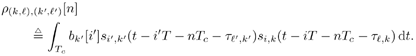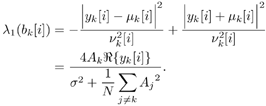6.9 Appendix
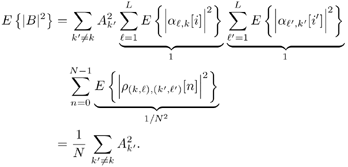
6.9.1 Proofs for Section 6.3.3Proof of Proposition 6.1The proof of this result is based on the following lemma. Lemma 6.1: Let X be a K x K positive-definite matrix. Denote by X k the ( K “ 1) x ( K “ 1) submatrix obtained from X by deleting the k th row and k th column. Also, denote by x k the k th column of X with the k th entry x kk removed. Then we have Equation 6.213 Proof: Since X k is a principal submatrix of X , and X is positive definite, X k is also positive definite. Hence Denote the above-mentioned partitioning of the symmetric matrix X with respect to the k th column and row by In the same way, we partition its inverse: Now from the fact that XY = I K , it follows that Equation 6.214 Equation 6.215 Solving for y kk from (6.214) and (6.215), we obtain (6.213). Proof of (6.60)Using (6.62) and (6.63), by definition we have Equation 6.216 From (6.62) and (6.216) it is immediate that (6.60) is equivalent to Equation 6.217 Equation 6.218 Partition the three matrices above with respect to the k th column and the k th row to get By (6.213), (6.218) is then equivalent to Equation 6.219 Since Equation 6.220 Equation 6.221 we then have Equation 6.222 Therefore, to show (6.219), it suffices to show that Equation 6.223 which is in turn equivalent to [189] Equation 6.224 where X Equation 6.225 Equation 6.226 Hence (6.224) holds and so does (6.60). 6.9.2 Derivation of the LLR for the RAKE Receiver in Section 6.6.2To obtain the code-bit LLR for the RAKE receiver, a Gaussian assumption is made on the distribution of y k [ i ] in (6.182); that is, we assume that Equation 6.227 where m k [ i ] is the equivalent signal amplitude and As in typical RAKE receivers [396], we assume that the signals from different paths are orthogonal for a particular user . Conditioned on b k [ i ], using (6.133) and (6.134), the mean m k [ i ] in (6.227) is given by Equation 6.228 where the expectation is taken with respect to channel noise and all the code bits other than b k [ i ]. The variance Equation 6.229 Using the orthogonality assumption, it is easy to check that A = 0 in (6.229). Since term B and term C in (6.229) are two zero-mean independent random variables , the variance is then given by Equation 6.230 Due to the orthogonality assumption, the second term in (6.230) is given by Equation 6.231 For simplicity, we assume that the time delay t l,k is an integer multiple of the chip duration. Then the first term in (6.230) can be written as Equation 6.232 where Equation 6.233 Assuming that the signature waveforms contain i.i.d. antipodal chips, r ( k,l ),( k',l' )[ n ] is an i.i.d. binary random variable taking values of ±(1/ N ) with equal probability. Since a l,k [ i ], a l',k' [ i' ], and r ( k,l ),( k',l' ) [ n ] are independent, (6.232) can be written as Equation 6.234 Substituting (6.231) and (6.234) into (6.230), we have Equation 6.235 Hence the LLR of b k [ i ] can be written as Equation 6.236 |
EAN: 2147483647
Pages: 91
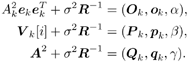
 , we have
, we have