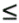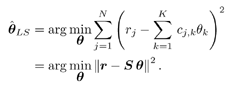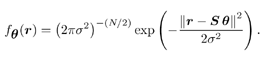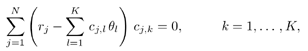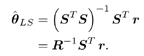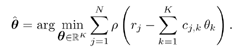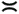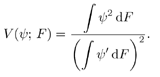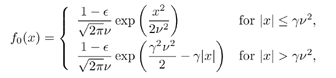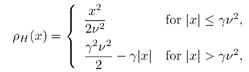4.2 Multiuser Detection via Robust Regression
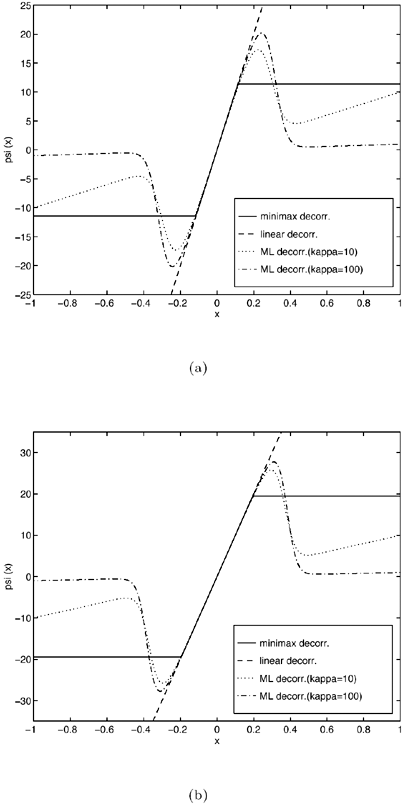
4.2.1 System ModelFor the sake of simplicity, we start the discussion in this chapter by focusing on a real-valued discrete-time synchronous CDMA signal model. At any time instant (until needed in Section 4.5, we will suppress the symbol index i ), the received signal is the superposition of K users' signals, plus the ambient noise, given by (see Section 2.2.1) Equation 4.1 Equation 4.2 where, as before, Equation 4.3 with n > 0, 0 Equation 4.4 This model serves as an approximation to the more fundamental Middleton class A noise model [321, 600] and has been used extensively to model physical noise arising in radar, acoustic, and radio channels. In what follows we discuss some robust techniques for multiuser detection in non-Gaussian ambient noise CDMA channels, which are essentially robustified versions of the linear decorrelating multiuser detector. 4.2.2 Least-Squares Regression and Linear Decorrelator Consider the synchronous signal model (4.2). Denote q K Equation 4.5 or in matrix notation, Equation 4.6 where Equation 4.7 If n j ~ N (0, s 2 ), the pdf of the received signal r under the true parameters q is given by Equation 4.8 It is easily seen from (4.8) that the maximum- likelihood estimate of q under the i.i.d. Gaussian noise assumption is given by the LS solution Equation 4.9 or in matrix form, Equation 4.10 Define the cross-correlation matrix of the signature waveforms of all users as R Equation 4.11 We observe from (4.11) that the LS estimate Equation 4.12 Equation 4.13 4.2.3 Robust Multiuser Detection via M -RegressionIt is well known that the LS estimate is very sensitive to the tail behavior of the noise density [499]. Its performance depends significantly on the Gaussian assumption and even a slight deviation of the noise density from the Gaussian distribution can, in principle, cause a substantial degradation of the LS estimate. Since the linear decorrelating multiuser detector is in the form of the LS solution to a linear regression problem, it can be concluded that its performance is also sensitive to the tail behavior of the noise distribution. As will be demonstrated later, the performance of the linear decorrelating detector degrades substantially if the ambient noise deviates even slightly from a Gaussian distribution. In this section we consider some robust versions of the decorrelating multiuser detector, first developed in [553], which are nonlinear in nature. Robustness of an estimator refers to its performance insensitivity to small deviations in actual statistical behavior from the assumed underlying statistical model. The LS estimate corresponding to (4.7) and (4.9) can be robustified by using the class of M -estimators proposed by Huber [203]. Instead of minimizing a sum of squared residuals as in (4.7), Huber proposed to minimize a sum of a less rapidly increasing function, r , of the residuals: Equation 4.14 Suppose that r has a derivative Equation 4.15 or in vector form, Equation 4.16 where Linear Decorrelating DetectorThe linear decorrelating detector, which is simply the LS estimator, corresponds to choosing the penalty function and its derivative, respectively, as Equation 4.17 Equation 4.18 where a is any positive constant. Notice that the linear decorrelating detector is scale invariant. Maximum-Likelihood Decorrelating DetectorAssume that the i.i.d. noise samples have a pdf f . Then the likelihood function of the received signal r under the true parameters q is given by Equation 4.19 Therefore, the maximum-likelihood decorrelating detector in non-Gaussian noise with pdf f (in the sense that it gives the maximum-likelihood estimate of the product of the amplitude and data bit q K Equation 4.20 Equation 4.21 Minimax Decorrelating Detector We next consider a robust decorrelating detector in a minimax sense based on Huber's minimax M -estimator [203]. Huber considered the robust location estimation problem. Suppose that we have one-dimensional i.i.d. observations X 1 , . . . , X n . The observations belong to some subset c of the real line Equation 4.22 assuming that the noise distribution function belongs to the set of Equation 4.23 where 0 < Equation 4.24 Huber's idea was to minimize the maximal asymptotic variance over P Equation 4.25 This is achieved by finding the least favorable distribution F , that is, the distribution function that minimizes the Fisher information Equation 4.26 over all F Equation 4.27 where k , Equation 4.28 with Equation 4.29 Equation 4.30 The minimax robust decorrelating detector is obtained by substituting r H and y H into (4.14) and (4.15). Assuming that the noise distribution has the Figure 4.1. The y functions for a linear decorrelator, maximum-likelihood decorrelator, and minimax decorrelator under the Gaussian mixture noise model. The variance of the nominal Gaussian distribution is n 2 = 0.01. (a) |
EAN: 2147483647
Pages: 91
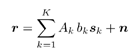
 {+1, “1}, is the normalized signature waveform of the
{+1, “1}, is the normalized signature waveform of the