Multiple Rates of IRR and the MIRR Function

In standard cash flows, there is only one sign change: from negative to positive, or from positive to negative. However, there are cash flows in which the sign can change more than once. In those cases, it is possible that more than one IRR can exist.

Multiple IRRs

Figure 12-15 shows an example that has two IRR calculations, each of which uses a different "seed" value for the guess argument. As you can see, the formula produces different results.

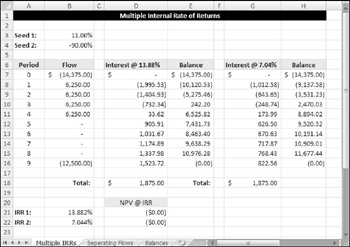
Figure 12-15: The same cash flows can have multiple IRRs.

On the CD 

You can find the workbook with all of the examples in this section,  multiple irr.xlsx, on the companion CD-ROM.

The IRR formula in cell B21 (which returns a result of 13.88%) is

 =IRR(B7:B16,B3) 

The IRR formula in cell B22 (which returns a result of 7.04%) is

 =IRR(B7:B16,B4) 

So which rate is correct? Unfortunately, both are correct. Figure 12-15 shows the interest and running balance calculations for both of these IRR calculations. Both show that the investor can pay and receive either rate of interest, and can secure a (definitional) final balance of $0. Interestingly, the total interest received ($1,875) is also the same.

But there's a flaw. This example illustrates a worst-case scenario of the practical fallacy of many IRR calculations. NPV and IRR analyses make two assumptions:

• You can actually get the assumed (for NPV) or calculated (for IRR) interest on the outstanding balance.

• Interest does not vary according to whether the running balance is positive or negative.

The first assumption may or may not be correct. It's possible that balances could be reinvested. However, in forward-projections in times of changing interest rates, this might not be the case. The real problem is with the second assumption. Banks simply do not charge the same rate for borrowing that they pay for deposits.

Separating Flows

The MIRR function attempts to resolve this multiple rate of return problem. The example in this section demonstrates the use of the MIRR function.

Figure 12-16 shows a worksheet that uses the same data as in the previous example. Rates are provided for borrowing (cell B3) and for deposits (cell B4). These are used as arguments for the MIRR function (cell B19), and the result is 6.1279%:

 =MIRR(B7:B16,B3,B4) 

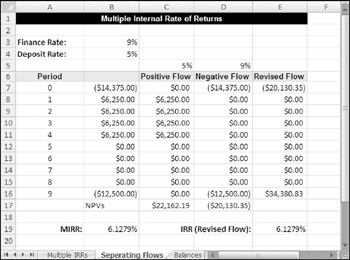
Figure 12-16: Multiple internal rate of return.

The MIRR function works by separating negative and positive flows, and discounting them at the appropriate rate-the finance rate for negative flows and the deposit rate for positive flows.

You can replicate the MIRR algorithm by setting up a revised flow, which compares the two NPVs (refer to Figure 12-16, columns C:E). The negative flow NPV is placed at Period 0, and the positive flow is expressed as its equivalent future value (by accumulating it at the deposit rate) at the end of the investment term. The IRR of the revised flow is the same as the MIRR of the original (source) flow.

This example reveals that the methodology is suspect. In separating negative and positive flows, the MIRR implies that interest is charged on flows. Banks, of course, charge interest on balances. An attempt at resolving the problem is shown in the next example.

Using Balances Instead of Flows

The MIRR function uses two rates: one for negative flows, and one for positive flows. In reality, interest rates are charged on balances and not on flows. The example in this section applies different rates on negative and positive balances. The interest calculation uses an IF function to determine which rate to use.

When analyzing a project in which interest is paid and received, the end balance must be 0 (as shown in Figure 12-17). If it is greater than 0, you have actually received more than the stated deposit rate. If it is less than 0, you still owe money, and the finance rate has been underestimated. This example assumes a fixed finance rate and calculates the deposit rate needed to secure a 0 final balance.

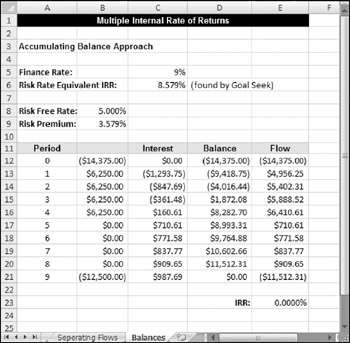
Figure 12-17: Accumulating balance approach for multiple IRRs.

In the Risk Rate Equivalent IRR method, the finance rate is fixed (at 9% in this example). The interest received on positive balances is found by using the Data Data Tools What-If Analysis Goal Seek command. In this example, cell D21 was set to zero by changing cell C6.

The series of flows then becomes the change in the balances, rather than the original given cash flows. The internal rate of return on these balanced-derived flows is zero, or very close to zero. I've already taken into account all the financing and reinvesting necessary for the project, and the resulting interest and return is shown in the flows. The Risk Rate Equivalent IRR may be compared with a different rate such as the Risk Free Rate of Return (traditionally 90-day Treasury bills) to determine the relative risk of the project.

But what does this all mean? If you pay 9% on negative balances, this project returns an 8.579% rate to you on positive balances. The name "Risk Rate Equivalent IRR" refers to the fact that it determines how the project compares with the return on money invested in a bank or 90-day Treasury bills.

There is no requirement that the finance rate be fixed. A bank may do calculations in the same way but fix the deposit rate and allow the Goal Seek feature to calculate the equivalent lending rate.