264.

[Cover] [Contents] [Index]

Page 36

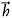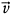imetry, in which horizontally and vertically polarised waves lie in the unit vector and directions, respectively, while unit vector 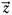denotes the direction of wave propagation. The relationship between unit vectors 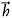, , 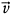and 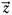can be represented by:

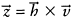(1.26)

The overall electric field can be represented by:

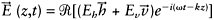(1.27)

where E_h and E_v denote the electric field of vertical and horizontal plane, respectively, which are expressed by:

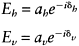(1.28)

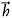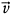The terms a_h and a_v denote the positive amplitudes in the and directions (Figure 1.21), respectively, and the corresponding phases are δ_h and δ_v relative to the phase factor ωt–kz, where ω is frequency, t is time, k is wave number, and z is distance travelled in the 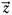direction (i.e. the direction of wave propagation).

In the most general case, the electric field vector of a plane monochromatic wave rotates in a plane perpendicular to the direction of microwave energy propagation and in doing so traces out an ellipse, as shown in Figure 1.21. The wave is said to be elliptically polarised. If one refers to the relative amplitude and phase relationships of the components of a given wave as the elliptic polarisation state, Equation (1.27) can be rewritten as (Zebker et al., 1987):

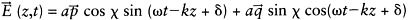(1.29)

where 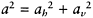is the intensity of the wave, 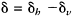is the phase

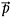angle, both and 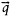are unit vectors in a co-ordinate system rotated by angle Ψ with respect to 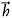, and χ is the ellipticity angle. Note that the width of the ellipse is given by the parameter χ; so that χ=±45° results in left-and right-handed circular polarisations, respectively. The orientation parameter Ψ determines the orientation of the major axis of the ellipse; if χ=0°, then the values Ψ=0° or 180° represent horizontal polarisations, while Ψ=90° represents vertical polarisation.

A polarimetric imaging radar measures the magnitude of the backscatter

[Cover] [Contents] [Index]