Security and Keeping Secrets
| Security is the art of protecting access to information and other computing resources from those whom you do not fully trust. Of course, security is only possible if you are able to keep certain secrets, such as passwords, keys, and so forth. Security is ultimately based on one simple concept: keeping secrets. Indeed, cryptography is the science of keeping secrets. In fact, cryptography is generally nothing more than hiding large secrets (which are themselves awkward to hide) with small secrets (which are more convenient to hide). As we will see in the next section, the large secret is typically referred to as plaintext, and the small secret is referred to as the encryption key. Basic Cryptographic TerminologyA cipher is a system or an algorithm used to transform an arbitrary message into a form that is intended to be unintelligible to anyone other than one or more desired recipients. A cipher represents a transformation that maps each possible input message into a unique encrypted output message, and an inverse transformation must exist that will then reproduce the original message. A key is used by a cipher as an input that controls the encryption in a desirable manner. A general assumption in cryptography work is that the key you choose is the critical secret, whereas the details about the cipher design should not be assumed to be secret. [2] A well-designed encryption algorithm produces an encrypted message that is essentially indistinguishable from a randomly generated byte sequence and provides as little information as possible about the original message to an attacker. A key space is the set of all possible keys that can be used by a cipher to encrypt messages.
The original message is referred to as plaintext . The word plaintext is not meant to imply that the data is necessarily human readable or that it is ASCII text. The plaintext can be any data (text or binary) that is directly meaningful to someone or to some program. The encrypted message is referred to as ciphertext . Ciphertext makes it possible to transmit sensitive information over an insecure channel or to store sensitive information on an insecure storage medium. Examples of such applications are Secure Sockets Layer (SSL) and the NTFS Encrypted File System (EFS), respectively. The term encryption refers to the process of transforming plaintext into ciphertext. Decryption is the inverse process of encryption, transforming ciphertext back into the original plaintext. Figure 2-1 shows how a symmetric [3] cipher is used to encrypt a confidential message.
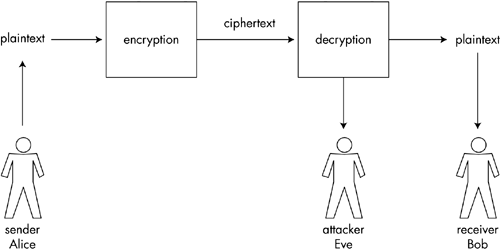
Figure 2-1. Symmetric encryption. A sender refers to someone who encrypts a plaintext message and sends the resulting ciphertext to an intended recipient. The intended recipient is referred to as the receiver . Anyone who tries to get between the sender and receiver with the intention of obtaining the key and/or the plaintext message is referred to as an attacker . An attacker is also known by other names , including interloper, villain, and eavesdropper . Figure 2-2 shows the relationship between sender, receiver, and attacker. To make a cryptographic scenario more vivid , these characters are often portrayed in cryptographic literature as protagonists named Alice and Bob, and a villain named Eve. In more complex scenarios, additional characters are often brought into the story. These characters can be very useful for clearly describing complex cryptographic protocols in a familiar manner. Figure 2-2. Sender, receiver, and attacker, a.k.a. Alice, Bob, and Eve. The design and application of ciphers is known as cryptography, which is practiced by cryptographers . The breaking of ciphers is known as cryptanalysis . Because cipher designs must be thoroughly tested , cryptanalysis is also an integral part of designing ciphers. Cryptology refers to the combined mathematical foundation of cryptography and cryptanalysis. A cryptanalytic attack is the application of specialized techniques that are used to discover the key and/or plaintext originally used to produce a given ciphertext. As was previously mentioned, it is generally assumed that the attacker knows the details of the cipher and only needs to determine the particular key that was employed. Another important concept that you should be aware of is represented by the word break . When a break has been discovered for a particular algorithm (i.e., the algorithm is said to have been broken), it does not necessarily mean that an effective means has been found to attack the algorithm in practice. A break is a more theoretical concept, which simply means that a technique has been found that reduces the work required for an attack to fall below that of a brute-force approach in which all possible keys are tested. The breaking attack may well still be out of reach given existing computational power in the real world. Although the discovery of such a break does not necessarily imply that the algorithm is vulnerable in the real world, it is generally no longer considered suitable for future usage. After all, why not play it safe? Secret Keys Versus Secret AlgorithmsAn important aspect of any effective cipher is the fact that the efficacy of the cipher is entirely based on the secrecy of the key, not on the secrecy of the cipher algorithm. [4] This may seem counterintuitive at first, since it would appear that a secret algorithm would be a great idea. However, it is very hard to keep an algorithm secret and much easier to keep a simple key secret. You could imagine many problems with the secret algorithm approach: What do you do when one person in your trusted group becomes untrusted? It would be easier to change keys than to change algorithms. What if you suspect that your cipher algorithm has been compromised? If your key becomes compromised, you would naturally change to a new key. Changing algorithms would be much more difficult. If you rely on the secrecy of the cipher algorithm, then these scenarios require you to replace your entire cryptographic infrastructure, forcing you to select an entirely new secret algorithm. On the other hand, if only a secret key is compromised, then you simply need to randomly select a new secret key and continue using your existing cryptographic infrastructure.
The idea of depending on the secrecy of an algorithm is often referred to as secrecy through obscurity, which is analogous to hiding your valuables in an obscure but insecure location, such as under your mattress. Relying on a well-known but powerful algorithm is a much more secure approach, which is analogous to storing your valuables in a hardened bank vault. Several strong standard algorithms exist, which have been heavily studied and tested. Never use an algorithm that you design yourself (unless you happen to be a world-class cryptographer), and never use a proprietary algorithm offered by the many snake oil vendors out there. If you see any proprietary algorithm advertisement that makes claims such as "perfect security" and " unbreakable ," you know that the algorithm is almost certainly weak. Real cryptographers never use such phrases. By using a respected, well-known, published cipher algorithm, you benefit from the analysis and attacks carried out by the many researchers in the cryptographic community. This goes a long way in helping you gain trust in the cryptographic strength of the cipher you choose to use. Also, there is always a tremendous advantage in adopting standards. This generally reduces costs, increases implementation choices, and improves interoperability. Obviously, if you use a standard cipher algorithm, then the algorithm itself cannot be much of a secret! Examples of established cryptographic standards that we discuss in later chapters include
Note that DES has technically been broken, but it is still considered to be quite strong. We shall see that DES, Triple DES, and AES are symmetric algorithms used for bulk data encryption. RSA and DSA are asymmetric algorithms used for key exchange and digital signature authentication, respectively. SHA is a hashing algorithm used for several cryptographic purposes. Classical Techniques for Keeping SecretsOver the course of human history, secret-keeping and secret-breaking technologies have developed in a continuous struggle resembling the game of leapfrog . We now look at a few simple, classical ciphers. Although you would never actually use these techniques today, they are helpful in clearly seeing the big conceptual picture and introducing some of the mathematical concepts. THE CAESAR CIPHERTo see how some of the terminology is applied to a concrete scenario, we now consider a very simple cipher that is attributed to Julius Caesar. You could imagine that if anyone ever needed cryptography, Caesar most certainly did! [5] By modern standards, this cipher is trivial to break, and so it has little real-world application today, but it has the virtue of simplicity, and it will therefore serve us well as a gentle introduction to the topic of ciphers. Starting in the next chapter, we look at much more effective modern ciphers.
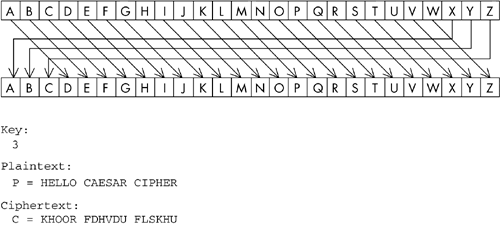
In the Caesar cipher, each plaintext letter is shifted by three so that A is replaced with D, B is replaced with E, and so on. This wraps around so that X is replaced with A, Y is replaced with B, and Z is replaced with C. The Caesar cipher shifts each letter by three, but in a generalized sense this cipher can be thought of as a shift by k, where k is an integer that can be considered the cipher's key. In this chapter we refer to this generalized shift cipher as the Caesar cipher without being too concerned with historical accuracy. Because each individual character is replaced by a specific corresponding character, this cipher is a monoalphabetic cipher. Figure 2-3 shows the simple mapping that takes place in the Caesar cipher. Figure 2-3. The Caesar cipher. To cut our technical teeth, let's look at the definition of the Caesar cipher expressed in mathematical notation. The nice thing about mathematical notation is that it is exceedingly precise and concise . Another good thing about using formal mathematics is that when you have proven a theorem, you know exactly what you have proved, and the result may then be used in proving other theorems. The unpleasant thing about it is that it can give some folks a headache . Although this is such a simple cipher that a mathematical treatment is probably not necessary, more complex ciphers can be understood in their entirety only by devising a rigorous mathematical representation. Therefore, if you want to seriously pursue cryptography, it is recommended that you learn a modicum of several branches of mathematics, including number theory and abstract algebra. In any case, the next page shows the Caesar cipher in mathematical terms. [6]
You can see that this mathematical definition does not concern itself with real-world details, such as the letters from A to Z that are to be used in the message. Instead, the characters in the plaintext and ciphertext are symbolized by the integers from 0 to 25 rather than a by more realistic choice, such as ASCII or Unicode values. Other details, such as dealing with punctuation and spaces, are also ignored. In this definition E k is the encryption function, D k is the decryption function, and k is the encryption key. The standard notation Z 26 represents the set of integers {0,1,2,3, 25}. The term (mod 26) indicates that we are using modular arithmetic, with a modulus of 26, rather than regular grade-school arithmetic. For a description of modular arithmetic, please see Appendix B on cryptographic mathematics. If you would like to see a C# implementation of this cipher, look at the CaesarCipher code example provided. The implementation is straightforward, so we omit the code listing here; however, you may want to look at the source code provided. If you run this program, you will notice that it can deal with characters in the ranges A to Z plus the space character. It does not accept any lowercase characters or nonalphabetic characters. It prompts you for a key from 0 to 25, and it rejects any value outside of this range. A typical run of the CaesarCipher example produces the following output. [View full width]
If you are a frequent user of Usenet, you may be familiar with an encoding known as ROT13. This is actually the Caesar cipher, but with a key k = 13. Because ROT13 is extremely easy to break, it is never used for true encryption. However, Usenet [9] client programs typically provide a ROT13 capability for posting messages that might offend some people or to obscure the answers to riddles, and so on. Anyone can easily decipher it, but it involves an intentional act by the reader to do so. The nice thing about ROT13's key value of 13 is that the same key can be used for encoding and decoding.
BRUTE-FORCE ATTACK: CRACKING THE CAESAR CIPHERThe term brute-force search refers to the technique of exhaustively searching through the key space for an intelligible result. To do this on the Caesar cipher, you would start with k = 1 and continue toward k = 25 until a key is found that successfully decrypts the ciphertext to a meaningful message. Of course, k = 0 or k = 26 would be trivial, since the plaintext and ciphertext would be identical in those cases. The CaesarCipherBruteForceAttack code example shows an implementation of this attack. class CaesarCipherBruteForceAttack { static void Main(string[] args) { ... //exhaustively test through key space for (int testkey=1; testkey<=25; testkey++) { Console.Write("testkey: {0,2} produced plaintext: ", testkey); StringBuilder plaintext = Decrypt (ciphertext, testkey); Console.WriteLine(plaintext); } } ... static StringBuilder Decrypt (StringBuilder ciphertext, int key) { StringBuilder plaintext = new StringBuilder(ciphertext.ToString()); for (int index=0; index<plaintext.Length; index++) { if (ciphertext[index] != ' ') { int character = (((ciphertext[index]+26-'A')-key)%26)+'A'; plaintext[index] = (char)character; } } return plaintext; } } For example, assume that you have the ciphertext KHOOR , and you know that it was encrypted using a Caesar-style shift cipher. The following output from the CaesarCipherBruteForce example program shows all possible decryptions for this ciphertext, using each of the 25 possible keys. Note that only the result HELLO appears to be meaningful, so the key value k = 3 appears to be the correct key. Of course, in an actual brute-force search attack, you would quit as soon as you found the correct key, but we show them all in the following program output listing. Enter uppercase ciphertext: KHOOR testkey: 1 produced plaintext: JGNNQ testkey: 2 produced plaintext: IFMMP testkey: 3 produced plaintext: HELLO testkey: 4 produced plaintext: GDKKN testkey: 5 produced plaintext: FCJJM testkey: 6 produced plaintext: EBIIL testkey: 7 produced plaintext: DAHHK testkey: 8 produced plaintext: CZGGJ testkey: 9 produced plaintext: BYFFI testkey: 10 produced plaintext: AXEEH testkey: 11 produced plaintext: ZWDDG testkey: 12 produced plaintext: YVCCF testkey: 13 produced plaintext: XUBBE testkey: 14 produced plaintext: WTAAD testkey: 15 produced plaintext: VSZZC testkey: 16 produced plaintext: URYYB testkey: 17 produced plaintext: TQXXA testkey: 18 produced plaintext: SPWWZ testkey: 19 produced plaintext: ROVVY testkey: 20 produced plaintext: QNUUX testkey: 21 produced plaintext: PMTTW testkey: 22 produced plaintext: OLSSV testkey: 23 produced plaintext: NKRRU testkey: 24 produced plaintext: MJQQT testkey: 25 produced plaintext: LIPPS It may have occurred to you that for some ciphertexts, it is possible that more than one key might result in intelligible plaintext, causing uncertainty about whether or not you have discovered the true key. For example, assume that you have the very short cipher text WZR, and you know that it was produced using the Caesar cipher. If you perform a brute-force key search using the CaesarCipherBruteForce program, you will see three plausible plaintext results: TWO (key k = 3), RUM (key k = 5), and LOG (key k = 11). However, keep in mind that as the number of characters in the known ciphertext increases, the probability of finding more than one meaningful plaintext result diminishes quickly. This concept has been mathematically formalized , and it is referred to as the unicity distance of the cipher. The unicity distance is a measure of how much ciphertext is needed to reduce the probability of finding spurious keys in a brute-force search, close to zero. It is therefore also an indication of how much ciphertext is required (at least with a hypothetical computer of arbitrary power) to obtain the key from the ciphertext. Unicity distance depends on the statistical characteristics of both the possible plaintext messages and the mechanics of the cipher. You may be wondering what "meaningful" means in the context of meaningful results. What if the plaintext could be written in any spoken language? Then, all sorts of results could be considered meaningful, making the attack on the cipher more problematic . [10]
What if the plaintext was compressed before it was enciphered ? Then, just about nothing would be human readable, and nothing would appear to be meaningful. However, in modern cryptography, we generally assume that the attacker knows all of these details. In real life, this may not always be the case, but for the purposes of analyzing a cipher design, it should be assumed that the attacker knows what plaintext would be meaningful. It is also assumed that the attacker knows all the details of the cipher implementation. For example, if the plaintext is compressed before being encrypted, then we should assume that the attacker knows the entire cipher operation, including the compression step. If an obscure language is used, it is assumed that the attacker understands that language as well. In general, we assume that the attacker knows everything except for the secret key and the plaintext he or she is seeking. You may notice that if you apply the Caesar cipher multiple times, you do not actually increase the strength of the cipher one iota. For example, if you encrypt the text CAT with k = 6 to get IGZ, and then encrypt that result with k = 4 to get MKD, you have effectively done nothing more than simply encrypt once with k = 10, since 4 + 6 = 10. This is analogous to the fact that if you apply a compression algorithm to a file that has already been compressed, you will typically find that you have not achieved much if any additional compression. Many ciphers experience diminished gains when applied repeatedly in this way; however, Triple DES, [11] described in Chapter 3, is an effective cipher that employs repeated application of the same algorithm (but with different keys) as part of its implementation.
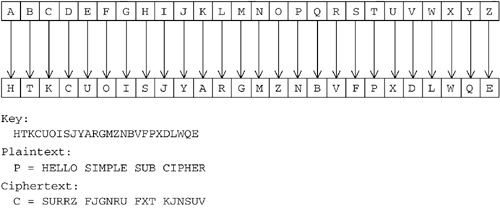
Needless to say, the Caesar cipher is not a very strong cipher by modern standards, but perhaps we should not be asking too much of a 2,000-year-old cipher. A ciphertext-only attack requires just a simple program to exhaustively test the very small key space of 25 keys. In the case of a known plaintext attack, the work is trivial, since the plaintext and its corresponding ciphertext can be compared, and the key that was used becomes visually obvious. We will look at an improved classical cipher named the Vigen re cipher, as well as at some more powerful modern ciphers, later in this chapter. But first, let's look at another simple classical cipher with a much larger key space. THE SIMPLE SUBSTITUTION CIPHERThe simple substitution cipher was used quite unsuccessfully by Queen Mary [12] of Scotland. In this substitution cipher, each character of the plaintext is replaced by a particular corresponding character in a permuted alphabet, making it (like the Caesar cipher) another type of monoalphabetic substitution cipher. This means that there is a one-to-one mapping between the characters of the plaintext and the ciphertext alphabets. This is not a good thing, because this makes the cipher vulnerable to frequency-analysis attacks. This attack can be understood if you consider that the relative frequencies of individual characters remain unchanged. Also, common character combinations such as qu and the (in English) end up as statistically detectable character sequences in the resulting ciphertext. Figure 2-4 shows how a simple substitution cipher works. The key used in this example is one of a large number of possible values.
Figure 2-4. Simple substitution cipher. How many possible values are there for the key k ? There are 26 factorial [13] permutations on a 26-letter alphabet. That means that this cipher has a key space approximately equivalent to an 88-bit key, since 26! = 403,291,461,126,605,635,584,000,000, which falls between 2 88 and 2 89 . This is much larger than the key space of the Caesar cipher (with only 25 keys), but, as we shall see, this cipher is surprisingly only a very small improvement over the Caesar cipher. The main reason for this is that it is still very easy to attack using the frequency-analysis attack technique. This proves the very important lesson that a large key size is necessary but not sufficient to guarantee security.
To understand how we calculated this large number, imagine that you are given the task of making an arbitrary permutation of the English alphabet. You have to make a sequence of choices. On the first choice you can choose any one of the 26 letters in the alphabet for the first letter of the permutation. On the second choice you can choose any one of the remaining 25 letters for the second letter of the permutation. On the third choice you can choose any one of the remaining 24 letters, and so on. On the last choice, there is just one letter remaining. So, in all there are 26 · 25 · 24 · · 2 · 1 different ways to make these choices, which is defined as 26! in mathematical notation. Here is the definition of the simple substitution cipher expressed in mathematical notation.
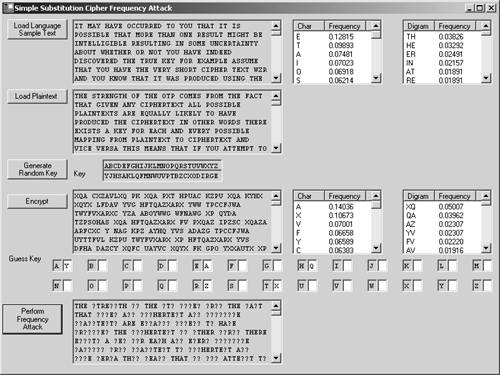
The code example SimpleSubCipher demonstrates this cipher. Again, the code is fairly simple, so we shall not list it here, but if you are interested, you can look at the C# source code in the provided project. The output of this program is shown as follows. Enter uppercase plaintext: HELLO SIMPLE SUB CIPHER Enter 26 char key permutation: HTKCUOISJYARGMZNBVFPXDLWQE Resulting ciphertext: SURRZ FJGNRU FXT KJNSUV Recovered plaintext: HELLO SIMPLE SUB CIPHER Notice how the double letters LL in HELLO are replaced with the double letters RR in the ciphertext. This is a telltale sign that leads into the next section, describing the statistical type of attack on this cipher, which was used against poor Mary Stuart, Queen of Scots. FREQUENCY ANALYSIS: CRACKING THE SUBSTITUTION CIPHERWith the simple substitution cipher, you can generally use a frequency-analysis attack that employs statistical methods . This takes advantage of the varying probability distribution of letters and letter sequences in typical plaintext. The idea is based on the fact that, for example, in English, the letters E, T, and A are more frequent than other letters. Letter pairs such as TH, HE, SH, and CH are much more common than other pairs, such as TB or WX. Of course, a Q is virtually always followed by a U. This uneven probability distribution indicates that English (or any other natural language) is full of redundancy. Redundancy serves an important purpose: It reduces the probability of transmission errors. Unfortunately , redundancy is also a friend of the attacker. The code example SimpleSubCipherFrequencyAttack demonstrates this attack. The example program is a bit complicated, but the basic idea behind how it works is quite simple. If you try running this program, you will see that it loads a sample file containing English text. Then it loads a plaintext file, generates a random key (i.e., a random permutation of the alphabet), and encrypts the plaintext. The resulting ciphertext is then displayed, and some statistical data for both the sample text and the ciphertext can be used to help you guess at the various letter substitutions in the key. The actual key and plaintext is displayed, but try to use the program to decipher it without looking at the key or plaintext. As you try solving this puzzle, you will find that it is slightly similar to the thought process used for a crossword puzzle or the television game show Wheel of Fortune . This program is interactive, it relies on your own intuition, and it is based on displaying a few simple statistics. This program could be enhanced by incorporating more statistical analysis and heuristic decision making to completely automate the attack. This will not be done here, since this cipher is not typically used in modern times. However, the basic concept of frequency analysis that we see being used here is also used in cracking much more powerful ciphers as well. Figure 2-5 shows the frequency attack on the simple substitution cipher in progress. Figure 2-5. Cracking the simple substitution cipher using frequency analysis. THE VIGEN ˆRE CIPHERWith the advent of the telegraph [14] in the mid 1800s, there was an increased interest in cryptography, and it was well known that any monoalphabetic substitution cipher was too vulnerable to frequency analysis. The Victorian solution to this problem was to adopt the Vigen re cipher, which oddly enough had already existed for almost 300 years . [15] This cipher was known in French as le chiffre ind chiffrable, which in English means the "undecipherable cipher." This was indeed a formidable cipher for its time. In fact, the Vigen re cipher remained unbroken for almost three centuries, from its invention in 1586 [16] until long after its defeat in 1854, when Charles Babbage [17] was finally able to break it. [18] It is interesting to note that this cipher had a very short shelf life once it was applied on a large scale to telegraphy. This seems to show how quickly cryptographic technology can become obsolete once there is a compelling interest in breaking it. This can make one nervous about the security of today's encrypted data. What modern-day Babbage might be lurking out there now?
The Vigen re cipher is a polyalphabetic substitution cipher. That means that multiple alphabet mappings are used, thereby obscuring the relative frequencies of characters in the original plaintext. Therefore, unlike the monoalphabetic ciphers (such as Caesar and simple substitution) the Vigen re cipher is immune to simple frequency analysis. Effectively, the Vigen re cipher changes the mapping of plaintext characters to ciphertext characters on a per-character basis. It is based on the table shown in Figure 2-6. Each row of the table is actually a Caesar cipher shifted by a number according to its row position. Row A is shifted by 0, row B is shifted by 1, and so on. Figure 2-6. The Vigen re cipher. The Vigen re cipher combines this table with a keyword to encrypt plaintext. For example, assume that you want to encrypt the plaintext GOD IS ON OUR SIDE LONG LIVE THE KING with the key PROPAGANDA. To encrypt this plaintext, you repeat the key as many times as is required to span the length of the plaintext, writing it below the plaintext. Then, each ciphertext character is produced by taking the column determined by the corresponding plaintext character and intersecting it in the table with the row determined by the corresponding keyword character. For example, the first plaintext character G is combined with the first keyword character P, and as you can see in Figure 2-6, the column and row intersect on the resulting first ciphertext character V. Each subsequent ciphertext character is determined in the same way. Plaintext: GOD IS ON OUR SIDE LONG LIVE THE KING Keyword PRO PA GA NDA PROP AGAN DAPR OPA GAND Ciphertext: VFR XS UN BXR HZRT LUNT OIKV HWE QIAJ To decrypt the ciphertext, write the repeated key below the ciphertext. Each character of plaintext is recovered by taking the row corresponding to the key and finding the column that contains the ciphertext character in that row. Then, take the character at the top of that column, and you have the original plaintext character. Ciphertext: VFR XS UN BXR HZRT LUNT OIKV HWE QIAJ Keyword: PRO PA GA NDA PROP AGAN DAPR OPA GAND Plaintext: GOD IS ON OUR SIDE LONG LIVE THE KING This procedure is a bit tedious , but it can be accomplished using pencil and paper. You might prefer to run the VigenereCipher program example and inspect its code. You will see that it produces the same results as the pencil-and-paper approach described above. Here is the definition of the Vigen re cipher expressed in mathematical notation.
If you run the VigenereCipher program example, you will see that it produces output similar to the following. Enter plaintext: GOD IS ON OUR SIDE LONG LIVE THE KING Enter keyword: PROPAGANDA Resulting ciphertext: VFR XS UN BXR HZRT LUNT OIKV HWE QIAJ Recovered plaintext: GOD IS ON OUR SIDE LONG LIVE THE KING BABBAGE'S ATTACK: CRACKING THE VIGEN ˆRE CIPHERSince a polyalphabetic substitution cipher involves the use of multiple alphabet mappings, this eliminates the one-to-one relationship between each plaintext character and ciphertext character. The result is that there is now a one-to-many relationship between each character and its corresponding character in the ciphertext. Although frequency analysis alone is unable to break this cipher, Babbage found that using a combination of key analysis and frequency analysis did the trick. How do you proceed with Babbage's attack? First, you perform key analysis to try to determine the length of the key. Basically, you look for periodic patterns of coincidence in the ciphertext. To do this, you shift the ciphertext by one character against itself, and the number of matching characters is counted. It is then shifted again, and matching characters are counted again. This is repeated many times, and the shifts with the largest matching counts are noted. A random shift will give a low number of matching characters, but a shift that is a multiple of the key length will statistically give a higher matching count. This results naturally from the fact that some characters are more frequent than others together with the fact that the key is used many times over in a repeating pattern. Since a character will match a copy of itself that has been encrypted with the same key letter, the match count goes up slightly for shifts that are equal to multiples of the key length. Obviously, this requires a large enough ciphertext to work well, since the unicity distance for this cipher is much larger than that of a monoalphabetic substitution cipher. Once the key length has been estimated, the next step is to perform frequency analysis. To do this, you segregate the characters of the ciphertext that have been encrypted with the same key letter into their own groups, based on the assumed key length. Each grouping of characters is then treated as a simple Caesar-style shift using either brute-force or frequency analysis techniques. Once these individual groups have been deciphered, they are reassembled into the final recovered plaintext result. When you see how this works, you will realize that it is not all that difficult a concept, and you may be surprised that this cipher was able to stand up against 300 years of cryptanalysis. Other, more sophisticated polyalphabetic ciphers may also be attacked using similar techniques if the key period is not too long. THE ONLY PROVABLY UNBREAKABLE CIPHER: ONE-TIME PADThere is only one cipher that is theoretically 100 percent secure, known as the One-Time Pad [19] (OTP). To achieve this perfect security, the OTP has certain stringent requirements: the keys must be truly randomly generated, the keys must be kept strictly secret, and the keys must never be reused. Unlike other types of ciphers, the OTP (or any of its mathematical equivalents) is the only cipher that has been mathematically proven to be unbreakable. The OTP boasts perfect security, but the downside is that key management is very problematic. For this reason, the OTP is typically used only in situations where secrecy is of the utmost importance and the bandwidth requirements are low. Examples of this are probably rare, but it has been used in many military, diplomatic, and espionage scenarios.
Let's look at how it works. To use the OTP cipher, you randomly generate a new one-time key that contains the same number of bytes as the plaintext. Then, the plaintext is combined with the key on a bit-by-bit basis, using an invertible operator, such as the exclusive-or operator, to produce the ciphertext. The exclusive-or operator is often abbreviated as XOR and mathematically represented with the Table 2-1. The XOR Operator
The XOR operator is not the only choice for the OTP. Actually, any invertible operator could be used. For example, consider the operator used in the Caesar cipher, [20] adding the corresponding key byte to the plaintext byte, modulo 256. This is basically the same as the Caesar cipher except that instead of using the same key value on every byte in the plaintext, a new, randomly chosen key byte is applied to each individual byte in the plaintext. The slight advantage of using the XOR operator is that it is its own inverse, but mathematically, it can be shown that there is really no significant difference between these two choices.
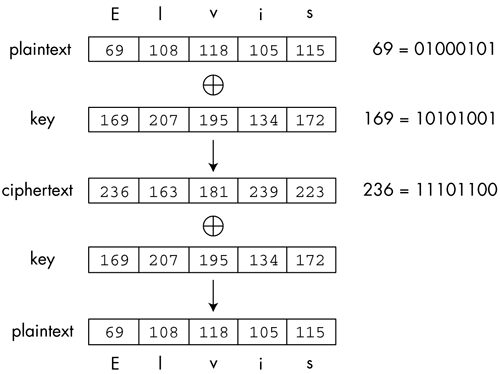
Figure 2-7 shows how the OTP cipher works. The word Elvis is encoded in ASCII as 69, 108, 118, 105, 115 (in base 10). The random key is 169, 207, 195, 134, 172. The result of the XOR operation produces 236, 163, 181, 239, 223. On the right side of the figure, you can see the binary representation of the first bytes of the plaintext, key, and ciphertext. Figure 2-7. The One-Time Pad cipher. Mathematically, the OTP cipher is described as follows.
The OTP_XOR code example shows an implementation of this. The method EncryptDecrypt performs both encryption and decryption because XOR is its own inverse. static void Main(string[] args) { Console.Write("Enter plaintext: "); StringBuilder plaintext = new StringBuilder(Console.ReadLine()); RandomNumberGenerator rng = new RNGCryptoServiceProvider (); byte[] key = new Byte[100]; rng.GetBytes(key); StringBuilder ciphertext = EncryptDecrypt (plaintext, key); Console.WriteLine("ciphertext: {0}", ciphertext); StringBuilder recoveredplaintext = EncryptDecrypt (ciphertext, key); Console.WriteLine("recovered plaintext: {0}", recoveredplaintext); } static StringBuilder EncryptDecrypt (StringBuilder data_in, byte [] key) { StringBuilder data_oput = new StringBuilder(data_in.ToString()); for (int index=0; index<data_in.Length; index++) { int character = ((int)data_in[index] ^ key[index]); data_oput[index] = (char)character; } return data_oput; } A typical run of the OTP_XOR code example produces the following. Each time you run it, you will see a different ciphertext, because the OTP key is randomly generated each time. Enter plaintext: hello ciphertext: IE3c recovered plaintext: hello The strength of the OTP comes from the fact that given any ciphertext, all possible plaintexts are equally likely to have produced the ciphertext. In other words, there exists a key for each and every possible mapping from plaintext to ciphertext, and vice versa. This means that if you attempt to perform a brute-force key-search attack on an OTP ciphertext, you will find that every possible plaintext result will occur in your results. This will include every single possible result, including all those that may appear meaningful. This clearly gets you nowhere. The thing to remember about the OTP is that brute force is futile and irrelevant! The only hope in cracking an OTP encrypted message is if the key is used multiple times on different messages, or the algorithm used to produce the pseudorandom key has predictabilities that you can capitalize on, or you somehow manage to obtain the key through noncryptographic means. You can convince yourself of this fact by considering the following argument. Assume that your plaintext is just one byte long. Then, according to the definition of the OTP cipher, the key must also be one byte long. Choose any given plaintext from the set of 256 possible 8-bit plaintext messages. If you then XOR each of the 256 possible keys with the chosen 8-bit plaintext, you will produce 256 distinct 8-bit ciphertext messages. The fact that the ciphertext messages are all distinct is because the XOR operator is lossless in an information theoretic sense. This means that by choosing the appropriate key, you can encrypt any 8-bit plaintext into any 8-bit ciphertext. The argument works equally well in the reverse direction, so that by choosing the appropriate key, you can decrypt any 8-bit ciphertext into any 8-bit plaintext. There is simply no way to know which is the correct key. The OTP does have its problems, however, and if it is not implemented perfectly, it is not completely secure. First, if the same OTP key is ever used more than once, it is no longer 100 percent secure. Second, the security of the OTP is also dependent on the randomness of the key selection. A deterministic algorithm simply cannot generate a truly random sequence of bytes. Even the best deterministic random number generator design cannot produce anything better than pseudorandom numbers . Third, the key length is typically much larger than we would like it to be and must be generated anew for every single message. Since the key is the same length as the message, and the message is of arbitrary length, then the problem of key distribution becomes a significant issue. Key distribution refers to the fact that both the sender and receiver need a copy of the key to effectively communicate with one another. The catch-22 question then arises: If you have a secure enough channel to transmit the new key each time, why can't you just send the actual message via that secure channel? Alternatively, you could ask, If the channel is insecure enough to require encryption in the first place, how can you justify transmitting the OTP keys via that channel? Well, the answer is that the OTP is occasionally useful in situations where you temporarily have a very secure channel, during which time you quickly exchange as many keys as you expect are needed, and then store them locally in a secure manner. [21] Then, at other times, when you do not have the luxury of a secure channel, you encrypt your messages with your stockpile of OTP keys. The only thing that must be carefully managed is that the sender and receiver must use the keys in the proper order to ensure that they will use the same key for encryption and decryption on each individual message. Historically, the Nazis used the OTP cipher during World War II in diplomatic correspondence. [22] When the Nazi diplomats were back in Berlin, they would have a very secure environment to exchange a large set of new OTP keys. Then, when they were back out in the field, the insecure telegraph, telephone, and radio channels could be used for confidential messages that were encrypted using those keys. The British also made good use of the OTP cipher. [23]
Brute-Force Attack Work FactorThe amount of work it takes to accomplish a computational goal is referred to as its work factor . Calculating the work factor for breaking a cipher is an important aspect of analyzing cipher effectiveness. We now briefly look at calculating brute-force attack work factors. As we have seen, the Caesar cipher is pretty pathetic, since its key space is so tiny ”not to mention its other serious weaknesses. With only 25 keys, the key space is equivalent in an information theoretic sense to a tiny, 6-bit key, since 2 to the power of 6 equals 32, which is large enough to represent all 25 key values. Fortunately, there are ciphers with much larger key spaces. The good news for Alice and Bob, and bad news for Eve, is that the brute-force attack work factor grows exponentially as a function of the key size. Mathematically, for an n -bit key, the work factor is W a 2 n . Of course, if Eve can find an attack that is significantly more efficient than brute force, things could get a bit iffier. Thus, more powerful ciphers require more sophisticated attacks than the brute-force key search just described. This is because, for very large key spaces, an exhaustive test on each possible key would simply take too long. For example, if a given cipher employs a key that is 128 bits long, then there are 2 to the power of 128 possible keys. This is a horrendously large number of keys! In base 10, this number is represented using 39 digits! Keep in mind that a large enough key is necessary, but not sufficient, to guarantee cipher security. 2^128 = 340,282,366,920,938,463,463,374,607,431,768,211,456 Ignoring insignificant details, such as leap years, the number of seconds per year is 60 sec/min * 60 min/hr * 24 hr/day * 365 day/year = 31,536,000. If we make the very conservative estimate of the number of CPU clock cycles required for testing each key to be 100, then a 1-GHz machine can test approximately 100,000,000 keys per second. This results in 315,360,000,000,000 keys tested per year. This is a lot of keys, but unfortunately, 2^128 keys will then take 1,079,028,307,080,601,418,897,052 years to test. The universe is believed to be no older than 15 billion years, so the brute-force attack on this cipher would take 71,935,220,472,040 times as long as the age of the universe. Current semiconductor technology is not all that far from the theoretical switching-speed limits imposed on us by quantum mechanics, [25] so we cannot hope to get enough relief by waiting for improved clock speeds.
Trying to solve the problem by distributing the attack over multiple machines is also quite futile. To complete the attack in one year, assuming that you could achieve perfect scalability, you would need to purchase 1,079,028,307,080,601,418,897,052 CPUs. Even at volume discounts , this will cost much more than the entire annual global economy of planet earth. The volume of the moon is approximately 2.2 * 10^25 cubic centimeters. Assuming 1 cubic centimeter per CPU, your custom-built supercomputer would occupy about 5 percent of the volume of the moon. But that is only the volume of the CPUs. The memory and bus interconnect hardware would be the 3D mother of all motherboards, which would easily fill another 20 percent of the moon's volume. This would create enough gravitational force to crush the devices at the center of the computer and would create an enormous list of other moon- sized problems. The questions become absurd: How much would it cost? How long would it take to build? How would we program it? How much power would it consume ? Obviously, these are all silly questions, but they do clearly demonstrate that the brute-force key-search attack has its limitations if the key space is large enough. If you would like to see a program that makes these monstrous calculations, see the C# program example BigIntegerFun . The current release of the .NET Framework does not yet support multiprecision arithmetic, so this example is written using GnuMP, [26] which is an open and free software library written in C for arbitrary precision-integer arithmetic, available at www.gnu.org.
Arbitrary Precision ArithmeticCryptography ( especially asymmetric cryptography, described in Chapter 4) often involves the heavy use of arbitrary precision arithmetic. You may never need to use these specialized math capabilities directly. This is because the .NET Framework provides a thorough implementation of most of the cryptographic functionality that you are likely to need. However, there may be situations now and then where you would like to invoke these advanced arithmetic capabilities directly, which would require the use of a specialized math library, such as GnuMP. This can be particularly true if you begin experimenting with your own asymmetric cryptographic algorithm designs. In that case, see Appendix C to see how you can download and install the GnuMP library and use it in your own .NET programs. |
EAN: 2147483647
Pages: 126




 symbol. In C# this operator is represented with the ^ symbol. Once used, the key is never used for encryption again. It should be recognized that the XOR operator is its own inverse, meaning that
symbol. In C# this operator is represented with the ^ symbol. Once used, the key is never used for encryption again. It should be recognized that the XOR operator is its own inverse, meaning that