Binary Numbers

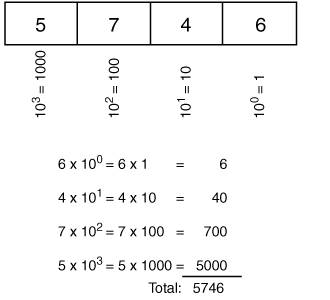
Decimal Numbers

We first analyze the decimal numbers that we are familiar with. Decimal numbers are known as base 10 numbers. Within all numbering systems, the symbols used as digits range from 0 up to one less than the base; thus, within decimal numbers, the following ten unique symbols are used as digits:

0 1 2 3 4 5 6 7 8 9

When multiples of these symbols are combined to create a decimal number, each digit in the number is weighted based on its position within the number. The weights used are all powers of 10 (which is what base 10 means). The rightmost digit, which is the least significant, has a weight of 10⁰ (1). The next digit has a weight of 10¹ (10). The next has a weight of 10² (100), and so on.

For example, consider the decimal number 5746. Figure C-1 illustrates how this number is interpreted.

Figure C-1. Interpreting a Decimal Number

Figure C-1 describes the following points:

• The least significant digit, 6, has a weight of 10⁰; thus, it represents 6 * 10⁰ = 6 * 1 = 6.

• The next digit, 4, has a weight of 10¹; thus, it represents 4 * 10¹ = 4 * 10 = 40.

• The next digit, 7, has a weight of 10²; thus it represents 7 * 10² = 7 * 100 = 700.

• The most significant digit, 5, has a weight of 10³; thus, it represents 5 * 10³ = 5 * 1000 = 5000.

• The decimal number is the sum of these representations: 5000 + 700 + 40 + 6 = 5746.

We read this number as "five thousand seven hundred and forty-six."

The next section provides a similar analysis of binary numbers.