1.4 Note on empirical estimation of the market risk premium
1.4 Note on empirical estimation of the market risk premium
Empirical testing and application of this model requires the specification of three parameters: the instantaneous drift v and instantaneous variance s of the short- term interest rate process as well as the market price of risk q .Since v and s are parameters of the observable short-term interest rate process, they can be obtained by statistical analysis of market data. As previously mentioned, the market risk premium is not directly observable. Although it may be calculated from equation (1.12) as q ( r , t )=( ¼ ( t , T ) ˆ’ r ( t ))/ ƒ ( t , T ), a more direct method of estimation may be applied. Once v and s are determined, the market risk premium may be estimated from the slope of the yield curve at the origin. From equation (1.18) we have P as a function of T and z ( T ) and hence:
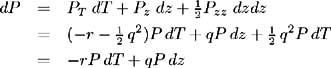
Therefore ![]() and
and ![]() . Also:
. Also:
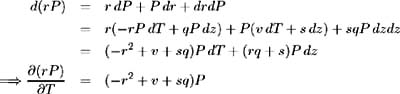
and hence
so
However, from equation (1.1) we have:

Equating to (1.19) we have:
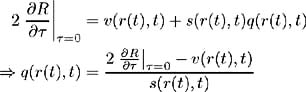
and hence we have found the market price of risk in terms of the slope of the term structure at the origin.
EAN: 2147483647
Pages: 132