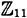Cryptography: Theory and Practice:Other Public-key Cryptosystems | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

Thus E has 13 points on it. Since any group of prime order is cyclic, it follows that E is isomorphic to 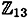, and any point other than the point at infinity is a generator of E. Suppose we take the generator α = (2, 7). Then we can compute the

**Table 5.2** Points on the elliptic curve y² = x³ + x + 6 over
x	x³+x+6 mod 11	in QR(11)?	y
0 1 2 3 4 5 6 7 8 9 10	6 8 5 3 8 4 8 4 9 7 4	no no yes yes no yes no yes yes no yes	4,7 5,6 2,9 2,9 3,8 2, 9

“powers” of α (which we will write as multiples of α, since the group operation is additive). To compute 2α = (2, 7) + (2, 7), we first compute

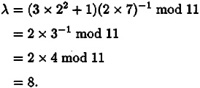
Then we have

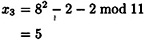
and

so 2α (5, 2).

The next multiple would be 3α = 2α + α = (5, 2) + (2, 7). Again, we begin by computing λ, which in this situation is done as follows:

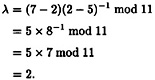
Then we have

and

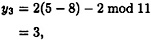
so 3α = (8, 3).

Continuing in this fashion, the remaining multiples can be computed to be the following:

α	=	(2,7)	2α	=	(5,2)	3α	=	(8,3)
4α	=	(10,2)	5α	=	(3,6)	6α	=	(7,9)
7α	=	(7,2)	8α	=	(3,5)	9α	=	(10,9)
10α	=	(8,8)	11α	=	(5,9)	12α	=	(2, 4)

Hence α = (2.7) is indeed a primitive element.

An elliptic curve E defined over (p prime, p > 3) will have roughly p points on it. More precisely, a well-known theorem due to Hasse asserts that the number of points on E, which we denote by #E, satisfies the following inequality

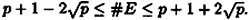
Computing the exact value of #E is more difficult, but there is an efficient algorithm to do this, due to Schoof. (By “efficient” we mean that it has a running time that is polynomial in log p. School’s algorithm has a running time of O((log p)⁸) bit operations and is practical for primes p having several hundred digits.)

Now, given that we can compute #E, we further want to find a cyclic subgroup of E in which the discrete log problem is intractible. So we would like to know something about the structure of the group E. The following theorem gives a considerable amount of information on the group structure of E.

THEOREM 5.1

Let E be an elliptic curve defined over 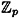, where p is prime, p > 3. Then there exist integers n1 and n2 such that E is isomorphic to 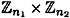. Further, n₂ | n₁ and n₂ | (p - 1).

Hence, if the integers n₁ and n₂ can be computed, then we know that E has a cyclic subgroup isomorphic to 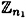that can potentially be used as a setting tot an ElGamal Cryptosystem.

Note that if n₂ = 1, then E is a cyclic group. Also, if #E is a prime, or the product of distinct primes, then E must be a cyclic group.

The Shanks and Pohlig-Hellman algorithms apply to the elliptic curve logarithm problem, but there is no known adaptation of the index calculus method to elliptic curves. However, there is a method of exploiting an explicit isomorphism between elliptic curves and finite fields that leads to efficient algorithms for certain classes of elliptic curves. This technique, due to Menezes, Okamoto and Vanstone, can be applied to some particular examples within a special class of elliptic curves called supersingular curves that were suggested for use in cryptosystems. If the supersingular curves are avoided, however, then it appears that an elliptic curve having a cyclic subgroup of size about 2¹⁶⁰ will provide a secure setting for a cryptosystem, provided that the order of the subgroup is divisible by at least one large prime factor (again, to guard against a Pohlig-Hellman attack).

Let’s now look at an example of ElGamal encryption using the elliptic curve of Example 5.7.

Example 5.8

Suppose that α = (2, 7) and Bob’s secret “exponent” is a = 7, so

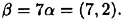
Thus the encryption operaton is

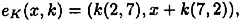
where x ∈ E and 0 ≤ k ≤ 12, and the decryption operation is

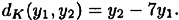
Suppose that Alice wishes to encrypt the message x = (10, 9) (which is a point on E). If she chooses the random value k = 3, then she will compute

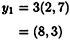
and

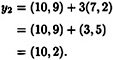
Hence, y = ((8, 3), (10, 2)). Now, if Bob receives the ciphertext y, he decrypts it as follows:

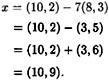
Hence, the decryption yields the correct plaintext.

There are some practical difficulties in implementing an ElGamal Cryptosystem on an elliptic curve. This system, when implemented in 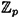(or in GF(pⁿ) with n > 1) has a message expansion factor of two. An elliptic curve implementation has a message expansion factor of (about) four. This happens since there are approximately p plaintexts, but each ciphertext consists of four field elements. A more serious problem is that the plaintext space consists of the points on the curve E, and there is no convenient method known of deterministically generating points on E.

Table of Contents