Cryptography: Theory and Practice:The RSA System and Factoring | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

4.2.3 Other Useful Facts

We next mention another result from elementary group theory, called Lagrange’s Theorem, that will be relevant in our treatment of the RSA Cryptosystem. For a (finite) multiplicative group G, define the order of an element g ∈ G to be the smallest positive integer m such that g^m = 1. The following result is fairly simple, but we will not prove it here.

THEOREM 4.4 (Lagrange)

Suppose G is a multiplicative group of order n, and g∈ G. Then the order of g divides n.

For our purposes, the following corollaries are essential.

COROLLARY 4.5

If 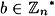, then b^φ(n) ≡ 1 (mod n).

PROOF 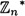is a multiplicative group of order φ(n).

COROLLARY 4.6 (Fermat)

Suppose p is prime and 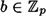. Then b^p ≡ b (mod p).

PROOF If p is prime, then φ(p) = p - 1. So, for 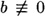(mod p), the result follows from Corollary 4.5. For b ≡ 0 (mod p), the result is also true since 0^p ≡ 0 (mod p).

At this point, we know that if p is prime, then 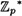is a group of order p - 1, and any element in 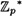has order dividing p - 1. However, if p is prime, then the group is in fact cyclic: there exists an element 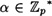having order equal to p - 1. We will not prove this very important fact, but we do record it for future reference:

THEOREM 4.7

If p is prime, then 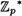is a cyclic group.

An element α having order p - 1 is called a primitive element modulo p. Observe that α is a primitive element if and only if

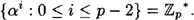
Now, suppose p is prime and α is a primitive element modulo p. Any element 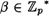can be written as β = αⁱ, where 0 ≤ i ≤ p - 2, in a unique way. It is not difficult to prove that the order of β = αⁱ is

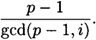
Thus β is itself a primitive element if and only if gcd(p - 1, i) = 1. It follows that the number of primitive elements modulo p is φ(p - 1).

Example 4.4

Suppose p = 13. By computing successive powers of 2, we can verify that 2 is a primitive element modulo 13:

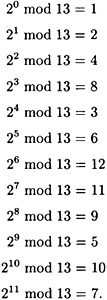
The element 2ⁱ is primitive if and only if gcd(i, 12) = 1; i.e., if and only if i = 1, 5, 7 or 11. Hence, the primitive elements modulo 13 are 2, 6, 7 and 11.

Figure 4.2 RSA Cryptosystem

4.3 The RSA Cryptosystem

We can now describe the RSA Cryptosystem. This cryptosystem uses computations in 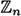, where n is the product of two distinct odd primes p and q. For such n, note that φ(n) = (p - 1) (q - 1).

The formal description of the cryptosystem is given in Figure 4.2. Let’s verify that encryption and decryption are inverse operations. Since

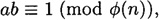
we have that

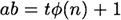
for some integer t ≥ 1. Suppose that ; then we have

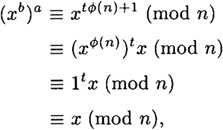
as desired. We leave it as an exercise for the reader to show that (x^b)^a ≡ x (mod n) if

Here is a small (insecure) example of the RSA Cryptosystem.

Example 4.5

Suppose Bob chooses p = 101 and q = 113. Then n = 11413 and φ(n) = 100 × 112 = 11200. Since 11200 = 2⁶5²7, an integer b can be used as an encryption exponent if and only if b is not divisible by 2, 5 or 7. (In practice, however, Bob will not factor φ(n). He will verify that gcd(φ(n), b) = 1 using the Euclidean algorithm.) Suppose Bob chooses b = 3533. Then the Extended Euclidean algorithm will yield

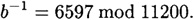
Hence, Bob’s secret decryption exponent is a = 6597.

Bob publishes n = 11413 and b = 3533 in a directory. Now, suppose Alice wants to send the plaintext 9726 to Bob. She will compute

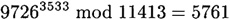
and send the ciphertext 5761 over the channel. When Bob receives the ciphertext 5761, he uses his secret decryption exponent to compute

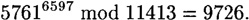
(At this point, the encryption and decryption operations might appear to be very complicated, but we will discuss efficient algorithms for these operations in the next section.)

The security of RSA is based on the hope that the encryption function e_K (x) = x^b mod n is one-way, so it will be computationally infeasible for an opponent to decrypt a ciphertext. The trapdoor that allows Bob to decrypt is the knowledge of the factorization n = pq. Since Bob knows this factorization, he can compute φ(n) = (p - 1)(q - 1) and then compute the decryption exponent a using the Extended Euclidean algorithm. We will say more about the security of RSA later on.

Table of Contents