Cryptography: Theory and Practice:Shannon s Theory | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

2.3 Properties of Entropy

In this section, we prove some fundamental results concerning entropy. First, we state a fundamental result, known as Jensen’s Inequality, that will be very useful to us. Jensen’s Inequality involves concave functions, which we now define.

DEFINITION 2.4 A real-valued function f is concave on an interval I if

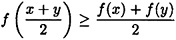
for all x, y ∈ I. f is strictly concave on an interval I if

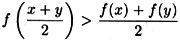
for all x, y ∈ I, x ≠ y.

Here is Jensen’s Inequality, which we state without proof.

THEOREM 2.5 (Jensen’s Inequality)

Suppose f is a continuous strictly concave function on the interval I,

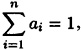
and a_i > 0, 1 ≤ i ≤ n. Then

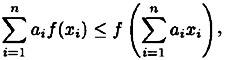
where x_i ∈ I, 1 ≤ i ≤ n. Further, equality occurs if and only if x₁ = ... = x_n.

We now proceed to derive several results on entropy. In the next theorem, we make use of the fact that the function log₂ x is strictly concave on the interval (0, ∞). (In fact, this follows easily from elementary calculus since the second deriviative of the logarithm function is negative on the interval (0, ∞).)

THEOREM 2.6

Suppose X is a random variable having probability distribution p₁, p₂, p_n, where p_i > 0, 1 ≤ i ≤ n. Then H(X) ≤ log₂ n, with equality if and only if p_i = 1/n, 1 ≤ i ≤ n.

PROOF Applying Jensen’s Inequality, we have the following:

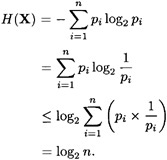
Further, equality occurs if and only if p_i = 1/n, 1 ≤ i ≤ n.

THEOREM 2.7

H (X, Y) ≤ H(X) + H(Y), with equality if and only if X and Y are independent events.

PROOF Suppose X takes on values x_i, 1 ≤ i ≤ m, and Y takes on values y_j, 1 ≤ j ≤ n. Denote p_i = p(X = x_i), 1 ≤ i ≤ m, and q_j = p(Y = y_j), 1 ≤ j ≤ n. Denote r_ij = p(X = x_i, Y = y_j), 1 ≤ i ≤ m, 1 ≤ j ≤ n (this is the joint probability distribution).

Observe that

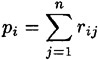
(1 ≤ i ≤ m) and

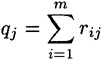
(1 ≤ j ≤ n). We compute as follows:

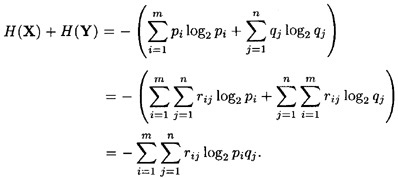
On the other hand,

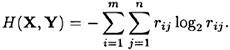
Combining, we obtain the following:

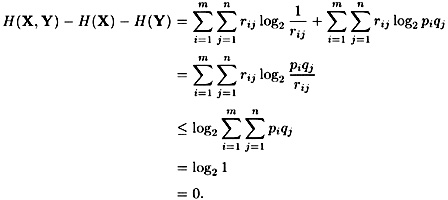
(Here, we apply Jensen’s Inequality, using the fact that the r_ij’s form a probability distribution.)

We can also say when equality occurs: it must be the case that there is a constant c such that p_iq_j/r_ij = c for all i, j. Using the fact that

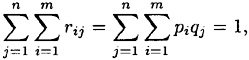
it follows that c = 1. Hence, equality occurs if and only if r_ij = p_iq_j, i.e., if and only if

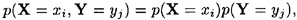
1 ≤ i ≤ m, 1 ≤ j ≤ n. But this says that X and Y are independent.

We next define the idea of conditional entropy.

DEFINITION 2.5 Suppose X and Y are two random variables. Then for any fixed value y of Y, we get a (conditional) probability distribution p(X|y). Clearly,

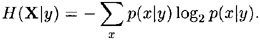
We define the conditional entropy H(X|Y) to be the weighted average (with respect to the probabilities p(y)) of the entropies H(X|y) over all possible values y. It is computed to be

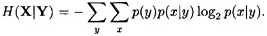
The conditional entropy measures the average amount of information about X that is revealed by Y.

The next two results are straightforward; we leave the proofs as exercises.

THEOREM 2.8

H(X, Y) = H(Y) + H(X|Y).

COROLLARY 2.9

H(X|Y) ≤ H(X), with equality if and only if X and Y are independent.

Table of Contents